
科目:gzsx 来源: 题型:
| x |
|
科目:gzsx 来源: 题型:填空题
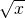 ,|x-2|},其中min{a,b}=
,|x-2|},其中min{a,b}=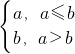 ,若动直线y=m与函数y=f(x)f(x)的图象有三个不同的交点,它们的横坐标分别为x1,x2,x3,则x1•x2•x3是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”________.
,若动直线y=m与函数y=f(x)f(x)的图象有三个不同的交点,它们的横坐标分别为x1,x2,x3,则x1•x2•x3是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”________.科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
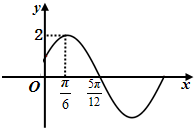 (理)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
(理)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π | 2 |
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
| 1 | 2 |
科目:gzsx 来源: 题型:
| b |
| x |
| 1 |
| an-n+1 |
科目:gzsx 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
科目:gzsx 来源: 题型:
| 1 |
| 4a |
| 1 |
| 2 |
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
| x-5 | x+5 |
科目:gzsx 来源: 题型:
| 1 |
| x |
| a |
| x |