科目：gzsx 来源： 题型：
A.4 B.3 C.2 D.1
科目：gzsx 来源：2010年大连市高二六月月考理科数学卷 题型：解答题
（本小题满分12分）
已知函数f(x)=x3+bx2+cx+d (b,c,d∈R且都为常数)的导函数f¢(x)=3x2+4x且f(1)=7，设F(x)=f(x)-ax2
(1)当a<2时，求F(x)的极小值；
(2)若对任意x∈[0,+∞)都有F(x)≥0成立，求a的取值范围；
(3)在(2)的条件下比较a2-13a+39与的大小.
科目：gzsx 来源： 题型：013
设f(x)=ax3+bx2+cx+d在x=1处有极大值1，在x=2处有极小值0．则常数a，b，c，d分别为（ ）
A．
，
，0，1 B．
，
，0，1
C．
，
，0，-1 D．
，
，0，1
科目：gzsx 来源：成功之路·突破重点线·数学（学生用书） 题型：013
设f(x)＝ax3＋bx2＋cx＋d的图象如下图，则b属于
[ ]
A．(－∞，0)
B．(0，1)
C．(1，2)
D．[2，＋∞)
科目：gzsx 来源： 题型：
处取得最小值
.设F(x)=f(x)-ax2(a∈R).(1)当a＜2时,求F(x)的极小值;
(2)已知P:x∈［0,+∞),Q:F(x)≥0,若P为Q的充分条件,求实数a的取值范围.
科目：gzsx 来源：天利38套《2008全国各省市高考模拟试题汇编(大纲版)》、数学文 大纲版 题型：044
已知函数f(x)＝x3＋bx2＋cx＋d(b、c、d∈R且都为常数)的导函数为
，且f(1)＝7，设F(x)＝f(x)－ax2(a∈R)．
(Ⅰ)当a＜2时，求F(x)的极小值；
(Ⅱ)若对任意的x∈[0，＋∞)，都有F(x)≥0成立，求a的取值范围并证明不等式
．
科目：gzsx 来源：2008届第一次六校联考高三数学文科试卷(广州深圳中山珠海惠州) 题型：044
解答时应写出必要的文字说明、证明过程或演算步骤
设函数f(x)＝ax3＋bx2＋cx＋d(a、b、c、d∈R)满足：
都有f(x)＋f(－x)＝0，且x＝1时，f(x)取极小值
(1)f(x)的解析式；
(2)当x∈[－1，1]时，证明：函数图象上任意两点处的切线不可能互相垂直；
(3)设F(x)＝|xf(x)|，证明：
时，
科目：gzsx 来源：数学教研室 题型：013
A．
，
，0，1 B．
，
，0，1
C．
，
，0，-1 D．
，
，0，1
科目：gzsx 来源：聊城一中高三年级阶段性综合测试 题型：013
设f(x)＝3ax－2a＋1，若存在t∈[－1，1]，使f(t)＜0，则实数a的取值范围是
－1＜a＜
a＜－1
a＜－1或a＞
a＞或a≥2
科目：gzsx 来源：2008届高三最后一次模拟考试数学试卷(新课程文科) 题型：044
设函数f(x)＝ax3＋bx2＋cx＋d(a、b、c、d∈R)满足：
都有f(x)＋f(－x)＝0，且x＝1时，f(x)取极小值
(1)f(x)的解析式；
(2)当x∈[－1，1]时，证明：函数图象上任意两点处的切线不可能互相垂直；
(3)设F(x)＝xf(x)，证明：
时，
科目：gzsx 来源： 题型：
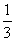(m∈R,e=2.718 28…是自然对数的底数).(1)求函数f(x)的极值;
(2)当x＞0时,设f(x)的反函数为f-1(x),对0＜p＜q,试比较f(q-p)、f-1(q-p)及f-1(q)-f-1(p)的大小.
(文)已知函数f(x)=x3+bx2+cx+d(b、c、d∈R且都为常数)的导函数为f′(x)=3x2+4x,且f(1)=7,设F(x)=f(x)-ax2(a∈R).
(1)当a＜2时,求F(x)的极小值;
(2)若对任意的x∈［0,+∞),都有F(x)≥0成立,求a的取值范围并证明不等式a2-13a+39≥
.
科目：gzsx 来源：山东省济宁市梁山二中2011－2012学年高一上学期期中考试数学试题 题型：044
设f(x)＝3x，且f(a＋2)＝18，g(x)＝3ax－4x(x∈R)
(1)求g(x)的解析式；
(2)判断g(x)在[0，1]上的单调性并用定义证明；
(3)若方程g(x)－b＝0在[－2，2]上有两个不同的解，求实数b的取值范围．
科目：gzsx 来源： 题型：
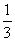(m∈R,e=2.718 28…是自然对数的底数).(1)求函数f(x)的极值;
(2)当x＞0时,设f(x)的反函数为f-1(x),对0＜p＜q,试比较f(q-p)、f-1(q-p)及f-1(q)-f-1(p)的大小.
(文)已知函数f(x)=x3+bx2+cx+d(b、c、d∈R且都为常数)的导函数为f′(x)=3x2+4x,且f(1)=7,设F(x)=f(x)-ax2(a∈R).
(1)当a＜2时,求F(x)的极小值;
(2)若对任意的x∈［0,+∞),都有F(x)≥0成立,求a的取值范围并证明不等式a2-13a+39≥
.
科目：gzsx 来源： 题型：
已知函数f(x)=2x3+ax与g(x)=bx2+c图象都过P(2,0),且在P点有相同切线。
（1）求a,b,c值；
（2）设F(x)=f(x)+g(x)，求F(x)单调区间。
科目：gzsx 来源： 题型：
| MN |
| MP |
| PM |
| PF |
| |AF| |
| |BF| |
| |DF| |
科目：gzsx 来源： 题型：
| a |
| b |
| a |
| b |
| π |
| 2 |
科目：gzsx 来源： 题型：
| a |
| 3 |
| b-1 |
| 2 |
科目：gzsx 来源： 题型：
| ex+e-x |
| 2 |
| ex-e-x |
| 2 |
科目：gzsx 来源： 题型：
| a |
| 3 |
| b |
| a |
| b |
| π |
| 4 |
| π |
| 4 |
| a |
| b |