
科目:gzsx 来源: 题型:
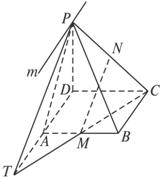
(1)求证:BC∥m;
(2)MN与平面PAD是否平行?试证明你的结论.
科目:gzsx 来源:数学教研室 题型:047
如图,点P为四边形ABCD所在平面外一点,且PA⊥平面ABCD,若AB⊥AD,PA=AD,M为PC中点截面ABMN是平行四边形.
求证:(1)AB∥CD;
(2)AN⊥MN;
(3)截面ABMN⊥侧面PCD.

科目:gzsx 来源: 题型:047
如图,点
P为四边形ABCD所在平面外一点,且PA⊥平面ABCD,若AB⊥AD,PA=AD,M为PC中点,截面ABMN是平行四边形.求证:
(1)AB∥CD;(2)AN
⊥MN;(3)
截面ABMN⊥侧面PCD.
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:解答题
 【问题提出】
【问题提出】科目:gzsx 来源: 题型:
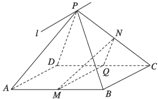 如图所示,P为平行四边形ABCD所在平面外一点,M、N分别为AB、PC的中点,平面PAD∩平面PBC=l.
如图所示,P为平行四边形ABCD所在平面外一点,M、N分别为AB、PC的中点,平面PAD∩平面PBC=l.科目:gzsx 来源:单元双测 同步达标活页试卷 高二数学(下A) 人教版 题型:013
如图所示,P为![]() ABCD所在平面外一点,过BC的平面与PAD交于EF,则四边形EFBC是
ABCD所在平面外一点,过BC的平面与PAD交于EF,则四边形EFBC是

A.空间四边形
B.平面四边形
C.梯形
D.平行四边形
科目:gzsx 来源:黑龙江省实验中学2006-2007学年度上学期期末高二学年数学学科试题(理科) 题型:044
如图:AM是平行四边形ABCD所在平面外的一条线段,P为AM的中点,求证:MC∥面PDB.
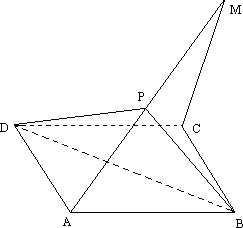
科目:gzsx 来源:黑龙江省实验中学2006-2007学年度上学期期末高二学年数学学科试题(文科) 题型:044
如图:AM是平行四边形ABCD所在平面外的一条线段,P为AM的中点,求证:MC∥面PDB

科目:gzsx 来源:学习高手必修二数学苏教版 苏教版 题型:047
如图所示,P为平行四边形ABCD所在平面外一点,M、N分别为AB、PC的中点,平面PAD∩平面PBC=l.

(1)求证:BC∥l.
(2)MN与平面PAD是否平行,试证明你的结论.
科目:gzsx 来源:2014-2015学年江苏省高邮市高二学情检测数学试卷(解析版) 题型:解答题
如图所示,P为平行四边形ABCD所在平面外一点,M、N分别为AB、PC的中点,平面PAD∩平面PBC=l.

(1)求证:BC∥l;
(2)MN与平面PAD是否平行?试证明你的结论。
科目:gzwl 来源: 题型:计算题
如图所示的平面直角坐标系xOy,在第一象限内有平行于y轴的匀强电场,方向沿y轴负方向;在第四象限的正方形abcd区域内有匀强磁场,方向垂直于xOy平面向外,正方形边长为L,且ab边与y轴平行。一质量为m、电荷量为q的粒子,从y轴上的P(0,h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第四象限,又经过磁场从y轴上的某点进入第三象限,且速度与y轴负方向成45°角,不计粒子所受的重力。求: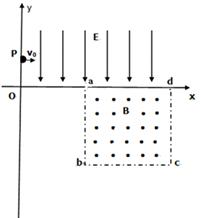
(1)判断粒子带电的电性,并求电场强度E的大小;
(2)粒子到达a点时速度的大小和方向;
(3)abcd区域内磁场的磁感应强度B的最小值。
科目:gzwl 来源:2013-2014学年云南省昭通市高三5月统测理综物理试卷(解析版) 题型:计算题
如图所示的平面直角坐标系xOy,在第一象限内有平行于y轴的匀强电场,方向沿y轴负方向;在第四象限的正方形abcd区域内有匀强磁场,方向垂直于xOy平面向外,正方形边长为L,且ab边与y轴平行。一质量为m、电荷量为q的粒子,从y轴上的P(0,h)点,以大小为v0的速度沿x轴正方向射入电场,通过电场后从x轴上的a(2h,0)点进入第四象限,又经过磁场从y轴上的某点进入第三象限,且速度与y轴负方向成45°角,不计粒子所受的重力。求:
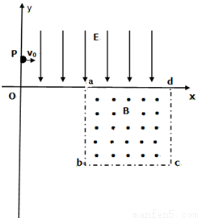
(1)判断粒子带电的电性,并求电场强度E的大小;
(2)粒子到达a点时速度的大小和方向;
(3)abcd区域内磁场的磁感应强度B的最小值。
科目:czsx 来源:2012年青海省中考数学试卷(解析版) 题型:解答题
科目:gzsx 来源: 题型:解答题
 如图,点P为平行四边形ABCD所在平面外一点,点E为PC的中点,在DE上取一点G,过点G和直线AP作平面APG交平面BDE于GH,求证:AP∥GH.
如图,点P为平行四边形ABCD所在平面外一点,点E为PC的中点,在DE上取一点G,过点G和直线AP作平面APG交平面BDE于GH,求证:AP∥GH.