科目:czsx 来源:解题升级 解题快速反应一典通 九年级级数学 题型:044
一个函数的图像是以原点为顶点,y轴为对称轴的抛物线,且过点M(-2,2).(1)求出这个函数的解析式并画出函数图像;(2)写出抛物线上与点M关于y轴的对称点N的坐标,并求出△MON的面积;(3)在抛物线上是否存在一个点P,使得△MNP的面积等于△MON面积的一半?如果存在,求出P点坐标;如果不存在,说明理由.
科目:gzsx 来源:2010年重庆一中高一上学期10月月考数学卷 题型:解答题
已知二次函数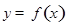 的图像与
的图像与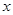 轴交于
轴交于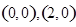 且有最大值为
且有最大值为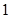 。
。
(1)求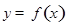 的解析式;
的解析式;
(2)设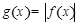 ,画出
,画出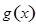 的大致图像,并指出
的大致图像,并指出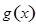 的单调区间;
的单调区间;
(3)若方程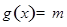 恰有四个不同的解,根据图像指出实数
恰有四个不同的解,根据图像指出实数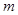 的取值范围。
的取值范围。
科目:gzsx 来源:不详 题型:解答题
 的图像与
的图像与 轴交于
轴交于 且有最大值为
且有最大值为 。
。 的解析式;
的解析式;  ,画出
,画出 的大致图像,并指出
的大致图像,并指出 的单调区间;
的单调区间; 恰有四个不同的解,根据图像指出实数
恰有四个不同的解,根据图像指出实数 的取值范围。
的取值范围。科目:czsx 来源:2013届江苏省江阴暨阳九年级上学期期末考试数学试卷(带解析) 题型:解答题
如图,二次函数 的图像交
的图像交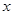 轴于
轴于 ,交
,交 轴于
轴于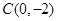 ,过
,过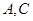 画直线。
画直线。
(1)求二次函数的解析式;
(2)若点P是抛物线上的动点,点Q是直线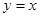 上的动点,请判断是否存在以P、Q、O、C为顶点的四边形为平行四边形,若存在,请求出点Q的坐标;若不存在,请说明理由;
上的动点,请判断是否存在以P、Q、O、C为顶点的四边形为平行四边形,若存在,请求出点Q的坐标;若不存在,请说明理由;
(3)在 轴右侧的点
轴右侧的点 在二次函数图像上,以
在二次函数图像上,以 为圆心的圆与直线
为圆心的圆与直线 相切,切点为
相切,切点为 。且△CHM∽△AOC(点
。且△CHM∽△AOC(点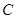 与点
与点 对应),求点
对应),求点 的坐标。
的坐标。
科目:czsx 来源:2012-2013学年江苏省江阴暨阳九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,二次函数 的图像交
的图像交 轴于
轴于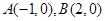 ,交
,交 轴于
轴于 ,过
,过 画直线。
画直线。
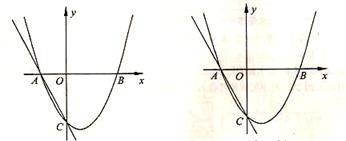
(1)求二次函数的解析式;
(2)若点P是抛物线上的动点,点Q是直线 上的动点,请判断是否存在以P、Q、O、C为顶点的四边形为平行四边形,若存在,请求出点Q的坐标;若不存在,请说明理由;
上的动点,请判断是否存在以P、Q、O、C为顶点的四边形为平行四边形,若存在,请求出点Q的坐标;若不存在,请说明理由;
(3)在 轴右侧的点
轴右侧的点 在二次函数图像上,以
在二次函数图像上,以 为圆心的圆与直线
为圆心的圆与直线 相切,切点为
相切,切点为 。且△CHM∽△AOC(点
。且△CHM∽△AOC(点 与点
与点 对应),求点
对应),求点 的坐标。
的坐标。
科目:czsx 来源:不详 题型:解答题
 的图像交
的图像交 轴于
轴于 ,交
,交 轴于
轴于 ,过
,过 画直线。
画直线。
 上的动点,请判断是否存在以P、Q、O、C为顶点的四边形为平行四边形,若存在,请求出点Q的坐标;若不存在,请说明理由;
上的动点,请判断是否存在以P、Q、O、C为顶点的四边形为平行四边形,若存在,请求出点Q的坐标;若不存在,请说明理由; 轴右侧的点
轴右侧的点 在二次函数图像上,以
在二次函数图像上,以 为圆心的圆与直线
为圆心的圆与直线 相切,切点为
相切,切点为 。且△CHM∽△AOC(点
。且△CHM∽△AOC(点 与点
与点 对应),求点
对应),求点 的坐标。
的坐标。科目:czsx 来源:期中题 题型:解答题
 的图像与一次函数
的图像与一次函数 的图像相交于A(2,1)。
的图像相交于A(2,1)。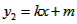 的图像上,若在请求出S△APQ;若不在,请求出直线AQ的解析式;
的图像上,若在请求出S△APQ;若不在,请求出直线AQ的解析式; ;②当x取何值时,
;②当x取何值时, 。
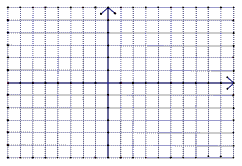
。
科目:czsx 来源: 题型:
知识迁移
我们知道,函数 的图像是由二次函数
的图像是由二次函数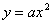 的图像向右平移m个单位,再向上平移n个单位得到.类似地,函数
的图像向右平移m个单位,再向上平移n个单位得到.类似地,函数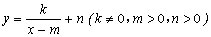 的图像是由反比例函数
的图像是由反比例函数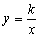 的图像向右平移m个单位,再向上平移n个单位得到,其对称中心坐标为(m,n).
的图像向右平移m个单位,再向上平移n个单位得到,其对称中心坐标为(m,n).
理解应用
函数 的图像可以由函数
的图像可以由函数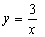 的图像向右平移 个单位,再向上平移 个单位得到,其对称中心坐标为 .
的图像向右平移 个单位,再向上平移 个单位得到,其对称中心坐标为 .
灵活运用
如图,在平面直角坐标系xOy中,请根据所给的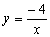 的图像画出函数
的图像画出函数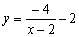 的图像,并根据该图像指出,当x在什么范围内变化时,
的图像,并根据该图像指出,当x在什么范围内变化时,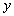 ≥
≥ ?
?

实际应用
某老师对一位学生的学习情况进行跟踪研究.假设刚学完新知识时的记忆存留量为1.新知识学习后经过的时间为x,发现该生的记忆存留量随x变化的函数关系为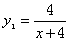 ;若在
;若在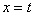 (
(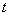 ≥4)时进行一次复习,发现他复习后的记忆存留量是复习前的2倍(复习时间忽略不计),且复习后的记忆存量随x变化的函数关系为
≥4)时进行一次复习,发现他复习后的记忆存留量是复习前的2倍(复习时间忽略不计),且复习后的记忆存量随x变化的函数关系为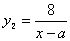 .如果记忆存留量为
.如果记忆存留量为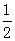 时是复习的“最佳时机点”,且他第一次复习是在“最佳时机点”进行的,那么当x为何值时,是他第二次复习的“最佳时机点”?
时是复习的“最佳时机点”,且他第一次复习是在“最佳时机点”进行的,那么当x为何值时,是他第二次复习的“最佳时机点”?
科目:czsx 来源:2015年初中毕业升学考试(江苏盐城卷)数学(解析版) 题型:解答题
(本题满分12分)知识迁移
我们知道,函数 的图像是由二次函数
的图像是由二次函数 的图像向右平移m个单位,再向上平移n个单位得到.类似地,函数
的图像向右平移m个单位,再向上平移n个单位得到.类似地,函数 的图像是由反比例函数
的图像是由反比例函数 的图像向右平移m个单位,再向上平移n个单位得到,其对称中心坐标为(m,n).
的图像向右平移m个单位,再向上平移n个单位得到,其对称中心坐标为(m,n).
理解应用
函数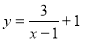 的图像可以由函数
的图像可以由函数 的图像向右平移 个单位,再向上平移 个单位得到,其对称中心坐标为 .
的图像向右平移 个单位,再向上平移 个单位得到,其对称中心坐标为 .
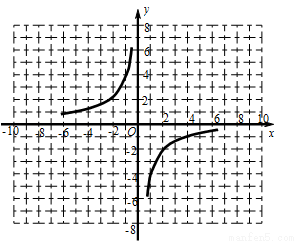
灵活运用
如图,在平面直角坐标系xOy中,请根据所给的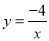 的图像画出函数
的图像画出函数 的图像,并根据该图像指出,当x在什么范围内变化时,
的图像,并根据该图像指出,当x在什么范围内变化时, ≥
≥ ?
?
实际应用
某老师对一位学生的学习情况进行跟踪研究.假设刚学完新知识时的记忆存留量为1.新知识学习后经过的时间为x,发现该生的记忆存留量随x变化的函数关系为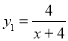 ;若在
;若在 (
( ≥4)时进行一次复习,发现他复习后的记忆存留量是复习前的2倍(复习时间忽略不计),且复习后的记忆存量随x变化的函数关系为
≥4)时进行一次复习,发现他复习后的记忆存留量是复习前的2倍(复习时间忽略不计),且复习后的记忆存量随x变化的函数关系为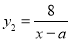 .如果记忆存留量为
.如果记忆存留量为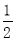 时是复习的“最佳时机点”,且他第一次复习是在“最佳时机点”进行的,那么当x为何值时,是他第二次复习的“最佳时机点”?
时是复习的“最佳时机点”,且他第一次复习是在“最佳时机点”进行的,那么当x为何值时,是他第二次复习的“最佳时机点”?
科目:gzsx 来源:2010年高考试题(新课标全国卷)解析版(理) 题型:填空题
查看答案和解析>>科目:gzsx 来源: 题型:
在已给的坐标系中,画出同时满足下列条件的一个函数![]() 的图像,
的图像,
①![]() 的定义域是[-2,2];②
的定义域是[-2,2];②![]() 是奇函数;③
是奇函数;③![]() 在
在![]() 上是减函数;
上是减函数;
 ④
④![]() 既有最大值,又有最小值;
既有最大值,又有最小值;
⑤![]() ;
;
⑥![]() 不存在反函数.
不存在反函数.
科目:gzsx 来源: 题型:解答题
已知函数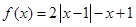 .
.
(1)请在所给的平面直角坐标系中画出函数 的图像;
的图像;
(2)根据函数 的图像回答下列问题:
的图像回答下列问题:
①求函数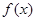 的单调区间;
的单调区间;
②求函数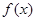 的值域;
的值域;
③求关于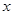 的方程
的方程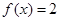 在区间
在区间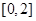 上解的个数.
上解的个数.
(回答上述3个小题都只需直接写出结果,不需给出演算步骤)
科目:gzsx 来源:不详 题型:解答题
 .
.
 的图像;
的图像; 的图像回答下列问题:
的图像回答下列问题: 的单调区间;
的单调区间; 的值域;
的值域; 的方程
的方程 在区间
在区间 上解的个数.
上解的个数.科目:gzsx 来源:2016届江苏省宿迁市高一上学期第二次月考数学试卷(解析版) 题型:解答题
已知函数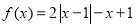 .
.
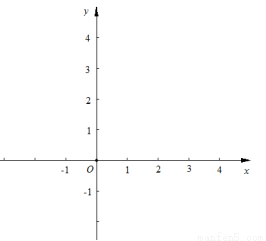
(1)请在所给的平面直角坐标系中画出函数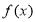 的图像;
的图像;
(2)根据函数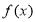 的图像回答下列问题:
的图像回答下列问题:
① 求函数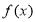 的单调区间;
的单调区间;
② 求函数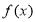 的值域;
的值域;
③ 求关于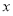 的方程
的方程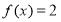 在区间
在区间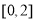 上解的个数.
上解的个数.
(回答上述3个小题都只需直接写出结果,不需给出演算步骤)
科目:gzsx 来源:2014届江西省高一第二次月考数学试卷 题型:解答题
设f(x)=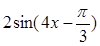
(1)将函数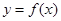 的图象向左平移
的图象向左平移 个单位后,再将得到的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数 的图象,求
的图象,求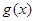 .并用“五点法”画出y=g(x), x∈[0,π]的图像。
.并用“五点法”画出y=g(x), x∈[0,π]的图像。
(2)若关于x的方程g(x)= k+1在 内有两个不同根α、β,求α+β的值及k的取值范围.
内有两个不同根α、β,求α+β的值及k的取值范围.
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|