如图.在△ABC中.∠A.∠B.∠C的对边分别为a.b.c答案解析
科目:gzsx
来源:
题型:解答题
6.课本上的探索与研究中有这样一个问题:
已知△ABC的面积为S,外接圆的半径为R,∠A,∠B,∠C的对边分别为a,b,c,用解析几何的方法证明:$R=\frac{abc}{4S}$.
小东根据学习解析几何的经验,按以下步骤进行了探究:
(1)在△ABC所在的平面内,建立直角坐标系,使得△ABC三个顶点的坐标的表示形式较为简单,并设出表示它们坐标的字母;
(2)用表示△ABC三个顶点坐标的字母来表示△ABC的外接圆半径、△ABC的三边和面积;
(3)根据上面得到的表达式,消去表示△ABC的三个顶点的坐标的字母,得出关系式.
在探究过程中,小东遇到了以下问题,请你帮助完成:
(Ⅰ)为了△ABC的三边和面积表达式及外接圆方程尽量简单,小东考虑了如下两种建系方式;你选择第①种建系方式.
(Ⅱ)根据你选择的建系方式,完成以下部分探究过程:
(1)设△ABC的外接圆的一般式方程为x
2+y
2+Dx+Ey+F=0;
(2)在求解圆的方程的系数时,小东观察图形发现,由圆的几何性质,可以求出圆心的横坐标为$\frac{m+n}{2}$,进而可以求出D=-m-n;
(3)外接圆的方程为x
2+y
2+(-m-n)x+(-p-$\frac{mn}{p}$)y+mn=0.

查看答案和解析>>
科目:gzsx
来源:
题型:
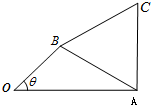
在△ABC中,a,b,c分别为内角A,B,C所对的边,且满足
=.
(1)证明:b+c=2a;
(2)如图,点O是△ABC外一点,设∠AOB=θ(0<θ<π),OA=2OB=2,当b=c时,求平面四边形OACB面积的最大值.
查看答案和解析>>
科目:czsx
来源:
题型:
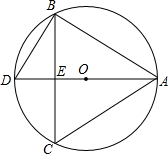
在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程ax
2+bx-c=0为“△ABC的☆方程”.根据规定解答下列问题:
(1)“△ABC的☆方程”ax
2+bx-c=0的根的情况是
②
②
(填序号):①有两个相等的实数根;②有两个不相等的实数根;③没有实数根;
(2)如图,AD为⊙O的直径,BC为弦,BC⊥AD于E,∠DBC=30°,求“△ABC的☆方程”ax
2+bx-c=0的解;
(3)若
x=c是“△ABC的☆方程”ax
2+bx-c=0的一个根,其中a,b,c均为整数,且ac-4b<0,求方程的另一个根.
查看答案和解析>>
科目:czsx
来源:
题型:
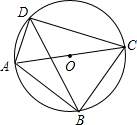
在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程ax
2-bx-c=0为“△ABC的☆方程”.根据规定解答下列问题:
(1)“△ABC的☆方程”ax
2-bx-c=0的根的情况是
(填序号);
①有两个相等的实数根; ②有两个不相等的实数根; ③没有实数根.
(2)如图,AC为⊙O的直径,点D为⊙O上的一点,∠ADC的平分线交⊙O于点B,求“△ABC的☆方程”ax
2-bx-c=0的解;
(3)若x=-
c是“△ABC的☆方程”ax
2-bx-c=0的一个根,其中a,b,c均为正整数,且ac-4b<0,求①求b的值;②求“△ABC的☆方程”的另一个根.
查看答案和解析>>
科目:czsx
来源:2016届江苏省扬中市九年级上学期期中考试数学试卷(解析版)
题型:解答题
在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程 为“△ABC的☆方程”.根据规定解答下列问题:
为“△ABC的☆方程”.根据规定解答下列问题:
(1)“△ABC的☆方程”  的根的情况是______(填序号):
的根的情况是______(填序号):
①有两个相等的实数根;②有两个不相等的实数根;③没有实数根;
(2)如图,AD为⊙O的直径,BC为弦, BC⊥AD于E,∠DBC=30°,求“△ABC的☆方程”  的解;
的解;

(3)若x= 是“△ABC的☆方程”
是“△ABC的☆方程”  的一个根,其中a,b,c均为整数,且
的一个根,其中a,b,c均为整数,且 ,求方程的另一个根.
,求方程的另一个根.
查看答案和解析>>
科目:czsx
来源:
题型:
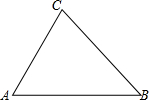
如图,在△ABC中,a,b,c分别为∠A,∠B,∠C的对边.
(1)已知b=6,c=8,∠A=60°,求a的值;
(2)一般地,在三角形中,已知两边及其夹角可以利用公式求出第三边的长,现请你探索已知b,c,A,求a的计算公式,并就△ABC为锐角三角形这一情况,证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
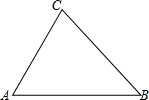 如图,在△ABC中,a,b,c分别为∠A,∠B,∠C的对边.
如图,在△ABC中,a,b,c分别为∠A,∠B,∠C的对边.
(1)已知b=6,c=8,∠A=60°,求a的值;
(2)一般地,在三角形中,已知两边及其夹角可以利用公式求出第三边的长,现请你探索已知b,c,A,求a的计算公式,并就△ABC为锐角三角形这一情况,证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,在△ABC中,a、b、c分别为∠A、∠B、∠C的对边,且2b<a+c,求证:2∠B<∠A+∠C.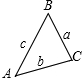
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,在△ABC中,a、b、c分别为∠A、∠B、∠C的对边,且2b<a+c,求证:2∠B<∠A+∠C.

查看答案和解析>>
科目:czsx
来源:2007年福建省福州一中高中招生(面向福州以外)综合素质测试数学试卷(解析版)
题型:解答题
如图,在△ABC中,a,b,c分别为∠A,∠B,∠C的对边.
(1)已知b=6,c=8,∠A=60°,求a的值;
(2)一般地,在三角形中,已知两边及其夹角可以利用公式求出第三边的长,现请你探索已知b,c,A,求a的计算公式,并就△ABC为锐角三角形这一情况,证明你的结论.

查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,在△ABC中,a,b,c分别为∠A,∠B,∠C的对边.
(1)已知b=6,c=8,∠A=60°,求a的值;
(2)一般地,在三角形中,已知两边及其夹角可以利用公式求出第三边的长,现请你探索已知b,c,A,求a的计算公式,并就△ABC为锐角三角形这一情况,证明你的结论.

查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数y=f(x)的图象是由y=sinx图象经过如下三个步骤变化得到的:
①将y=sinx的图象的纵坐标不变,横坐标缩短为原来的
;
②将①中图象整体向左平移
个单位;
③将②中的图象的横坐标不变,纵坐标伸长为原来的2倍.
(I)求f(x)的单调递增区间;
(Ⅱ)在△ABC中,a、b、c分别为角A、B、C的对边,若f(A)=
,a=
,b+c=
,求△ABC面积.
查看答案和解析>>
科目:czsx
来源:
题型:

9、如图,在△ABC中,a、b、c分别为∠A、∠B、∠C的对边,且2b<a+c,求证:2∠B<∠A+∠C.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在△ABC中,∠BAC、∠B、∠C的对边分别为a、b、c,且(ab-1)
2+(a-b)
2=0.
(l)求证:AC=BC.
(2)作△ABC的角平分线AD,若AC+CD=AB,求S
△ABC.
查看答案和解析>>
科目:czsx
来源:数学教研室
题型:013
如图,在△ABC中,∠A=90°,∠A,∠B,∠C的对边分别为a,b,c.则下列结论不正确的是
[ ]

查看答案和解析>>
科目:czsx
来源:
题型:013
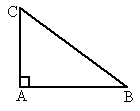
如图,在△ABC中,∠A=90°,∠A,∠B,∠C的对边分别为a,b,c.则下列结论不正确的是
[ ]
查看答案和解析>>
科目:czsx
来源:
题型:
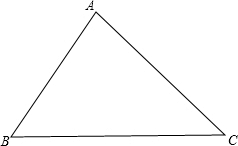
如图,在△ABC中,∠A=2∠C,∠A,∠B,∠C的对边分别为a、b、c,试探究a、b、c之间的关系.
查看答案和解析>>
科目:czsx
来源:
题型:
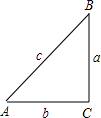
如图,在△ABC中,∠C=90°,角A、B、C的对边分别为a、b、c,设△ABC的面积为s,周长的一半为l.
(1)填写表:
| 三边a、b、c |
l-a |
l-b |
s |
| 3、4、5 |
3 |
2 |
6 |
| 5、12、13 |
|
|
|
| 8、15、17 |
|
|
|
(2)观察表,令m=l-a,n=l-b,探究m、n与s之间的关系,并对你的结论给予证明.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
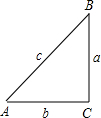 如图,在△ABC中,∠C=90°,角A、B、C的对边分别为a、b、c,设△ABC的面积为s,周长的一半为l.
如图,在△ABC中,∠C=90°,角A、B、C的对边分别为a、b、c,设△ABC的面积为s,周长的一半为l.
(1)填写表:
| 三边a、b、c | l-a | l-b | s |
| 3、4、5 | 3 | 2 | 6 |
| 5、12、13 | | | |
| 8、15、17 | | | |
(2)观察表,令m=l-a,n=l-b,探究m、n与s之间的关系,并对你的结论给予证明.
查看答案和解析>>


 在△ABC中,a,b,c分别为内角A,B,C所对的边,且满足
在△ABC中,a,b,c分别为内角A,B,C所对的边,且满足![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]()
![]() 大小;
大小;![]() 时,求
时,求![]() 的取值范围.
的取值范围.
![]() 是
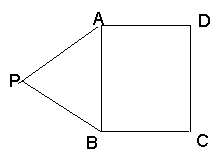
是![]() 的矩形,
的矩形,![]() 是正三角形,将
是正三角形,将![]() 沿
沿![]() 折起,使
折起,使![]() 如图2,
如图2,![]() 为
为![]() 的中点,设直线
的中点,设直线![]() 过点
过点![]() 且垂直于矩形
且垂直于矩形![]() 所在平面,点
所在平面,点![]() 是直线
是直线![]() 上的一个动点,且与点
上的一个动点,且与点![]() 位于平面
位于平面![]() 的同侧。
的同侧。![]() 平面
平面![]() ;
;![]() 的平面角为
的平面角为![]() ,若
,若![]() ,求线段
,求线段![]() 长的取值范围。
长的取值范围。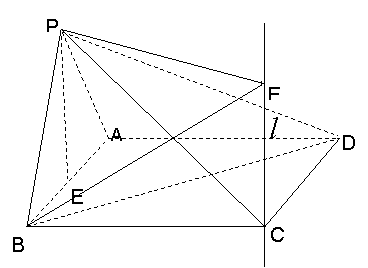
![]() 的左,右顶点,
的左,右顶点,![]() ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线![]() 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点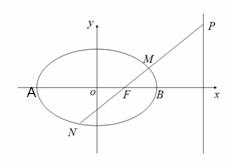 (2)求三角形MNT的面积的最大值
(2)求三角形MNT的面积的最大值![]()
![]() ,
,![]() 在
在![]() 上存在最大值与最小值,且其最大值与最小值的和为
上存在最大值与最小值,且其最大值与最小值的和为![]() ,试求
,试求![]() 和
和![]() 的值。
的值。![]() 为奇函数:
为奇函数:![]() ,使得
,使得![]() 在
在![]() 为增函数,
为增函数,![]() 为减函数,若存在,求出
为减函数,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;![]() 时,都有
时,都有![]() 恒成立,试求
恒成立,试求![]() 的取值范围.
的取值范围. 在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程ax2+bx-c=0为“△ABC的☆方程”.根据规定解答下列问题:
在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程ax2+bx-c=0为“△ABC的☆方程”.根据规定解答下列问题: 在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程ax2-bx-c=0为“△ABC的☆方程”.根据规定解答下列问题:
在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程ax2-bx-c=0为“△ABC的☆方程”.根据规定解答下列问题: 为“△ABC的☆方程”.根据规定解答下列问题:
为“△ABC的☆方程”.根据规定解答下列问题: 的根的情况是______(填序号):
的根的情况是______(填序号): 的解;
的解;
 是“△ABC的☆方程”
是“△ABC的☆方程”  的一个根,其中a,b,c均为整数,且
的一个根,其中a,b,c均为整数,且 ,求方程的另一个根.
,求方程的另一个根. 如图,在△ABC中,a,b,c分别为∠A,∠B,∠C的对边.
如图,在△ABC中,a,b,c分别为∠A,∠B,∠C的对边. 如图,在△ABC中,a,b,c分别为∠A,∠B,∠C的对边.
如图,在△ABC中,a,b,c分别为∠A,∠B,∠C的对边.

 如图,在△ABC中,∠BAC、∠B、∠C的对边分别为a、b、c,且(ab-1)2+(a-b)2=0.
如图,在△ABC中,∠BAC、∠B、∠C的对边分别为a、b、c,且(ab-1)2+(a-b)2=0. 如图,在△ABC中,∠C=90°,角A、B、C的对边分别为a、b、c,设△ABC的面积为s,周长的一半为l.
如图,在△ABC中,∠C=90°,角A、B、C的对边分别为a、b、c,设△ABC的面积为s,周长的一半为l. 如图,在△ABC中,∠C=90°,角A、B、C的对边分别为a、b、c,设△ABC的面积为s,周长的一半为l.
如图,在△ABC中,∠C=90°,角A、B、C的对边分别为a、b、c,设△ABC的面积为s,周长的一半为l.