
4. 用于比较大小
例6. 比较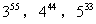 的大小。
的大小。
解: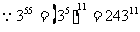

显然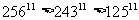
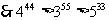
评注:例4中如果按有理数运算顺序计算是十分繁杂的,而逆用法则却极为方便;例5通过逆用法则,也简便获解;例3、例6直接求解,很难进行,但逆用幂的运算法则,问题就迎刃而解,足见适时逆用法则的巨大威力。
3. 用于求值
例5. 已知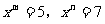 ,求
,求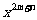 的值。
的值。
解:原式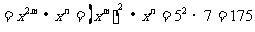
2. 用于计算
例4. 计算:
(1)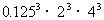 ;
;
(2)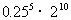
解:(1)原式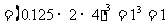
(2)原式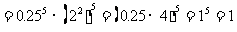
在规定的情况下,各个法则都是一个恒等式,运用时既可从左边到右边,也可以从右边到左边,虽应用范围有限,但灵活度大。
1. 用于确定个位数字
例3. 试确定 的个位数字
的个位数字
解:
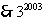 的个位数字是7
的个位数字是7
有理数的加减,打破了小学数学中的加与减的严格界限,把加、减统一成加法。这都是由于引进了负数,也正是由于引进了负数,小学时我们所熟悉的许多结论在有理数范围内都不一定成立了。下面的几个问题作为本文的结尾,请同学们认真思考并做出回答:
(1)“两个数相加,和一定大于或等于各个加数”吗?
(2)“两个数相减,差一定小于或等于被减数”吗?
(3)“一个数的3倍一定大于这个数的2倍”吗?
在初次进行有理数的加减运算时,首先要分清“+”、“-”号是运算符号还是性质符号。刚开始时,最好把性质符号用括号括起来,使性质符号与运算符号分开。如:正2加上负3,应写作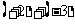 ,不能写成“
,不能写成“ ”。其次,要牢记运算的法则。第三,减法统一变加法。因为学了相反数后,减去一个数,等于加上这个数的相反数。这是有理数的减法法则,它把减法变成了加法。
”。其次,要牢记运算的法则。第三,减法统一变加法。因为学了相反数后,减去一个数,等于加上这个数的相反数。这是有理数的减法法则,它把减法变成了加法。
在小学数学中,“+”、“-”表示加号和减号。学习有理数后,“+”与“-”还表示正号与负号。
我们通常把四则运算中的加(+)、减(-)、乘(×)、除(÷)号叫运算符号;把表示正负数的正(+)、负(-)号叫性质符号。另外,负(-)号除了表示上述两种意义外,还表示一个数的相反数。如:-5可表示为5的相反数,而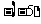 ,表示
,表示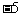 的相反数。
的相反数。
例6. 求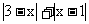 的最小值。
的最小值。
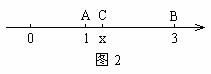
解:如图2,设数轴上的三点A、B、C所表示的数分别为1、3、x,其中C可视为一个动点,这样,此题就可转化为求 的最小值。由图形可知,当点C在线段AB上时
的最小值。由图形可知,当点C在线段AB上时 最小,此时
最小,此时 ,故当
,故当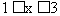 时,
时,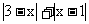 有最小值,其最小值为2。
有最小值,其最小值为2。
例5. 求代数式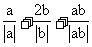 的值。
的值。
解:(1)当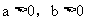 时,
时,
原式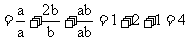
(2)当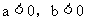 时,
时,
原式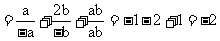
(3)当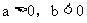 时,
时,
原式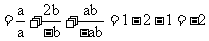
(4)当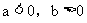 时,
时,
原式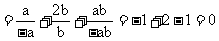
综上所述,所求代数式的值为4、 和0。
和0。
例4. 如果 ,那么a的取值范围是_________。
,那么a的取值范围是_________。
解:由已知式可知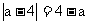
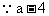 与
与 互为相反数
互为相反数

注意:在这里许多同学只重视 是一个负数,而忽视了
是一个负数,而忽视了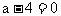 也成立这一特殊性,易把答案填为
也成立这一特殊性,易把答案填为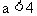 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com