
例6 如图,在 方格内已填好了两个数19和95,可以在其余的方格中填上适当的数,使每一行、每一列、以及每一条对角线上的三个数的和都相等,
方格内已填好了两个数19和95,可以在其余的方格中填上适当的数,使每一行、每一列、以及每一条对角线上的三个数的和都相等,
(1)求x;
(2)在题设的基础上,如果中间的空格上是100,请完成填图。

解:(1)设每一行、每一列、每一条对角线的三个数都相等的数是k


(2)中间填上100,从而不难求每行、每列、每条对角线的三个数的和为300,则其余空格上数字如图。

例5 对应实数x,y,设 ,等式右边是通常的加法和乘法,且
,等式右边是通常的加法和乘法,且
解:由题意,得
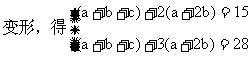
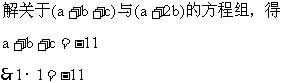
例1 对于任意实数m,等式
解:

例2 关于x的代数式 ,当x分别取1,2,-1时,y的值分别是4,7,10,求a,b,c的值。
,当x分别取1,2,-1时,y的值分别是4,7,10,求a,b,c的值。
解:根据题意,得

例3 已知 都是关于x,y的某个二元一次方程的解,求这个二元一次方程。
都是关于x,y的某个二元一次方程的解,求这个二元一次方程。
解:设这个二元一次方程为


例4 已知等式
解:由已知条件得

比较对应项的系数,得

3. 当 时,方程无解。
时,方程无解。
下面举例予以分析说明。
例1. 解关于x的方程
解:当 ,即
,即 时,方程有唯一解:
时,方程有唯一解:
当 ,即
,即 时,原方程可化为:
时,原方程可化为: ,方程无解
,方程无解
总结:此方程为什么不存在无穷解呢?因为只有当方程可化为 时,方程才能有无穷解,而当
时,方程才能有无穷解,而当 时,
时, ;
; 时,
时, ,a不可能既等于-2又等于3。所以不存在无穷解。
,a不可能既等于-2又等于3。所以不存在无穷解。
例2. 解关于x的方程
解:原方程可化为
当 ,即
,即 时,方程有唯一解:
时,方程有唯一解:
当 ,即
,即 时,方程有无数解
时,方程有无数解
总结:此方程没有无解的情况,因为方程可化为 ,而不会出现
,而不会出现 的情形。
的情形。
2. 当 时,方程有无数解;
时,方程有无数解;
1. 当 时,方程有唯一解;
时,方程有唯一解;
例5. (2001年江苏无锡中考题)
根据题意,完成下列填空:如图6所示, 与
与 是同一平面内的两条相交直线,它们有一个交点,如果在这个平面内,再画第3条直线
是同一平面内的两条相交直线,它们有一个交点,如果在这个平面内,再画第3条直线 ,那么这3条直线最多可有( )个交点;如果在这个平面内再画第4条直线
,那么这3条直线最多可有( )个交点;如果在这个平面内再画第4条直线 ,那么这4条直线最多可有( )个交点;由此我们可以猜想:在同一平面内,6条直线最多可有( )个交点。n(n为大于1的整数)条直线最多可有( )个交点(用含n的代数式表示)。
,那么这4条直线最多可有( )个交点;由此我们可以猜想:在同一平面内,6条直线最多可有( )个交点。n(n为大于1的整数)条直线最多可有( )个交点(用含n的代数式表示)。
解:(1)画图观察
 图6
图6
(2)列表归纳

(3)猜想:
 ,……
,……
于是,可猜想n条直线最多可有交点个数为:

于是,当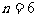 时,
时, 个交点。
个交点。
例4. 已知线段AB=8cm,在直线AB上画线段BC使它等于3cm,求线段AC的长。

图4
分析:由于点C可能在线段AB上,也可能在线段AB外,因此需要分类讨论。
解:当点C在线段AB上时,如图4所示, 。
。
当点C在线段AB外时,如图5所示, 。
。
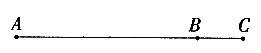
图5
因此线段AC长为5cm或11cm。
例3. 已知:如图3所示,C是线段AB上一点,点D、E分别是AC、CB的中点,若 ,求线段DE的长。
,求线段DE的长。

图3
解:∵D、E分别是AC、BC的中点

说明:解答本题的关键是逆用分配律得出待求线段和已知线段这个整体的关系。
例2. 点D、E在线段AB上,且都在AB中点的同侧,点D分AB为2:5两部分,点E分AB为4:5两部分,若DE=5cm,则AB的长为( )。

图2
解:由题意,得如图2所示,设AB=x,则 ,由
,由 ,得
,得 ,解得
,解得 ,即
,即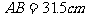 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com