例3. 甲、乙两人在环形跑道上练习跑步，已知环形跑道一圈长400米，乙每秒钟跑6米，甲的速度是乙的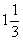倍。现在甲、乙两人在跑道上相距8米处同时出发，问经过多少秒钟后两人首次相遇？

　　 分析：虽然环行问题可转化为追及问题或相遇问题去解决，但本题既不明确甲、乙两人在环形跑道上是同向还是反向跑步，更不知同向跑步时谁在前谁在后，或反向跑步时两人之间的距离是哪一部分，所以解题时应分类讨论，逐一求解。

　　 解：设经过x秒甲、乙两人首次相遇。

　　 (1)若两人同向跑步，且甲在乙前面8米时，依题意，得方程：

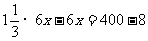
　　 解得：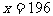

　 　(2)若两人同向跑步，且乙在甲前面8米时，依题意，得方程：

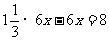
　　 解得：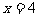

　　 (3)若两人反向跑步，且相距8米时，依题意，得方程：

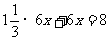
　　 解得：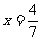

　　 (4)若两人反向跑步，且相距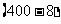米时，依题意，得方程：

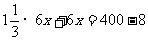
　　 解得：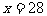

　　 答：当甲、乙两人在环形跑道上同向跑步时，经过196秒或4秒首次相遇，反向跑步时，经过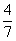或28秒首次相遇。

　 例2. 甲、乙两人分别从相距2.5千米的两地沿同一条公路同时同向出发进行骑自行车训练。已知甲、乙两人的速度分别为12.5千米/时和15千米/时，问经过几小时后两人相距3千米？

　　 分析：本题属行程问题中的追及问题，但不明确甲、乙两人谁在前，谁在后，因而要分两种情况求解。

　　 解：设经过x小时后两个相距3千米

　　 (1)当甲在乙前面时，依题意，可得方程

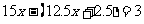
　　 解得：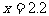

　　 (2)当乙在甲前面时，依题意，可得方程

　　 解得：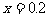

　　 答：经过2.2小时或0.2小时后两人相距3千米。

　 例1. A、B两站相距900千米，一列慢车从A站开出，速度为每小时55千米。同一时刻一列快车从B站开出，速度为每小时80千米，两车相向而行，经过多少小时两车相距45千米？

　　 分析：题中求“经过多少小时两车相距45千米？”但没有指出是相遇前两车相距45千米，还是相遇后两车相距45千米，因而情况不明，需分类求解。

　　 解：设经过x小时两车相距45千米

　　 (1)当相遇前两车相距45千米时，依题意，得：

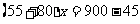
　　 解得：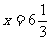

　　 (2)当相遇后两车又相距45千米时，依题意，得：

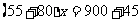
　　 解得：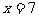

　　 答：经过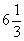小时或7小时两车相距45千米。

6. 已知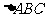：中，AB=AC，D是BC的中点，DE//AC，DF//AB，DE、DF分别交AB、AC于点E、F，求证：四边形AEDF是菱形。

5. 在平行四边形ABCD中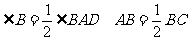，，M、N分别是AD、BC的中点。求证四边形ANCM是菱形。

4. 求证：过矩形各顶点平行于对角线的垂线围成的四边形是菱形。

3. 求证：顺次连结矩形四边中点所构成的四边形是菱形。

2. 求证：顺次连结等腰梯形上、下底的中点和两对角线的中点所构成的四边形是菱形。

1. 求证：顺次连结等腰梯形各边中点所构成的四边形是菱形。

4. 对角线互相垂直平分的四边形是菱形

　　 例4　 已知：如图4，中，BAC的平分线交BC于点D，E是AB上一点，且AE=AC，EF//BC交AD于点F。

　 　求证：四边形CDEF是菱形。

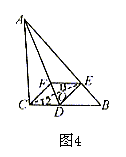
　　 证明：连结CE交AD于点O

　　 因为AC=AE

　　 所以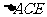为等腰三角形

　　 因为AO平分CAE

　　 所以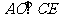，且OC=OE

　　 因为EF//CD，

　　 所以1=2

　　 所以OF=OD

　　 于是CE垂直平分DF

　　 所以四边形CDEF是菱形

　　 总结以上，得到下表

　　 练习：