
例1. 计算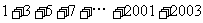 解:设
解:设
再把S倒过来写:
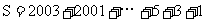
相加得: 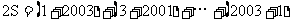
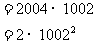
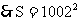
列代数式时,有时需将题中的字母代入公式,这就要求正确进行代换。如图,写出图中阴影部分面积的代数式为ab-(a-2x)(b-2x)。其中a与b分别表示长方形的长和宽,(a-2x)与(b-2x)分别表示小空白长方形的长和宽。▲
列代数时要按要求规范地书写。像数字与字母、字母与字母相乘可省略乘号不写,数与数相乘必须写乘号;除法可写成分数形式,带 分数与字母相乘需把代分数化为假分数,书写单位名称什么时不加括号,什么时要加括号。注意代数式括号的适当运用。
列代数式时,一般应在语言叙述的数量关系中,先读的先写,如a的2倍与b的3倍的差,为2a-3b,不同级运算的语言,且又要体现出先低级运算,要把代数式中代表低级运算的这部分括起来,如a与b的差的3倍,为3(a-b)。
要正确列代数式,只有分清数量之间的关系。如比m大3的数应为m+3;比一个数大3的数是m,则这个数为m-3;一个数是a的3位,这个数为3a;a是这个数的3倍,这个数为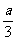 。不要见多就加,见小就减,见倍就乘。
。不要见多就加,见小就减,见倍就乘。
列代数式时,要先认真审题,抓住关键词语,仔细辩析词义。如“除”与“除以”,“平方的差(或平方差)”与“差的平方”的词义区分。例:“3除a”,“被3除得a”,“a与b两数的平方差”,“a与b两数差的平方”,分别为“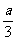 ”、“ 3a”、a2-b2、(a-b)2。
”、“ 3a”、a2-b2、(a-b)2。
例13. 已知抛物线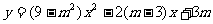 的顶点D在双曲线
的顶点D在双曲线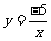 上,直线
上,直线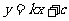 经过点D和点C(a、b)且使y随x的增大而减小,a、b满足方程组
经过点D和点C(a、b)且使y随x的增大而减小,a、b满足方程组 ,求这条直线的解析式。
,求这条直线的解析式。
解:由抛物线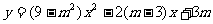 的顶点D(
的顶点D(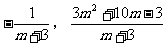 )在双曲线上,可求得抛物线的解析式为:
)在双曲线上,可求得抛物线的解析式为:
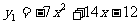 ,顶点D1(1,-5)及
,顶点D1(1,-5)及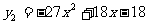
顶点D2(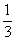 ,-15)
,-15)
解方程组得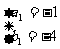 ,
,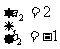
即C1(-1,-4),C2(2,-1)
由题意知C点就是C1(-1,-4),所以过C1、D1的直线是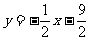 ;过C1、D2的直线是
;过C1、D2的直线是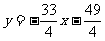
例12. 若方程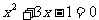 的两根分别为
的两根分别为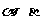 ,求经过点P(
,求经过点P(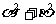 ,
,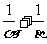 )和Q(
)和Q(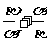 ,
,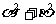 )的一次函数图像的解析式
)的一次函数图像的解析式
解:由根与系数的关系得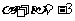 ,
,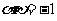
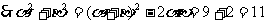 ,
,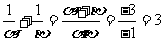
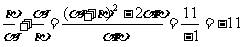
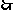 点P(11,3)、Q(-11,11)
点P(11,3)、Q(-11,11)
设过点P、Q的一次函数的解析式为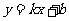
则有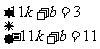
解得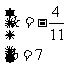
故这个一次函数的解析式为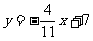
例11. 如图,在平面直角坐标系中,A、B是x轴上的两点,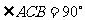 ,
,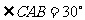 ,以AO、BO为直径的半圆分别交AC、BC于E、F两点,若C点的坐标为(0,3)。(1)求图像过A、B、C三点的二次函数的解析式,并求其对称轴;(2)求图像过点E、F的一次函数的解析式。
,以AO、BO为直径的半圆分别交AC、BC于E、F两点,若C点的坐标为(0,3)。(1)求图像过A、B、C三点的二次函数的解析式,并求其对称轴;(2)求图像过点E、F的一次函数的解析式。
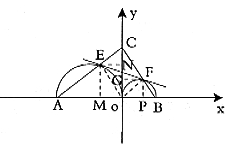
解:(1)由直角三角形的知识易得点A(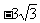 ,0)、B(
,0)、B(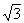 ,0),由待定系数法可求得二次函数解析式为
,0),由待定系数法可求得二次函数解析式为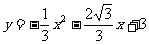 ,对称轴是
,对称轴是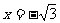
(2)连结OE、OF,则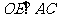 、
、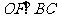 。过E、F分别作x、y轴的垂线,垂足为M、N、P、G,易求得E(
。过E、F分别作x、y轴的垂线,垂足为M、N、P、G,易求得E(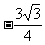 ,
,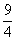 )、F(
)、F(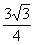 ,
,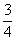 )由待定系数法可求得一次函数解析式为
)由待定系数法可求得一次函数解析式为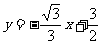
例10. 已知函数的图像过点A(1,4),B(2,2)两点,请写出满足上述条件的两个不同的函数解析式,并简要说明解答过程。
解:(1)若经过A、B两点的函数图像是直线,由两点式易得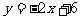
(2)由于A、B两点的横、纵坐标的积都等于4,所以经过A、B两点的函数图像还可以是双曲线,解析式为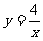
(3)其它(略)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com