
22.(本小题满分14分)
已知直线L过抛物线x2=2py(p>0)的焦点F,且与抛物线交于A,B两点,Q是线段AB的中点,M是抛物线的准线与y轴的交点,0是坐标原点
(1) 若直线L与x轴平行,且直线与抛物线所围区域的面积为6,求p的值.
(2)
过A,B两点分别作该抛物线的切线,两切线相交于N点,求证: ,
,
(3)
若p是不为1的正整数,当 ,△ABN的面积的取值范围为
,△ABN的面积的取值范围为 时,求:该抛物线的方程.
时,求:该抛物线的方程.
21.解:(1)当a=1时, ,其定义域是
,其定义域是 ,
,
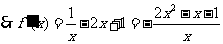 ---------------------------------1分
---------------------------------1分
令 ,即
,即 ,解得
,解得 或
或 .
.
∵x>0, 舍去.
舍去.
当 时,
时, ;当
;当 时,
时,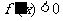 .
.
∴函数 在区间(0,1)上单调递增,在区间(1,+∞)上单调递减 ----------4分
在区间(0,1)上单调递增,在区间(1,+∞)上单调递减 ----------4分
∴当x=1时,函数 取得最大值,其值为
取得最大值,其值为 .
.
当 时,
时, ,即
,即 .
.
∴函数 只有一个零点. ---------------------6分
只有一个零点. ---------------------6分
(2)因为 其定义域为
其定义域为 ,
,
所以 -----------------------7分
-----------------------7分
①当a=0时, 在区间
在区间 上为增函数,不合题意----------8分
上为增函数,不合题意----------8分
②当a>0时, 等价于
等价于 ,即
,即 .
.
此时 的单调递减区间为
的单调递减区间为 .
.
依题意,得 解之得
解之得 ---------------------------------10分
---------------------------------10分
③当a<0时, 等价于
等价于 ,即
,即 ·
·
此时 的单调递减区间为
的单调递减区间为 ,
, 得
得
综上,实数a的取值范围是 ---------------------------------12分
---------------------------------12分
21.(12分)(本小题满分12分)‘
已知函数 .
.
(1)当a=1时,证明函数 只有一个零点;
只有一个零点;
(2)若函数 在区间(1,+∞)上是减函数,求实数a的取值范围.
在区间(1,+∞)上是减函数,求实数a的取值范围.
20.(本小题满分12)
定义 的“倒平均数”为
的“倒平均数”为 (
( )已知数列
)已知数列 的前n项的“倒平均数”为
的前n项的“倒平均数”为
(1)
求:数列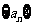 的通项公式
的通项公式
(2)
设函数 ,数列
,数列 满足
满足  、
、
记 ,求数列
,求数列 的前n项的和
的前n项的和
(3)
是否存在实数 ,使得当x≤
,使得当x≤ 时,
时, 对任意
对任意 恒成立?若存在,求出最大的实数
恒成立?若存在,求出最大的实数 ,若不存在,说明理由.
,若不存在,说明理由.
18解:(1)由 得:
得: =
=
则 +4(n-1),两式相减得
+4(n-1),两式相减得 (n≥2)
(n≥2)
又 =6适合上式,所以
=6适合上式,所以 ,(n∈N*)
4分
,(n∈N*)
4分
(2) 


两式相减得:
 8分
8分
(3)假设存在实数 ,使得当
,使得当 时,
时, ≤0对任意
≤0对任意 恒成立,则
恒成立,则 对任意
对任意 都成立,而
都成立,而 为单调增的
为单调增的 的最小值为
的最小值为 =3,令
=3,令 得:x≥3或x≤1 故存在最大的实数
得:x≥3或x≤1 故存在最大的实数 符合题意
12分
符合题意
12分
19.(本小题满分12分)
一个多面体的三视图和直观图如图所示,其中D为A A1的中点。
(1)求平面B1DC把多面体ABC-A1B1C1分成两部分的体积之比。
(2)在线段B1C上是否存在一点E,使A1E//平面BDC,若存在指出E点的位置,若不存在,说明理由。
(3)求直线BD与平面B1DC夹角的正弦值。


19 解:(1)由三视图可知直观图为直三棱柱且底面ABC中,BC⊥AC,BC=CC1=2,AC=1,
 ,
,
所以两部分体积之比为1:1 4分
(2)取B1C的中点E,BC中点F,连EF,A1E,DF,易证A1DFE为平行四边形,所以A1E∥DF,而DF 面BDC,A1E
面BDC,A1E 面BDC,所以A1E∥面BDC
面BDC,所以A1E∥面BDC
即存在E点,当E为B1C中点时有A1E∥面BDC 8分
(3)连C1D,易知CD⊥C1D,又CD⊥B1C1,所以CD⊥面B1C1D
所以面B1DC⊥面B1C1D,作C1M⊥B1D,则C1M⊥面B1DC
可求C1M= ,即B点到面B1DC的距离为
,即B点到面B1DC的距离为 ,又BD=
,又BD=
所以BD与面B1DC夹角的正弦值= 12分
12分
18. 解:(1)由题意得 ,
,

 列表略
列表略
因此
(2)第二小组第 次试验成功,前面
次试验成功,前面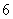 次试验中有
次试验中有 次失败,因此所求概率
次失败,因此所求概率

18. 已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为 ,某植物研究所分
,某植物研究所分 个小组分别独立开展该种子的发芽试验,每次实验种一粒种子,如果某次没有发芽,则称该次实验是失败的。
个小组分别独立开展该种子的发芽试验,每次实验种一粒种子,如果某次没有发芽,则称该次实验是失败的。
(1)第一小组做了 次实验,记该小组试验成功的次数为
次实验,记该小组试验成功的次数为 ,求
,求 的概率分布列及数学期望;
的概率分布列及数学期望;
(2)第二小组进行实验,到成功了 次为止,求在第
次为止,求在第 次成功之前共
次成功之前共 有次失败的概率。
有次失败的概率。
17.解:(Ⅰ)∵ ∴
∴ ----①,
----①, ----②
----②
由①得 ------③
------③
在△ABC中,由正弦定理得

∵  ∴
∴ ∴
∴ ,∵
,∵ ∴
∴ …………6分
…………6分
(Ⅱ) ∵ ,由余弦定理得
,由余弦定理得

 ,--④
,--④
由②得 -⑤ 由④⑤得
-⑤ 由④⑤得 ,∴
,∴ =
= . ……………………………12分
. ……………………………12分
17.(本小题满分12分)
已知:复数 ,
, ,且
,且 ,其中
,其中 、
、 为△ABC的内角,
为△ABC的内角, 、
、 、
、 为角
为角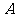 、
、 、
、 所对的边.
所对的边.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ) 若 ,求△ABC的面积.
,求△ABC的面积.
16. 给出下列四个命题:
(1)存在x∈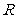 ,使不等式
,使不等式 成立
成立
(2)“p且q”为假是“p或q”为真的充分不必要条件
(3)“全等三角形的面积相等”的否命题
(4)对于线性相关的两个变量而言,若相关系数的绝对值越接近于1,则两个变量的相关程度就越大。
其中正确命题序号为 (4)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com