
例1.100件产品中,有98件合格品,2件次品 从这100件产品中任意抽出3件.
从这100件产品中任意抽出3件.
(1)一共有多少种不同的抽法;
(2)抽出的3件都不是次品的抽法有多少种?
(3)抽出的3件中恰好有1件是次品的抽法有多少种?
(4)抽出的3件中至少有1件是次品的取法有多少种?
解:(1) ;(2)
;(2) ;(3)
;(3) ;
;
(4)解法一:(直接法)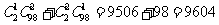 ;
;
解法二:(间接法) .
.
例2.从编号为1,2,3,…,10,11的共11个球中,取出5个球,使得这5个球的编号之和为奇数,则一共有多少种不同的取法?
解:分为三类:1奇4偶有 ; 3奇2偶有
; 3奇2偶有 ; 5奇1偶有
; 5奇1偶有 ,
,
∴一共有 +
+ +
+ .
.
例3.现有8名青年,其中有5名能胜任英语翻译工作;有4名青年能胜任德语翻译工作(其中有1名青年两项工作都能胜任),现在要从中挑选5名青年承担一项任务,其 中3名从事英语翻译工作,2名从事德语翻译工作,则有多少种不同的选法?
解:我们可以分为三类:
①让两项工作都能担任的青年从事英语翻译工作,有 ;
;
②让两项工作都能担任的青年从事德语翻译工作,有 ;
;
③让两项工作都能担任的青年不从事任何工作,有 ,
,
∴一共有 +
+ +
+ =42种方法.
=42种方法.
例4.甲、乙、丙三人值周,从周一至周六,每人值两天,但甲不值周一,乙不值周六,问可以排出多少种不同的值周表 ?
解法一:(排除法) .
.
解法二:分为两类:一类为甲不值周一,也不值周六,有 ;
;
另一类为甲不值周一,但值周六,有 ,
,
∴一共有 +
+ =42种方法.
=42种方法.
例5.6本不同的书全部送给5人,每人至少1本,有多少种不同的送书方法?
解:第一步:从6本不同的书中任取2本“捆绑”在一起看成一个元素有 种方法;
种方法;
第二步:将5个“不同元素(书)”分给5个人有 种方法.
种方法.
根据分步计数原理,一共有
 =1800种方法
=1800种方法 
12.组合数的性质2: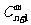 =
=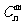 +
+

10.组合数公式:
或



11 组合数的性质1:
组合数的性质1: .规定:
.规定: ;
;
9.组合数的概念:从 个不同元素中取出
个不同元素中取出
 个元素的所有组合的个数,叫做从
个元素的所有组合的个数,叫做从 个不同元素中取出
个不同元素中取出 个元素的组合数.用符号
个元素的组合数.用符号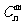 表示.
表示.
7.排列数的另一个计算公式: =
=


8 组合的概念:一般地,从
组合的概念:一般地,从 个不同元素中取出
个不同元素中取出
 个元素并成一组,叫做从
个元素并成一组,叫做从 个不同元素中取出
个不同元素中取出 个元素的一个组合
个元素的一个组合
说明:⑴不同元素;⑵“只取不排”--无序性;⑶相同组合:元素相同
5.排列数公式: (
( )
)
6 阶乘:
阶乘: 表示正整数1到
表示正整数1到 的连乘积,叫做
的连乘积,叫做 的阶乘
的阶乘 规定
规定 .
.
4.排列数的定义:从 个不同元素中,任取
个不同元素中,任取 (
( )个元素的所有排列的个数叫做从
)个元素的所有排列的个数叫做从 个元素中取出
个元素中取出 元素的排列数,用符号
元素的排列数,用符号 表示
表示
3.排列的概念:从 个不同元素中,任取
个不同元素中,任取 (
( )个元素(这里的被取元素各不相同)按照一定的顺序排成一列,叫做从
)个元素(这里的被取元素各不相同)按照一定的顺序排成一列,叫做从 个不同元素中取出
个不同元素中取出 个元素的一个排列
个元素的一个排列
1 分类计数原理:做一件事情,完成它可以有n类办法,在第一类办法中有
分类计数原理:做一件事情,完成它可以有n类办法,在第一类办法中有 种不同的方法,在第二类办法中有
种不同的方法,在第二类办法中有 种不同的方法,……,在第n类办法中有
种不同的方法,……,在第n类办法中有 种不同的方法
种不同的方法 那么完成这件事共有
那么完成这件事共有  种不同的方法
种不同的方法
2.分步计数原理:做一件事情,完成它需要分成n个步骤,做第一步有 种不同的方法,做第二步有
种不同的方法,做第二步有 种不同的方法,……,做第n步有
种不同的方法,……,做第n步有 种不同的方法,那么完成这件事有
种不同的方法,那么完成这件事有 种不同的方法
种不同的方法 
11.2009年以来,全国各地各部门加大文化建设投入力度,加快构建覆盖城乡的公共文化服务体 系,
系, 推
推 进公共文化设施免费开放,积极实施广播电视“村村通”、乡镇和社区综合文化站建设、
进公共文化设施免费开放,积极实施广播电视“村村通”、乡镇和社区综合文化站建设、
 农村电影放映,农家
农村电影放映,农家 书屋等重点文化工程,先进
书屋等重点文化工程,先进 文化的广泛传播,满足
文化的广泛传播,满足 了人民群众的精神文化生活,推动了经济、
了人民群众的精神文化生活,推动了经济、 社会的进步。
社会的进步。
节运用文化生活知识,说明文化在推动社会进步中有何作用?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com