
复习两角和与差的正弦、余弦、正切公式:


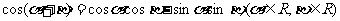



20. (本题满分16分)设函数 .
.
(1) 若曲线 在点
在点 处与直线
处与直线 相切, 求
相切, 求 的值;
的值;
(2) 求函数 的单调区间与极值点.
的单调区间与极值点.
19. (本题满分16分)在 中, 点
中, 点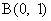 , 直线
, 直线 是角
是角 的平分线.直线
的平分线.直线
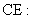
 是
是 边的中线.
边的中线.
(1) 求边 的直线方程;
的直线方程;
(2) 圆
 (
( ), 自点
), 自点 向圆
向圆 引切线
引切线 ,
, , 切点为
, 切点为 、
、 .
.
求:  的取值范围.
的取值范围.
18. (本题满分16分)某集团为了获得更大的收益, 每年要投入一定的资金用于广告促销. 经
调查投入广告费 (百万元), 可增加销售额约为
(百万元), 可增加销售额约为 (百万元)
(百万元) .
.
(1) 若该公司将当年的广告费控制在3百万元之内, 则应投入多少广告费, 才能使该公司由此
获得的收益最大?
(2) 现该公司准备共投入3百万元, 分别用于广告促销和技术改造. 经预测, 每投入技术改造
费 (百万元), 可增加的销售额约为
(百万元), 可增加的销售额约为 (百万元). 请设计一个资金分配方案, 使
(百万元). 请设计一个资金分配方案, 使
该公司由此获得的收益最大?(注: 收益=销售额-投放).
17.(本题满分14分)等比数列 的前
的前 项和为
项和为 , 已知
, 已知 成等差数列
成等差数列
(1)
求 的公比q; (2) 求
的公比q; (2) 求 , 求
, 求 .
. 

16. (本题满分14分)如图, 在四棱锥 中,
中,  是矩形,
是矩形,  平面
平面 ,
, 
 点
点 是
是 的中点, 点
的中点, 点 在
在 上移动.
上移动.
(1) 求三棱锥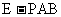 体积;
体积;
(2) 当点 为
为 的中点时, 试判断
的中点时, 试判断 与平面
与平面 的关系, 并说明理由;
的关系, 并说明理由;
 (3) 求证:
(3) 求证: 
15. (本题满分14分)在 中,
中, 分别是角A、B、C所对的边, 周长为
分别是角A、B、C所对的边, 周长为 ,
,
已知:  ,
,  , 且
, 且 ,
,
(1) 求边 的长; (2) 求角
的长; (2) 求角 的最大值.
的最大值.
14. 设函数
 数列
数列 满足:
满足:
 , 则数列
, 则数列 的前
的前 项和
项和 _ .
_ .
13. 已知 ,且
,且 , 若
, 若 恒成立, 则实数
恒成立, 则实数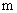 的取值范围是
的取值范围是
.
12. 对于任意实数x,
符号 表示x的整数部分, 即
表示x的整数部分, 即 是不超过x的最大整数”. 在实数轴
是不超过x的最大整数”. 在实数轴
R (箭头向右)上 是在点x左侧的第一个整数点, 当x是整数时
是在点x左侧的第一个整数点, 当x是整数时 就是x.这个函数
就是x.这个函数 叫做“
叫做“
取整函数”,
它在数学本身和生产实践中有广泛的应用. 那么, 
 _________________.
_________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com