3．在古罗马的一个广场上，一名理发师为一名奴隶刮胡子。另外两个人在附近玩球，其中一个人不小心用球砸到了理发师．导致他割了奴隶的喉咙。依据罗马法，在公共场所刮胡子是愚蠢的，因此奴隶本人对该事件负责。这表明罗马法　　　 　　　　　　　　　　　　　　　　 (　　 )

　　　 A．本质是维护私有制和贵族利益　　 　　 B．保障平民权益，实现社会公平

　　　 C．有利于调解矛盾，规范行为　　　 　　 D．是古代世界最完备的法律

2．著名学者钱穆认为，唐代“在三省体制下，决策不再是单纯的皇帝个人行为，皇帝的最后决定权包含在政务运行的程式中”。钱穆先生的观点是　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．唐朝专制皇权进一步加强　　　　　　　　

　　　 B．唐朝三省相互牵制

　　　 C．唐朝皇帝还未拥有足够的专制权力　　　　

　　　 D．唐朝实行集体决策机制

1．从地方行政组织来看，吕思勉先生把古代中国划分为“部落时代”、“封建时代”、“郡县时代”这三个先后相继的时代。其中与“封建时代”相对应的朝代是　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．西周　 　　　　　　　 B．秦朝　　 　　　　　　 C．西汉　　　　　 D．宋代

1若270°＜α＜360°，则等于 (　 D　 )

Asin　　 　　Bcos　　 C－sin　　　 D－cos

解：∵cos2α＝2cos²α－1　 ∴cosα＝2cos²－1

∴

又∵270°＜α＜360°　　 135°＜＜180°

∴原式＝

2求sin10°sin30°sin50°sin70°的值

解：∵sin10°＝cos80° ,sin50°＝cos40°, sin70°＝cos20°

∴原式＝cos80°cos40°cos20°

＝×

3求证：8cos⁴θ＝cos4θ+4cos2θ+3

证明：8cos⁴θ＝8(cos²θ)²＝8()²

＝2(cos²2θ+2cos2θ+1)＝2()+4cos2θ+2

＝cos4θ+4cos2θ+3

要理解并掌握二倍角公式以及推导，能正确运用二倍角的正弦、余弦、正切公式进行简单三角函数式的化简、求值与恒等式证明

二倍角公式是由和角公式由一般化归为特殊而来的，要注重这种基本数学思想方法，学会怎样去发现数学规律

4．

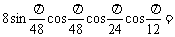
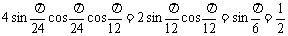
3．

(公式巩固性练习)求值：

1．sin22°30’cos22°30’=　 2．

例1 　不查表．求下列各式的值

　　　 (1)；　　　　　 (2)；

　　　 (3)；　　　　　　 (4)．

解: (1)=；　　　　　

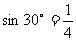(2)＝；

　 (3)＝；　　　　　　

(4)＝．

　例2不查表．求下列各式的值

(1)　 (2)

(3)　　　　　　　　 (4)

解: (1)

(2)

(3)

(4)

例3若tan q = 3，求sin2q - cos2q 的值

　解：sin2q - cos2q = 　　　　　　

例4 已知，求sin2a，cos2a，tan2a的值

　 解：∵　　 ∴

　　　 ∴sin2a = 2sinacosa =

　　　 cos2a = 　　　tan2a =

　二倍角公式的推导

　　 在公式，，中，当时，得到相应的一组公式：

　　 　　；

　　　　 ；

　　　　 ；

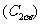
　　 因为，所以公式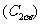可以变形为

　　　　 或　

公式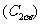，，，统称为二倍角的三角函数公式，简称为二倍角公式．

　　 　探究：(1)二倍角公式的作用在于用单角的三角函数来表达二倍角的三角函数，它适用于二倍角与单角的三角函数之间的互化问题．

　　 (2)二倍角公式为仅限于是的二倍的形式，其它如是的两倍，是的两倍，是的两倍，是的两倍等，所有这些都可以应用二倍角公式．因此，要理解“二倍角”的含义，即当时，就是的二倍角．凡是符合二倍角关系的就可以应用二倍角公式．尤其是“倍角”的意义是相对的

　　 (3)二倍角公式是从两角和的三角函数公式中，取两角相等时推导出，记忆时可联想相应角的公式．

　 　(4) 公式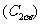，，，成立的条件是:　　 公式成立的条件是．其他

(5)熟悉“倍角”与“二次”的关系(升角-降次，降角-升次)

(6)特别注意公式的三角表达形式，且要善于变形：

　　这两个形式今后常用