2.(2009·徐州模拟)函数f(x)=sinx-cosx (x∈［-，0］)的单调递增区间是　　　　　 .

答案　

1.已知函数y=tanx在内是减函数,则的范围是　　　　　　 .

答案　 -1≤＜0

12.设、是方程x²-ax+b=0的两个根，试分析a＞2且b＞1是两根、均大于1的什么条件？　

解 　令p:a＞2,且b＞1;q: ＞1,且＞1,易知+=a, =b.　

①若a＞2,且b＞1,即不能推出＞1且＞1.　

可举反例：若所以由p推不出q　

②若＞1,且＞1，则+＞1+1=2, ＞1.所以由q可推出p.综合知p是q的必要不充分条件，也即a＞2,且b＞1是两根、均大于1的必要不充分条件.

11. a,b,c为实数，且a=b+c+1.证明：两个一元二次方程x²+x+b=0,x²+ax+c=0中至少有一个方程有两个不相等的实数根.

证明 　假设两个方程都没有两个不等的实数根，则　

?Δ₁=1-4b≤0,Δ₂=a²-4c≤0,　∴Δ₁+Δ₂=1-4b+a²-4c≤0.　

∵a=b+c+1,∴b+c=a-1.　∴1-4(a-1)+a²≤0,　

即a²-4a+5≤0.　但是a²-4a+5=(a-2)²+1＞0,故矛盾.　

所以假设不成立，原命题正确，即两个方程中至少有一个方程有两个不相等的实数根.

10. 已知x,y∈R.　

求证：|x+y|=|x|+|y|成立的充要条件是xy≥0.　

证明(充分性)　

若xy≥0,则x,y至少有一个为0或同号.∴|x+y|=|x|+|y|一定成立.　

(必要性)　若|x+y|=|x|+|y|,则(x+y)²=(|x|+|y|)²,　x²+2xy+y²=x²+2|xy|+y²,　

∴xy=|xy|,∴xy≥0.　综上，命题得证.

9. 求关于x的方程x²-mx+3m-2=0的两根均大于1的充要条件.　

解 　设方程的两根分别为x₁、x₂，则原方程有两个大于1的根的充要条件是　

　即

又∵x₁+x₂=m,x₁x₂=3m-2,　∴故所求的充要条件为m≥6+2.

8.设A=B则使AB成立的实数m的取值范围是　　　 .

答案 　m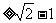

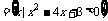7.设集合A=B则集合=　　　　　 .

答案　

6.(2008·安徽理，7)a＜0方程ax²+2x+1=0至少有一个负数根的　　　　 条件.

　 　　答案　 充分不必要

5.在△ABC中，“sin2A=”是“A=30°”的　　　　 条件.

　答案 　必要不充分性