
 随机变量:如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量随机变量常用希腊字母
随机变量:如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量随机变量常用希腊字母 、
、 等表示
等表示
 离散型随机变量:对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量
离散型随机变量:对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量
若 是随机变量,
是随机变量, ,其中
,其中 、
、 是常数,则
是常数,则 也是随机变量
也是随机变量
 连续型随机变量: 对于随机变量可能取的值,可以取某一区间内的一切值,这样的变量就叫做连续型随机变量
连续型随机变量: 对于随机变量可能取的值,可以取某一区间内的一切值,这样的变量就叫做连续型随机变量
 离散型随机变量与连续型随机变量的区别与联系: 离散型随机变量与连续型随机变量都是用变量表示随机试验的结果;但是离散型随机变量的结果可以按一定次序一一列出,而连续性随机变量的结果不可以一一列出
离散型随机变量与连续型随机变量的区别与联系: 离散型随机变量与连续型随机变量都是用变量表示随机试验的结果;但是离散型随机变量的结果可以按一定次序一一列出,而连续性随机变量的结果不可以一一列出
 离散型随机变量的分布列:设离散型随机变量
离散型随机变量的分布列:设离散型随机变量 可能取的值为
可能取的值为 、
、 、…、
、…、 、…
、…
 取每一个值
取每一个值
 的概率为
的概率为 ,则称表
,则称表
 |
 |
 |
… |
 |
… |
 |
 |
 |
… |
 |
… |
为随机变量 的概率分布,简称
的概率分布,简称 的分布列
的分布列
 离散型随机变量分布列的两个性质:任何随机事件发生的概率都满足:
离散型随机变量分布列的两个性质:任何随机事件发生的概率都满足: ≤
≤ ≤
≤ ,并且不可能事件的概率为
,并且不可能事件的概率为 ,必然事件的概率为
,必然事件的概率为 .由此你可以得出离散型随机变量的分布列都具有下面两个性质:
.由此你可以得出离散型随机变量的分布列都具有下面两个性质:
 ≥
≥ ,
, …;
…;
 …
…
对于离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率的和.即 ≥
≥
 离散型随机变量的二项分布:在一次随机试验中,某事件可能发生也可能不发生,在
离散型随机变量的二项分布:在一次随机试验中,某事件可能发生也可能不发生,在 次独立重复试验中这个事件发生的次数
次独立重复试验中这个事件发生的次数 是一个随机变量.如果在一次试验中某事件发生的概率是
是一个随机变量.如果在一次试验中某事件发生的概率是 ,那么在
,那么在 次独立重复试验中这个事件恰好发生
次独立重复试验中这个事件恰好发生 次的概率是
次的概率是
 ,(
,( …,
…,  )
)
于是得到随机变量 的概率分布如下:
的概率分布如下:
 |
 |
 |
… |
 |
… |
 |
 |
 |
 |
… |
 |
… |
 |
由于 恰好是二项展开式
恰好是二项展开式

中的各项的值,所以称这样的随机变量 服从二项分布,
服从二项分布,
记作 ,其中
,其中 ,
, 为参数,并记
为参数,并记 =
= .…
.…
 离散型随机变量的几何分布:在独立重复试验中,某事件第一次发生时,所作试验的次数
离散型随机变量的几何分布:在独立重复试验中,某事件第一次发生时,所作试验的次数 也是一个正整数的离散型随机变量.“
也是一个正整数的离散型随机变量.“ ”表示在第
”表示在第 次独立重复试验时事件第一次发生.如果把
次独立重复试验时事件第一次发生.如果把 次试验时事件
次试验时事件 发生记为
发生记为 、事件
、事件 不发生记为
不发生记为 ,
, ,
,  ,那么
,那么

 …,
…, 

于是得到随机变量 的概率分布如下:
的概率分布如下:
 |
 |
 |
 |
… |
 |
… |
 |
 |
 |
 |
… |
 |
… |
称这样的随机变量 服从几何分布,
服从几何分布,
记作
 ,其中
,其中 …,
…,
 求离散型随机变量分布列的步骤:
求离散型随机变量分布列的步骤: 要确定随机变量
要确定随机变量 的可能取值有哪些.明确取每个值所表示的意义;
的可能取值有哪些.明确取每个值所表示的意义; 分清概率类型,计算
分清概率类型,计算 取得每一个值时的概率(取球、抽取产品等问题还要注意是放回抽样还是不放回抽样;
取得每一个值时的概率(取球、抽取产品等问题还要注意是放回抽样还是不放回抽样; 列表对应,给出分布列,并用分布列的性质验证.
列表对应,给出分布列,并用分布列的性质验证.
 几种常见的分布列的求法:
几种常见的分布列的求法: 取球、投骰子、抽取产品等问题的概率分布,关键是概率的计算.所用方法主要有划归法、数形结合法、对应法等对于取球、抽取产品等问题,还要注意是放回抽样还是不放回抽样.
取球、投骰子、抽取产品等问题的概率分布,关键是概率的计算.所用方法主要有划归法、数形结合法、对应法等对于取球、抽取产品等问题,还要注意是放回抽样还是不放回抽样. 射击问题:若是一人连续射击,且限制在
射击问题:若是一人连续射击,且限制在 次射击中发生
次射击中发生 次,则往往与二项分布联系起来;若是首次命中所需射击的次数,则它服从几何分布,若是多人射击问题,一般利用相互独立事件同时发生的概率进行计算.
次,则往往与二项分布联系起来;若是首次命中所需射击的次数,则它服从几何分布,若是多人射击问题,一般利用相互独立事件同时发生的概率进行计算.
 对于有些问题,它的随机变量的选取与所问问题的关系不是很清楚,此时要仔细审题,明确题中的含义,恰当地选取随机变量,构造模型,进行求解.
对于有些问题,它的随机变量的选取与所问问题的关系不是很清楚,此时要仔细审题,明确题中的含义,恰当地选取随机变量,构造模型,进行求解.
 (
( 浙江文)甲、乙两人进行乒乓球比赛,比赛规则为“
浙江文)甲、乙两人进行乒乓球比赛,比赛规则为“ 局
局 胜”,即以先赢
胜”,即以先赢 局者为胜,根据经验,每局比赛中甲获胜的概率为
局者为胜,根据经验,每局比赛中甲获胜的概率为 ,则本次比赛甲获胜的概率是
,则本次比赛甲获胜的概率是 







 (
( 辽宁)甲、乙两人独立地解同一问题,甲解决这个问题的概率是
辽宁)甲、乙两人独立地解同一问题,甲解决这个问题的概率是 ,乙解决这个问题的概率是
,乙解决这个问题的概率是 ,那么恰好有
,那么恰好有 人解决这个问题的概率是
人解决这个问题的概率是








 (
( 湖北)某篮运动员在三分线投球的命中率是
湖北)某篮运动员在三分线投球的命中率是 ,他投球
,他投球 次,恰好投进
次,恰好投进 个球的概率
(用数值作答)
个球的概率
(用数值作答)
 (
( 湖北文)接种某疫苗后,出现发热反应的概率为
湖北文)接种某疫苗后,出现发热反应的概率为 ,现有
,现有 人接种了该疫苗,至少有
人接种了该疫苗,至少有 人出现发热反应的概率为 (精确到
人出现发热反应的概率为 (精确到 )
)
 (
( 湖南文)某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力,每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有
湖南文)某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力,每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有 ,参加过计算机培训的有
,参加过计算机培训的有 ,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
 任选
任选 名下岗人员,求该人参加过培训的概率;
名下岗人员,求该人参加过培训的概率;
 任选
任选 名下岗人员,求这
名下岗人员,求这 人中至少有
人中至少有 人参加过培养的概率.
人参加过培养的概率.
 (
( 重庆文)甲、乙、丙三人在同一办公室工作。办公室只有一部电话机,设经过该机打进的电话是打给甲、乙、丙的概率依次为
重庆文)甲、乙、丙三人在同一办公室工作。办公室只有一部电话机,设经过该机打进的电话是打给甲、乙、丙的概率依次为 、
、 、
、 .若在一段时间内打进三个电话,且各个电话相互独立.求:
.若在一段时间内打进三个电话,且各个电话相互独立.求: 这三个电话是打给同一个人的概率;
这三个电话是打给同一个人的概率; 这三个电话中恰有两个是打给甲的概率;
这三个电话中恰有两个是打给甲的概率;
问题1.( 陕西文)甲、乙、丙
陕西文)甲、乙、丙 人投篮,投进的概率分别是
人投篮,投进的概率分别是 ,
, ,
, .现
.现 人各投篮
人各投篮 次,求:
次,求:
 人都投进的概率;
人都投进的概率;
 人中恰有
人中恰有 人投进的概率.
人投进的概率.
问题2.( 北京文)甲、乙两人各进行
北京文)甲、乙两人各进行 次射击,甲每次击中目标的概率为
次射击,甲每次击中目标的概率为 ,乙每次击中目标的概率
,乙每次击中目标的概率 ,
,  甲恰好击中目标的
甲恰好击中目标的 次的概率;
次的概率;  乙至少击中目标
乙至少击中目标 次的概率;
次的概率; 求乙恰好比甲多击中目标
求乙恰好比甲多击中目标 次的概率.
次的概率.
问题3.( 重庆文)设甲、乙两人每次射击命中目标的概率分别为
重庆文)设甲、乙两人每次射击命中目标的概率分别为 和
和 ,且各次射击相互独立.
,且各次射击相互独立. 若甲、乙各射击一次,求甲命中但乙未命中目标的概率;
若甲、乙各射击一次,求甲命中但乙未命中目标的概率;
 若甲、乙各射击两次,求两人命中目标的次数相等的概率.
若甲、乙各射击两次,求两人命中目标的次数相等的概率.
 相互独立事件:事件
相互独立事件:事件 (或
(或 )是否发生对事件
)是否发生对事件 (或
(或 )发生的概率没有影响,这样的两个事件叫做相互独立事件.
)发生的概率没有影响,这样的两个事件叫做相互独立事件.
若 与
与 是相互独立事件,则
是相互独立事件,则 与
与 ,
, 与
与 ,
, 与
与 也相互独立.
也相互独立.
 互斥事件与相互独立事件是有区别的:
互斥事件与相互独立事件是有区别的:
两事件互斥是指同一次试验中两事件不能同时发生,两事件相互独立是指不同试验下,二者互不影响;两个相互独立事件不一定互斥,即可能同时发生,而互斥事件不可能同时发生.
 相互独立事件同时发生的概率:
相互独立事件同时发生的概率:
事件 相互独立,
相互独立,  .
.
 独立重复试验的定义:在同样条件下进行的各次之间相互独立的一种试验.
独立重复试验的定义:在同样条件下进行的各次之间相互独立的一种试验.
 关于相互独立事件也要抓住以下特征加以理解:
关于相互独立事件也要抓住以下特征加以理解:
第一,相互独立也是研究两个事件的关系;第二,所研究的两个事件是在两次试验中得到的;第三,两个事件相互独立是从“一个事件的发生对另一个事件的发生的概率没有影响”来确定的.
 独立重复试验的概率公式:如果在一次试验中某事件发生的概率是
独立重复试验的概率公式:如果在一次试验中某事件发生的概率是 ,那么在
,那么在 次独立重复试验中这个事恰好发生
次独立重复试验中这个事恰好发生 次的概率
次的概率
 表示事件
表示事件 在
在 次独立重复试验中恰好发生了
次独立重复试验中恰好发生了 次的概率
次的概率
 关于独立重复试验要从三个方面理解:
关于独立重复试验要从三个方面理解:
第一:每次实验都在同样条件下进行;第二:各次实验中的事件是相互独立的;第三:每次实验只有两种结果,即事件要么发生,要么不发生,它与实验的序号无关.
 (
( 重庆文)若
重庆文)若 把钥匙中只有
把钥匙中只有 把能打开某锁,则从中任取
把能打开某锁,则从中任取 把能将该锁打开的概率为
把能将该锁打开的概率为
 (
( 四川) 从
四川) 从 到
到 这
这 个数字中任取
个数字中任取 个数字组成一个没有重复数字的三位数,
个数字组成一个没有重复数字的三位数,
这个数不能被 整除的概率为
整除的概率为 







 (
( 浙江)甲、乙两袋装有大小相同的红球和白球,甲袋装有
浙江)甲、乙两袋装有大小相同的红球和白球,甲袋装有 个红球,
个红球, 个白球;乙袋装有
个白球;乙袋装有 个红球,
个红球, 个白球.两甲,乙两袋中各任取
个白球.两甲,乙两袋中各任取 个球.
个球.
 若
若 ,求取到的
,求取到的 个球全是红球的概率;
个球全是红球的概率;
 若取到的
若取到的 个球中至少有
个球中至少有 个红球的概率为
个红球的概率为 ,求
,求 .
.

 袋中有
袋中有 个编号为
个编号为 ,…,
,…, 的小球,从中任意随机取出
的小球,从中任意随机取出 个,求至少有
个,求至少有 个编号为奇数的概率;
个编号为奇数的概率; 同时掷
同时掷 枚骰子时,求出现的点数的和是
枚骰子时,求出现的点数的和是 的倍数的概率.
的倍数的概率.
问题1. 从装有
从装有 个红球和
个红球和 各白球的口袋中任取两个球,那么下列事件中互斥事件的个数是
各白球的口袋中任取两个球,那么下列事件中互斥事件的个数是 
 个
个 
 个
个 
 个
个 
 个
个
①至少有 个白球,都是白球;②至少有
个白球,都是白球;②至少有 个白球,至少有
个白球,至少有 个红球;
个红球;
③恰有 个白球,恰有
个白球,恰有 个白球;④至少有
个白球;④至少有 个白球,都是红球.
个白球,都是红球.
 将一枚骰子向上抛掷一次,设事件
将一枚骰子向上抛掷一次,设事件 表示向上的一面出现奇数点,事件
表示向上的一面出现奇数点,事件 表示向上的一面出现的点数不超过
表示向上的一面出现的点数不超过 ,事件
,事件 表示向上的一面出现的点数不少于
表示向上的一面出现的点数不少于 ,则
,则

 与
与 是互斥而非对立事件
是互斥而非对立事件 
 与
与 是对立事件
是对立事件

 与
与 互斥而非对立事件
互斥而非对立事件

 与
与
 与
与 是对立事件
是对立事件
问题2. 从分别写有
从分别写有 的六件卡片中,任取三张并组成三位数,计算:
的六件卡片中,任取三张并组成三位数,计算:
①这个三位数是偶数的概率;②这个三位数能被三整除的概率;③这个三位数比 小的概率.
小的概率.
 (
( 天津)已知甲盒内有大小相同的
天津)已知甲盒内有大小相同的 个红球和
个红球和 个黑球,乙盒内有大小相同的
个黑球,乙盒内有大小相同的 个红球和
个红球和 个黑球.现从甲、乙两个盒内各任取
个黑球.现从甲、乙两个盒内各任取 个球.
个球.
①略;②求取出的 个球中恰有
个球中恰有 个红球的概率;③略.
个红球的概率;③略.
 (
( 重庆)从
重庆)从 张
张 元,
元, 张
张 元,
元, 张
张 元的奥运预赛门票中任取
元的奥运预赛门票中任取 张,则所取
张,则所取 张中至少有
张中至少有 张价格相同的概率为
张价格相同的概率为








问题3.从男女生共有 人的班中,选出两名代表,每人当选的机会均等,如果选的同性代表的概率是
人的班中,选出两名代表,每人当选的机会均等,如果选的同性代表的概率是 ,求该班中男女相差几名?
,求该班中男女相差几名?
问题4.( 全国Ⅱ文)从某批产品中,有放回地抽取产品二次,每次随机抽取
全国Ⅱ文)从某批产品中,有放回地抽取产品二次,每次随机抽取 件,假设事件
件,假设事件 :“取出的
:“取出的 件产品中至多有
件产品中至多有 件是二等品”的概率
件是二等品”的概率 .
.
 求从该批产品中任取
求从该批产品中任取 件是二等品的概率
件是二等品的概率 ;
;
 若该批产品共
若该批产品共 件,从中任意抽取
件,从中任意抽取 件,求事件
件,求事件 :“取出的
:“取出的 件产品中至少有一件二等品”的概率
件产品中至少有一件二等品”的概率 .
.
 互斥事件的概念:不可能同时发生的个事件叫做互斥事件.
互斥事件的概念:不可能同时发生的个事件叫做互斥事件. 、
、 互斥,即事件
互斥,即事件 、
、 不可能同时发生,这时
不可能同时发生,这时 ,
,
一般地:如果事件 中的任何两个都是互斥的,那么就说事件
中的任何两个都是互斥的,那么就说事件 彼此互斥.
彼此互斥.
 对立事件的概念:事件
对立事件的概念:事件 和事件
和事件 必有一个发生的互斥事件
必有一个发生的互斥事件
 、
、 对立,即事件
对立,即事件 、
、 不可能同时发生,但
不可能同时发生,但 、
、 中必然有一个发生
中必然有一个发生 这时
这时 ,
,

 ,一般地,
,一般地, .
.
 对于互斥事件要抓住如下的特征进行理解:
对于互斥事件要抓住如下的特征进行理解:
第一,互斥事件研究的是两个事件之间的关系;第二,所研究的两个事件是在一次试验中涉及的;第三,两个事件互斥是从试验的结果不能同时出现来确定的.
从集合角度来看, 、
、 两个事件互斥,则表示
两个事件互斥,则表示 、
、 这两个事件所含结果组成的集合的交集是空集.
这两个事件所含结果组成的集合的交集是空集.
对立事件是互斥事件的一种特殊情况,是指在一次试验中有且仅有一个发生的两个事件,集合 的对立事件记作
的对立事件记作 ,从集合的角度来看,事件
,从集合的角度来看,事件 所含结果的集合正是全集
所含结果的集合正是全集 中由事件
中由事件 所含结果组成集合的补集,即
所含结果组成集合的补集,即 ,
, 。对立事件一定是互斥事件,但互斥事件不一定是对立事件.
。对立事件一定是互斥事件,但互斥事件不一定是对立事件.
当 和
和 互斥时,事件
互斥时,事件 的概率满足加法公式:
的概率满足加法公式:
 (
( 、
、 互斥)当计算事件
互斥)当计算事件 的概率
的概率 比较困难时,有时计算它的对立事件
比较困难时,有时计算它的对立事件 的概率则要容易些,为此有
的概率则要容易些,为此有 .
.
 互斥事件的概率的求法:如果事件
互斥事件的概率的求法:如果事件 彼此互斥,那么
彼此互斥,那么
 =
= .
.
 分类讨论思想:分类讨论思想是解决互斥事件有一个发生的概率的一个重要的指导思想.
分类讨论思想:分类讨论思想是解决互斥事件有一个发生的概率的一个重要的指导思想.
 (
( 福建)在一个口袋中装有
福建)在一个口袋中装有 个白球和
个白球和 个黑球,这些球除颜色外完全相同.从中摸出
个黑球,这些球除颜色外完全相同.从中摸出 个球,至少摸到
个球,至少摸到 个黑球的概率等于
个黑球的概率等于







 (
( 上海)两部不同的长篇小说各由第一、二、三、四卷组成,每卷
上海)两部不同的长篇小说各由第一、二、三、四卷组成,每卷 本,共
本,共 本.将它们任意地排成一排,左边
本.将它们任意地排成一排,左边 本恰好都属于同一部小说的概率是
(结果用分数表示).
本恰好都属于同一部小说的概率是
(结果用分数表示).
 (
( 重庆)某轻轨列车有
重庆)某轻轨列车有 节车厢,现有
节车厢,现有 位乘客准备乘坐,设每一位乘客进入每节车厢是等可能的,则这
位乘客准备乘坐,设每一位乘客进入每节车厢是等可能的,则这 位乘客进入各节车厢的人数恰好为
位乘客进入各节车厢的人数恰好为 的概率为
的概率为
 (
( 湖北)以平行六面体
湖北)以平行六面体 的任意三个顶点为顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面的概率
的任意三个顶点为顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面的概率 为
为








 (
( 江西文)栽培甲、乙两种果树,先要培育成苗,然后再进行移栽.已知甲、乙两种果树成苗的概率分别为
江西文)栽培甲、乙两种果树,先要培育成苗,然后再进行移栽.已知甲、乙两种果树成苗的概率分别为 ,
, ,移栽后成活的概率分别为
,移栽后成活的概率分别为 ,
, .
.
 求甲、乙两种果树至少有一种果树成苗的概率;
求甲、乙两种果树至少有一种果树成苗的概率;
 求恰好有一种果树能培育成苗且移栽成活的概率.
求恰好有一种果树能培育成苗且移栽成活的概率.
 (
( 北京文)某条公共汽车线路沿线共有
北京文)某条公共汽车线路沿线共有 个车站(包括起点站和终点站),在起点站开出的一辆公共汽车上有
个车站(包括起点站和终点站),在起点站开出的一辆公共汽车上有 位乘客,假设每位乘客在起点站之外的各个车站下车是等可能的.求:
位乘客,假设每位乘客在起点站之外的各个车站下车是等可能的.求:
 这
这 位乘客在其不相同的车站下车的概率;
位乘客在其不相同的车站下车的概率;
 这
这 位乘客中恰有
位乘客中恰有 人在终点站下车的概率;
人在终点站下车的概率;
 (
( 届高三成都名校联盟预测二)从单词“
届高三成都名校联盟预测二)从单词“ ”中选取
”中选取 个不同的字母排成
个不同的字母排成
一排,则含“ ”(“
”(“ ”相连且顺序不变)的概率为
”相连且顺序不变)的概率为








 从分别写有
从分别写有 的五张卡片里任取两张,这两张卡片里的字母恰好是按照字母顺序相邻排列的概率等于
的五张卡片里任取两张,这两张卡片里的字母恰好是按照字母顺序相邻排列的概率等于 







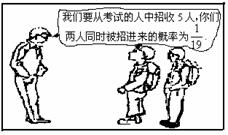
 两位同学去某大学参加自主招生考试,根据
两位同学去某大学参加自主招生考试,根据
右图学校负责人与他们两人的对话,可推断
出参加考试的人数为








湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com