
 若
若 ,则
,则 







 (
( 届高三昆明一中模拟)设函数
届高三昆明一中模拟)设函数
 ,若
,若
是偶函数,则 等于
等于 







 (
( 届高三江苏徐州模拟)设函数
届高三江苏徐州模拟)设函数
 是奇函数,
是奇函数,
则
 若
若 ,
, ,
, ,则
,则








 函数
函数 的单调递减区间是
的单调递减区间是
 ①函数
①函数 在它的定义域内是增函数;②若
在它的定义域内是增函数;②若 、
、 是第一象限角,且
是第一象限角,且 ,
,
则 ;③函数
;③函数 一定是奇函数;④函数
一定是奇函数;④函数 的
的
最小正周期为 .上列四个命题中,正确的命题是
.上列四个命题中,正确的命题是  ①
① ④
④ ①、②
①、② ②、③
②、③
 设定义域为
设定义域为 的奇函数
的奇函数 是减函数,若当
是减函数,若当 时,
时,
 ,求
,求 的值.
的值.
 试讨论函数:
试讨论函数: 的奇偶性。
的奇偶性。
 (
( 届湖南师大附中高三月考)已知函数
届湖南师大附中高三月考)已知函数 。
。
 若函数
若函数 的图象关于点
的图象关于点 对称,且
对称,且 ,求
,求 的值;
的值;
 设
设 :
: ,
, :
: ,若
,若 是
是 的充分条件,求实数
的充分条件,求实数 的取值范围。
的取值范围。
问题1. 判断下列函数的奇偶性:

 ;
;
 ;
;

 ;
;
 ;
;

问题2.比较下列各组中两个值的大小:

 ,
, ,
, ;
;
 ,
, .
.
问题3. 求下列函数的单调递增区间:①
求下列函数的单调递增区间:① ;
;
② ;③
;③ ;④
;④
 (
( 全国Ⅰ)函数
全国Ⅰ)函数 的一个单调增区间是
的一个单调增区间是








 (
( 福建)已知函数
福建)已知函数
 在区间
在区间 上的最小值是
上的最小值是 ,
,
则 的最小值等于
的最小值等于









 为奇函数
为奇函数 ;函数
;函数 为偶函数
为偶函数
 为偶函数
为偶函数 ;函数
;函数 为奇函数
为奇函数
 函数
函数
 的单调增区间可由
的单调增区间可由
解出,单调减区间可由 解出;
解出;
函数
 的单调增区间可由
的单调增区间可由
解出,单调减区间可由
 解出
解出
三角函数的奇偶性和单调性具体如下表:
|
函数 |
奇偶性 |
单调区间 |
 |
奇 |
在 上增 上增在  减 减 |
 |
偶 |
在 上增 上增在  减 减 |
 |
奇 |
在 上增 上增 |
 (
( 四川)函数
四川)函数 的最小正周期为
的最小正周期为 







 (
( 上海)函数
上海)函数 的最小正周期
的最小正周期
 (
( 福建)已知函数
福建)已知函数
 在区间
在区间 上的最小值是
上的最小值是 ,则
,则
的最小值等于 







 (
( 安徽文)解不等式
安徽文)解不等式 .
.
 (
( 天津)已知函数
天津)已知函数 ,
, .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)求函数 在区间
在区间 上的最小值和最大值.
上的最小值和最大值.
 (
( 重庆)设
重庆)设 .(Ⅰ)求
.(Ⅰ)求 的最大值及最小正周期;
的最大值及最小正周期;
(Ⅱ)若锐角 满足
满足 ,求
,求 的值.
的值.
 求函数
求函数 的定义域.
的定义域.
 函数
函数 的定义域为
的定义域为
 若方程
若方程 有解,则
有解,则
 (
( 江西)设函数
江西)设函数 ,则
,则 为
为
 周期函数,最小正周期为
周期函数,最小正周期为
 周期函数,最小正周期为
周期函数,最小正周期为
 周期函数,数小正周期为
周期函数,数小正周期为
 非周期函数
非周期函数
 (
( 全国Ⅱ)函数
全国Ⅱ)函数 的最小正周期是
的最小正周期是 





 2
2
 函数
函数 的最小正周期为
的最小正周期为
 函数
函数 的周期是
的周期是
 已知函数
已知函数 ,求
,求 的定义域,判断它的奇偶性,并求其值域
的定义域,判断它的奇偶性,并求其值域
问题1. 求下列函数的定义域:

 ;
;
 ;
;

问题2.求下列函数的值域:

 ;
;
 ;
;
 ;
;
 .
.
问题3.求下列函数的周期:

 ;
;
 ;
;

问题4.已知函数 的定义域为
的定义域为 ,值域为
,值域为 ,求常数
,求常数 的值.
的值.
 求三角函数的定义域实质就是解三角不等式(组).一般可用三角函数的图象或三角函数线确定三角不等式的解.列三角不等式,既要考虑分式的分母不能为零;偶次方根被开方数大于等于零;对数的真数大于零及底数大于零且不等于1,又要考虑三角函数本身的定义域;
求三角函数的定义域实质就是解三角不等式(组).一般可用三角函数的图象或三角函数线确定三角不等式的解.列三角不等式,既要考虑分式的分母不能为零;偶次方根被开方数大于等于零;对数的真数大于零及底数大于零且不等于1,又要考虑三角函数本身的定义域;
 求三角函数的值域的常用方法:①化为求代数函数的值域;②化为求
求三角函数的值域的常用方法:①化为求代数函数的值域;②化为求 的值域;③化为关于
的值域;③化为关于 (或
(或 )的二次函数式;
)的二次函数式;
 三角函数的周期问题一般将函数式化为
三角函数的周期问题一般将函数式化为 (其中
(其中 为三角函数,
为三角函数, ).
).
三角函数的定义域、值域及周期如下表:
|
函数 |
定义域 |
值域 |
周期 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 (
( 天津)要得到函数
天津)要得到函数 的图象,只需将函数
的图象,只需将函数 的
的
图象上所有的点的
 横坐标缩短到原来的
横坐标缩短到原来的 倍(纵坐标不变),再向左平行移动
倍(纵坐标不变),再向左平行移动 个单位长度
个单位长度
 横坐标缩短到原来的
横坐标缩短到原来的 倍(纵坐标不变),再向右平行移动
倍(纵坐标不变),再向右平行移动 个单位长度
个单位长度
 横坐标伸长到原来的
横坐标伸长到原来的 倍(纵坐标不变),再向左平行移动
倍(纵坐标不变),再向左平行移动 个单位长度
个单位长度
 横坐标伸长到原来的
横坐标伸长到原来的 倍(纵坐标不变),再向右平行移动
倍(纵坐标不变),再向右平行移动 个单位长度
个单位长度
 (
( 江苏)为了得到函数
江苏)为了得到函数 的图像,只需把函数
的图像,只需把函数 的图像上所有的点
的图像上所有的点
 向左平移
向左平移 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 倍(纵坐标不变)
倍(纵坐标不变)
 向右平移
向右平移 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 倍(纵坐标不变)
倍(纵坐标不变)
 向左平移
向左平移 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的 倍(纵坐标不变)
倍(纵坐标不变)
 向右平移
向右平移 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的 倍(纵坐标不变)
倍(纵坐标不变)
 (
( 安徽)函数
安徽)函数 的图象为
的图象为 ,
,
①图象 关于直线
关于直线 对称;②函数
对称;②函数 在区间
在区间 内是增函数;
内是增函数;
③由 的图象向右平移
的图象向右平移 个单位长度可以得到图象
个单位长度可以得到图象 .
.
以上三个论断中,正确论断的个数是 








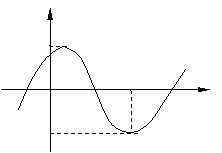 (
( 安徽)将函数
安徽)将函数 的图象按向量
的图象按向量
 平移,平移后的图象如图所示,
平移,平移后的图象如图所示,
则平移后的图象所对应函数的解析式是








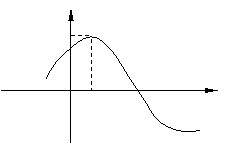
 (
( 福建)函数
福建)函数
 ,
,
 )的部分图象如图,则
)的部分图象如图,则








 (
( 福建)已知函数
福建)已知函数 的最小正周期为
的最小正周期为 ,则该函数的图象
,则该函数的图象 关于点
关于点 对称
对称  关于直线
关于直线 对称
对称
 关于点
关于点 对称
对称  关于直线
关于直线 对称
对称
 (
( 广东文)已知简谐运动
广东文)已知简谐运动 的图象经过点
的图象经过点 ,则该简谐运动的最小正周期
,则该简谐运动的最小正周期 和初相
和初相 分别为
分别为

 ,
, ;
;
 ,
, ;
;
 ,
, ;
;
 ,
,
 (
( 陕西)已知函数
陕西)已知函数
(Ⅰ)求函数 的最小正周期;(Ⅱ)求使函数
的最小正周期;(Ⅱ)求使函数 取得最大值的
取得最大值的 集合.
集合.
 (
( 全国Ⅰ文)设函数
全国Ⅰ文)设函数 图像的一条对称轴是直线
图像的一条对称轴是直线 .(Ⅰ)求
.(Ⅰ)求 ;(Ⅱ)求函数
;(Ⅱ)求函数 的单调增区间;
的单调增区间;
(Ⅲ)画出函数 在区间
在区间 上的图像。
上的图像。
 (
( 全国)已知函数
全国)已知函数
 是
是 上的偶函数,其图象关于点
上的偶函数,其图象关于点 对称,且在区间
对称,且在区间 上是单调函数。求
上是单调函数。求 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com