
 函数解析式的求解;
函数解析式的求解; 函数定义域的求解.
函数定义域的求解.
 (
( 全国Ⅰ)设
全国Ⅰ)设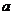 是实数,且
是实数,且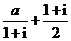 是实数,则
是实数,则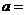

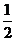

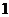

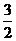

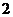
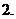 (
( 全国Ⅱ)设复数
全国Ⅱ)设复数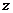 满足
满足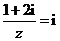 ,则
,则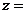

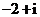



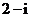

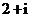
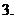 (
( 北京)
北京)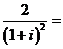
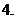 (
( 福建)复数
福建)复数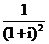 等于
等于

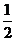

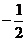

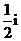

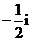
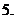 (
( 安徽)若
安徽)若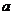 为实数,
为实数,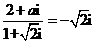 ,则
,则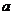 等于
等于

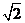

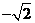

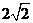

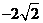
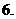 (
( 天津)是虚数单位,
天津)是虚数单位,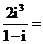

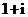

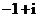

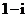

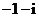
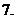 (
( 四川)复数
四川)复数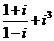 的值是
的值是

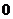

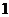

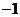

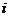
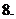 (
( 江西)化简
江西)化简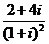 的结果是
的结果是

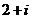

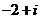

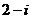

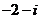
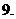 (
( 湖南)复数
湖南)复数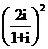 等于
等于

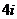

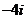

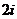

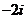
 (
( 湖北)复数
湖北)复数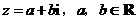 ,且
,且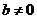 ,若
,若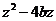 是实数,则有序实数对
是实数,则有序实数对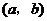 可以是
(写出一个有序实数对即可)
可以是
(写出一个有序实数对即可)
 (
( 上海,
上海,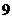 )对于非零实数
)对于非零实数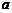 、
、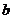 ,以下四个命题都成立:
,以下四个命题都成立:
① 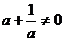 ;
②
;
② 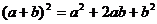 ;
;
③ 若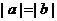 ,则
,则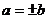 ; ④ 若
; ④ 若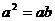 ,则
,则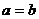 .
.
那么,对于非零复数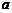 、
、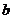 ,仍然成立的命题的所有序号是
,仍然成立的命题的所有序号是
 (
( 重庆)复数
重庆)复数 的虚部为
的虚部为
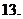 (
( 浙江)已知复数
浙江)已知复数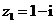 ,
,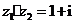 ,则复数
,则复数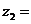
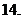 (
(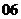 上海)若复数
上海)若复数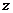 同时满足
同时满足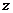 -
-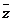 =
=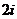 ,
,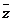 =
=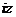 (
(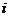 为虚数单位),则
为虚数单位),则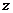 =
=
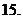 (
( 浙江)已知
浙江)已知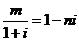 ,其中
,其中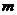 、
、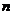 是实数,
是实数,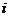 是虚数单位,则
是虚数单位,则

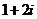

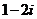

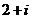

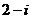
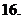 (
(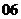 湖北)设
湖北)设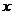 、
、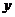 为实数,且
为实数,且 ,则
,则
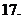 (
(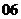 福建)设
福建)设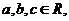 则复数
则复数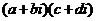 为实数的充要条件是( )
为实数的充要条件是( )

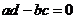

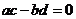

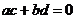

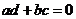
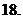 (
( 江西)已知复数
江西)已知复数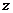 满足
满足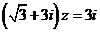 ,则
,则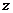 =
=

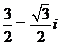

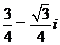

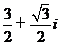

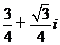
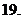 (
(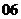 全国Ⅰ)如果复数
全国Ⅰ)如果复数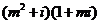 是实数,则实数
是实数,则实数

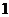

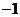

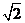

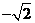
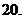 (
(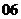 四川)复数
四川)复数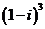 的虚部为
的虚部为

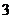

 .
. 
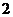

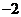
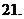 (
( 重庆)复数
重庆)复数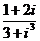 的值是
的值是
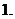 虚数单位
虚数单位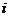 :
:
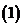 它的平方等于
它的平方等于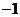 ,即
,即 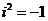 ;
;
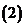 实数可以与它进行四则运算,进行四则运算时,原有加、乘运算律仍然成立.
实数可以与它进行四则运算,进行四则运算时,原有加、乘运算律仍然成立.
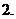
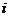 与-1的关系:
与-1的关系: 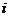 就是
就是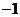 的一个平方根,即方程
的一个平方根,即方程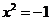 的一个根,方程
的一个根,方程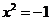 的另一个根是
的另一个根是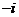 .
.
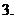
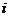 的周期性:
的周期性: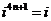 ,
, 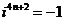 ,
,  ,
,  .
.
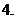 复数的定义:形如
复数的定义:形如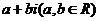 的数叫复数,
的数叫复数,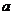 叫复数的实部,
叫复数的实部,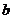 叫复数的虚部.全体复数所成的集合叫做复数集,用字母
叫复数的虚部.全体复数所成的集合叫做复数集,用字母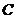 表示
表示
 复数的代数形式: 复数通常用字母
复数的代数形式: 复数通常用字母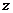 表示,即
表示,即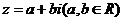 ,把复数表示成
,把复数表示成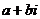 的形式,叫做复数的代数形式.
的形式,叫做复数的代数形式.
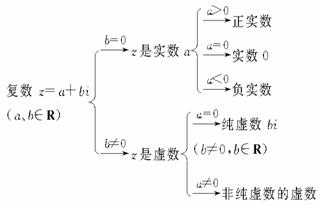
 复数与实数、虚数、纯虚数及
复数与实数、虚数、纯虚数及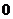 的关系:对于复数
的关系:对于复数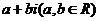 ,当且仅当
,当且仅当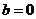 时,复数
时,复数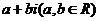 是实数
是实数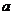 ;当
;当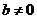 时,复数
时,复数 叫做虚数;当
叫做虚数;当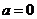 且
且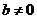 时,
时,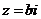 叫做纯虚数;当且仅当
叫做纯虚数;当且仅当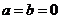 时,
时,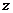 就是实数
就是实数
 复数集与其它数集之间的关系:
复数集与其它数集之间的关系: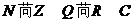
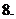 两个复数相等的定义:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.这就是说,如果
两个复数相等的定义:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.这就是说,如果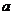 ,
,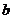 ,
,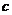 ,
,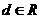 ,那么
,那么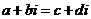
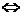
 ,
,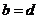
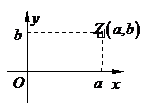
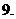 复平面、实轴、虚轴:复数
复平面、实轴、虚轴:复数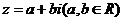 与有序实数
与有序实数
对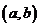 是一一对应关系.建立一一对应的关系.点
是一一对应关系.建立一一对应的关系.点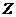 的横坐标是
的横坐标是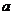 ,
,
纵坐标是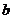 ,复数
,复数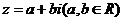 可用点
可用点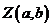 表示,这个
表示,这个
建立了直角坐标系来表示复数的平面叫做复平面,也叫高斯平面,
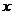 轴叫做实轴,
轴叫做实轴,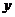 轴叫做虚轴.实轴上的点都表示实数.
轴叫做虚轴.实轴上的点都表示实数.
对于虚轴上的点要除原点外,因为原点对应的有序实数对为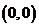 , 它所确定的复数是
, 它所确定的复数是 表示是实数.故除了原点外,虚轴上的点都表示纯虚数.
表示是实数.故除了原点外,虚轴上的点都表示纯虚数.
复数
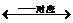 复平面内的点
复平面内的点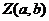
这就是复数的一种几何意义.也就是复数的另一种表示方法,即几何表示方法.
 复数
复数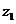 与
与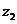 的和的定义:
的和的定义: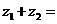
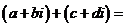
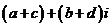
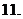 复数
复数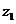 与
与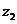 的差的定义:
的差的定义: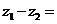
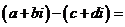
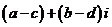
 复数的加法运算满足交换律:
复数的加法运算满足交换律: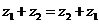
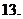 复数的加法运算满足结合律:
复数的加法运算满足结合律: 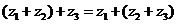
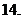 乘法运算规则:
乘法运算规则:
设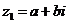 ,
,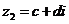 (
(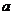 、
、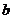 、
、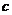 、
、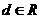 )是任意两个复数,那么它们的积
)是任意两个复数,那么它们的积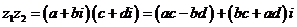
其实就是把两个复数相乘,类似两个多项式相乘,在所得的结果中把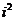 换成
换成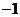 ,并且把实部与虚部分别合并.两个复数的积仍然是一个复数.
,并且把实部与虚部分别合并.两个复数的积仍然是一个复数.
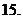 乘法运算律:
乘法运算律:
(1)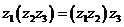
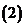
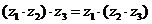
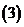
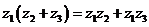
 复数除法定义:满足
复数除法定义:满足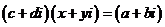 的复数
的复数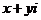 (
(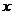 、
、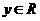 )叫复数
)叫复数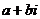 除以复数
除以复数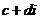 的商,记为:
的商,记为: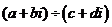 或者
或者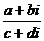
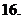 除法运算规则:
除法运算规则:
①设复数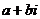 (
(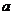 、
、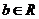 ),除以
),除以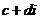 (
(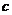 ,
,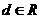 ),其商为
),其商为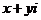 (
(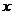 、
、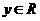 ),
),
即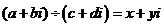 ∵
∵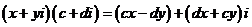
∴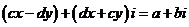
由复数相等定义可知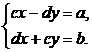 解这个方程组,得
解这个方程组,得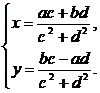
于是有: 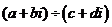
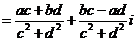
②利用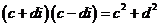 于是将
于是将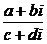 的分母有理化得:
的分母有理化得:
原式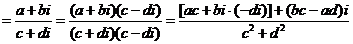
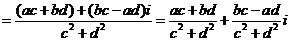 .
.
∴(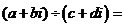
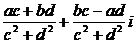
点评:①是常规方法,②是利用初中我们学习的化简无理分式时,都是采用的分母有理化思想方法,而复数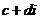 与复数
与复数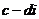 ,相当于我们初中学习的
,相当于我们初中学习的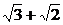 的对偶式
的对偶式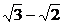 ,它们之积为
,它们之积为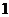 是有理数,而
是有理数,而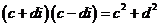 是正实数.所以可以分母实数化. 把这种方法叫做分母实数化法.
是正实数.所以可以分母实数化. 把这种方法叫做分母实数化法.
 共轭复数:当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数。虚部不等于
共轭复数:当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数。虚部不等于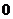 的两个共轭复数也叫做共轭虚数.
的两个共轭复数也叫做共轭虚数.
 (
( 陕西)
陕西) 是定义在
是定义在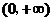 上的非负可导函数,且满足
上的非负可导函数,且满足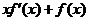 ≤
≤ .
.
对任意正数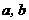 ,若
,若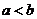 ,则必有
,则必有

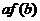 ≤
≤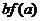

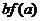 ≤
≤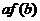

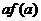 ≤
≤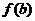

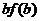 ≤
≤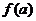
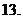 (
( 江苏)已知二次函数
江苏)已知二次函数 的导数为
的导数为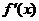 ,
, ,对于任意实数
,对于任意实数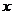 ,有
,有 ≥
≥ ,则
,则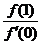 的最小值为
的最小值为 
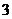

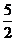

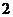

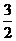
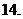 (
( 全国)函数
全国)函数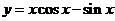 在下面哪个区间内是增函数
在下面哪个区间内是增函数

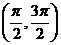

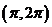

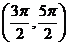

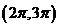
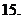 (
( 重庆)曲线
重庆)曲线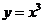 在点
在点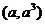
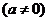 处的切线与
处的切线与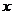 轴、直线
轴、直线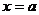 所围成的三角形的面积为
所围成的三角形的面积为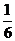 ,则
,则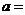
 (
(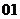 全国)已知
全国)已知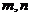 是正整数且
是正整数且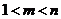 ,求证:
,求证: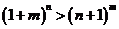
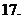 (
( 重庆)已知函数
重庆)已知函数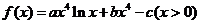 在
在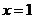 处取得极值
处取得极值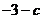 ,其中
,其中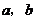 为常数.(Ⅰ)试确定
为常数.(Ⅰ)试确定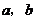 的值;(Ⅱ)讨论函数
的值;(Ⅱ)讨论函数 的单调区间;
的单调区间;
(Ⅲ)若对任意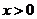 ,不等式
,不等式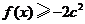 恒成立,求
恒成立,求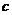 的取值范围.
的取值范围.
 (
( 海南)设函数
海南)设函数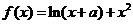
(Ⅰ)若当 时,
时, 取得极值,求
取得极值,求 的值,并讨论
的值,并讨论 的单调性;
的单调性;
(Ⅱ)若 存在极值,求
存在极值,求 的取值范围,并证明所有极值之和大于
的取值范围,并证明所有极值之和大于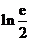 .
.
 (
( 全国Ⅰ)设函数
全国Ⅰ)设函数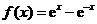 .
.
(Ⅰ)证明: 的导数
的导数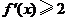 ;
;
(Ⅱ)若对所有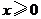 都有
都有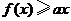 ,求
,求 的取值范围.
的取值范围.
 (
( 全国Ⅱ文)若函数
全国Ⅱ文)若函数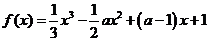 在区间
在区间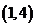 内为减函数,在区间
内为减函数,在区间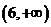 内为增函数,试求实数
内为增函数,试求实数 的取值范围.
的取值范围.
 已知函数
已知函数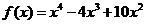 ,则方程
,则方程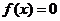 在区间
在区间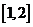 上的根有
上的根有

 个
个

 个
个

 个
个 
 个
个
 (
( 郑州一中等四校联考)若函数
郑州一中等四校联考)若函数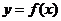 在
在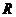 上可导且满足不等式
上可导且满足不等式
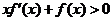 恒成立,且常数
恒成立,且常数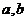 满足
满足 ,则下列不等式一定成立的是
,则下列不等式一定成立的是

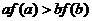

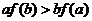

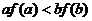

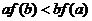
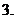 求满足条件的
求满足条件的 的范围:
的范围:
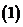 使
使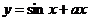 为
为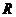 上增函数,则
上增函数,则 的范围是
的范围是
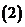 使
使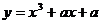 为
为 上增函数,则
上增函数,则 的范围是
的范围是
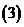 使
使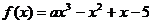 为
为 上增函数,则
上增函数,则 的范围是
的范围是
 证明方程
证明方程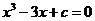 在
在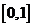 上至多有一实根.
上至多有一实根.
 (
( 届高三陕师大附中八模)如果
届高三陕师大附中八模)如果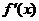 是二次函数, 且
是二次函数, 且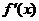 的图象开口向上,
的图象开口向上,
顶点坐标为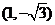 , 那么曲线
, 那么曲线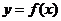 上任一点的切线的倾斜角
上任一点的切线的倾斜角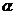 的取值范围是
的取值范围是

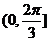



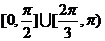

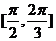
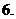 (
( 届厦门双十中学高三月考)如图,是函数
届厦门双十中学高三月考)如图,是函数
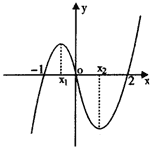
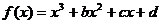 的大致图像,
的大致图像,
|
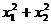 等于
等于

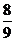

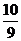

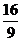


 (
(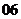 天津)函数
天津)函数 的定义域是开区间
的定义域是开区间 ,
,
导函数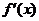 在
在 内的图象如图所示,则函数
内的图象如图所示,则函数
 在开区间内有极小值点
在开区间内有极小值点
 个
个 
 个
个 
 个
个 
 个
个
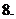 (
( 届高三哈尔滨第三中学第一次月考)
届高三哈尔滨第三中学第一次月考)
函数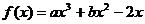 的图象如图所示,
的图象如图所示,
且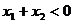 ,则有
,则有

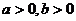

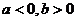

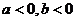

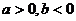
 已知:
已知: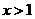 ,证明不等式:
,证明不等式: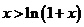
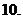 设
设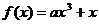 恰有三个单调区间,试确定
恰有三个单调区间,试确定 的取值范围,并求出这三个单调区间
的取值范围,并求出这三个单调区间
 (
( 届高三福建质检)已知函数
届高三福建质检)已知函数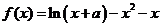 在
在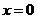 处取得极值.
处取得极值. 求实数
求实数 的值;
的值;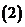 若关于
若关于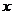 的方程
的方程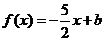 在区间
在区间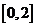 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数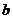 的取值范围;
的取值范围;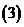 证明:对任意的正整数
证明:对任意的正整数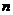 ,不等式
,不等式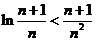 都成立.
都成立.
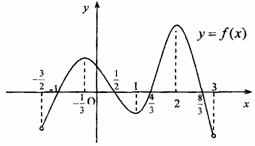
问题1. (
( 届云南平远一中五模)函数
届云南平远一中五模)函数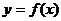 在定义域
在定义域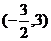 内可导,其图象如图所示,记
内可导,其图象如图所示,记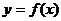 的导函数为
的导函数为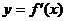 ,则不等式
,则不等式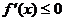 的解集为
的解集为

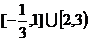

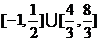

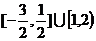


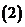 已知
已知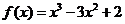 ,
,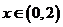 的反函数为
的反函数为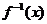 ,则
,则

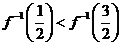

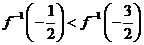

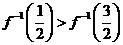


 (
( 大连一模)设
大连一模)设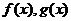 均是定义在
均是定义在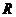 上的奇函数,当
上的奇函数,当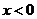 时,
时,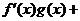
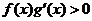 ,且
,且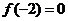 ,则不等式
,则不等式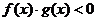 的解集是
的解集是

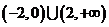

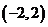

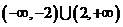

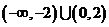
问题2. 如果函数
如果函数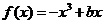 在区间
在区间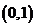 上单调递增,并且方程
上单调递增,并且方程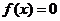 的根都在区间
的根都在区间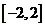 内,则
内,则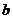 的取值范围为
的取值范围为
 (
( 届高三浙江上虞市调研)已知
届高三浙江上虞市调研)已知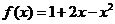 ,那么
,那么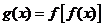
 在区间
在区间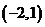 上单调递增
上单调递增  在
在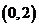 上单调递增
上单调递增
 在
在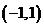 上单调递增
上单调递增
 在
在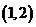 上单调递增
上单调递增
 函数
函数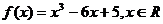 ,
,
(Ⅰ)求 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若关于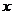 的方程
的方程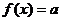 有
有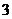 个不同实根,求实数
个不同实根,求实数 的取值范围.
的取值范围.
(Ⅲ)已知当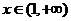 时,
时, ≥
≥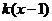 恒成立,求实数
恒成立,求实数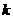 的取值范围.
的取值范围.
问题3.(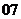 天津)已知函数
天津)已知函数
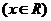 ,其中
,其中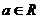 .
.
(Ⅰ)当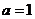 时,求曲线
时,求曲线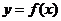 在点
在点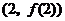 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求函数
时,求函数 的单调区间与极值.
的单调区间与极值.
问题4.(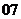 湖北)已知定义在正实数集上的函数
湖北)已知定义在正实数集上的函数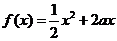 ,
, ,其中
,其中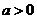 .设两曲线
.设两曲线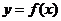 ,
,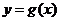 有公共点,且在该点处的切线相同.(Ⅰ)用
有公共点,且在该点处的切线相同.(Ⅰ)用 表示
表示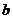 ,并求
,并求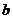 的最大值;(Ⅱ)求证:
的最大值;(Ⅱ)求证: ≥
≥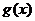 (
(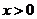 ).
).
问题5.利用导数求和:
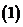
 (
(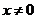 ,
, 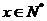 ).
).
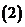
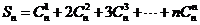 (
(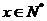 ).
).
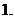 利用导数研究多项式函数单调性的一般步骤:
利用导数研究多项式函数单调性的一般步骤:
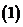 求
求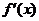 ;
;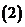 确定
确定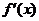 在
在 内符号;
内符号;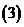 若
若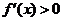 在
在 上恒成立,则
上恒成立,则 在
在 上是增函数;若
上是增函数;若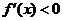 在
在 上恒成立,则
上恒成立,则 在
在 上是减函数
上是减函数
①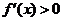
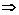
 为增函数(
为增函数(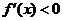
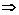
 为减函数).
为减函数).
② 在区间
在区间 上是增函数
上是增函数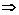
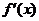 ≥
≥ 在
在 上恒成立;
上恒成立;
 在区间
在区间 上为减函数
上为减函数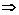
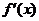 ≤
≤ 在
在 上恒成立.
上恒成立.
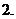 极大值: 一般地,设函数
极大值: 一般地,设函数 在点
在点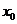 附近有定义,如果对
附近有定义,如果对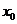 附近的所有的点,都有
附近的所有的点,都有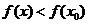 ,就说
,就说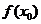 是函数
是函数 的一个极大值,记作
的一个极大值,记作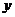 极大值
极大值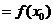 ,
,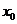 是极大值点.
是极大值点.
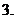 极小值:一般地,设函数
极小值:一般地,设函数 在
在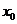 附近有定义,如果对
附近有定义,如果对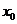 附近的所有的点,都有
附近的所有的点,都有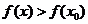 就说
就说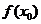 是函数
是函数 的一个极小值,记作
的一个极小值,记作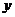 极小值
极小值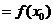 ,
,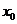 是极小值点.
是极小值点.
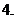 极大值与极小值统称为极值
极大值与极小值统称为极值
在定义中,取得极值的点称为极值点,极值点是自变量的值,极值指的是函数值 请注意以下几点:
请注意以下几点:
(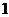 )极值是一个局部概念
)极值是一个局部概念 由定义,极值只是某个点的函数值与它附近点的函数值比较是最大或最小.并不意味着它在函数的整个的定义域内最大或最小.
由定义,极值只是某个点的函数值与它附近点的函数值比较是最大或最小.并不意味着它在函数的整个的定义域内最大或最小.
(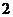 )函数的极值不是唯一的
)函数的极值不是唯一的 即一个函数在某区间上或定义域内极xs大值或极小值可以不止一个.
即一个函数在某区间上或定义域内极xs大值或极小值可以不止一个.
(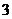 )极大值与极小值之间无确定的大小关系
)极大值与极小值之间无确定的大小关系 即一个函数的极大值未必大于极小值,如下图所示,
即一个函数的极大值未必大于极小值,如下图所示,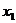 是极大值点,
是极大值点,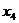 是极小值点,而
是极小值点,而 >
>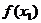 .
.
( )函数的极值点一定出现在区间的内部,区间的端点不能成为极值点
)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点 而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点.
而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点.
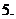 当
当 在点
在点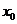 连续时,判别
连续时,判别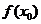 是极大、极小值的方法:
是极大、极小值的方法:
若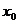 满足
满足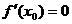 ,且在
,且在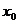 的两侧
的两侧 的导数异号,则
的导数异号,则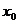 是
是 的极值点,
的极值点,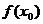 是极值,并且如果
是极值,并且如果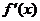 在
在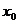 两侧满足“左正右负”,则
两侧满足“左正右负”,则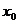 是
是 的极大值点,
的极大值点,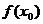 是极大值;如果
是极大值;如果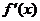 在
在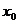 两侧满足“左负右正”,则
两侧满足“左负右正”,则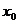 是
是 的极小值点,
的极小值点,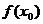 是极小值.
是极小值.
 求可导函数
求可导函数 的极值的步骤:
的极值的步骤:
 确定函数的定义区间,求导数
确定函数的定义区间,求导数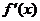
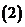 求方程
求方程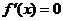 的根
的根
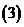 用函数的导数为
用函数的导数为 的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查
的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查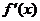 在方程根左右的值的符号,如果左正右负,那么
在方程根左右的值的符号,如果左正右负,那么 在这个根处取得极大值;如果左负右正,那么
在这个根处取得极大值;如果左负右正,那么 在这个根处取得极小值;如果左右不改变符号,那么
在这个根处取得极小值;如果左右不改变符号,那么 在这个根处无极值.如果函数在某些点处连续但不可导,也需要考虑这些点是否是极值点 .
在这个根处无极值.如果函数在某些点处连续但不可导,也需要考虑这些点是否是极值点 .
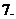 函数的最大值和最小值: 一般地,在闭区间
函数的最大值和最小值: 一般地,在闭区间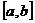 上连续的函数
上连续的函数 在
在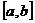 上必有最大值与最小值.
上必有最大值与最小值.
说明: 在开区间
在开区间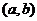 内连续的函数
内连续的函数 不一定有最大值与最小值.如函数
不一定有最大值与最小值.如函数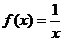 在
在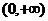 内连续,但没有最大值与最小值;
内连续,但没有最大值与最小值;
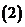 函数的最值是比较整个定义域内的函数值得出的;函数的极值是比较极值点附近函数值得出的.
函数的最值是比较整个定义域内的函数值得出的;函数的极值是比较极值点附近函数值得出的.
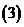 函数
函数 在闭区间
在闭区间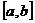 上连续,是
上连续,是 在闭区间
在闭区间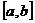 上有最大值与最小值的充分条件而非必要条件.
上有最大值与最小值的充分条件而非必要条件.
 函数在其定义区间上的最大值、最小值最多各有一个,而函数的极值可能不止一个,也可能没有一个.
函数在其定义区间上的最大值、最小值最多各有一个,而函数的极值可能不止一个,也可能没有一个.
 利用导数求函数的最值步骤:
利用导数求函数的最值步骤:
由上面函数 的图象可以看出,只要把连续函数所有的极值与定义区间端点的函数值进行比较,就可以得出函数的最值了.
的图象可以看出,只要把连续函数所有的极值与定义区间端点的函数值进行比较,就可以得出函数的最值了.
设函数 在
在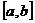 上连续,在
上连续,在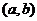 内可导,则求
内可导,则求 在
在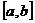 上的最大值与最小值的步骤如下:
上的最大值与最小值的步骤如下: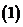 求
求 在
在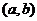 内的极值;
内的极值;
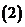 将
将 的各极值与
的各极值与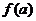 、
、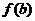 比较得出函数
比较得出函数 在
在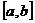 上的最值
上的最值 p
p
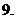 求参数范围的方法:①分离变量法;②构造(差)函数法.
求参数范围的方法:①分离变量法;②构造(差)函数法.
 构造函数法是证明不等式的常用方法:构造时要注意四变原则:变具体为抽象,变常量为变量,变主元为辅元,变分式为整式.
构造函数法是证明不等式的常用方法:构造时要注意四变原则:变具体为抽象,变常量为变量,变主元为辅元,变分式为整式.
 通过求导求函数不等式的基本思路是:以导函数和不等式为基础,单调性为主线,最(极值)为助手,从数形结合、分类讨论等多视角进行综合探索.
通过求导求函数不等式的基本思路是:以导函数和不等式为基础,单调性为主线,最(极值)为助手,从数形结合、分类讨论等多视角进行综合探索.
 (
( 陕西)为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文
陕西)为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文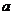 、
、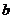 、
、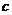 、
、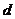 对应密文
对应密文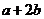 ,
,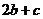 ,
,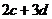 ,
,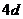 .例如:明文
.例如:明文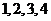 对应密文
对应密文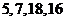 .当接收方收到密文
.当接收方收到密文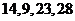 时,则解密得到的明文为
时,则解密得到的明文为



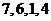




 (
( 浙江)函数
浙江)函数 :
: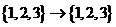 满足
满足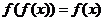 ,则这样的函数个数
,则这样的函数个数
共有 
 个
个 
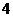 个
个 
 个
个 
 个
个
 (
( 广东文)对于任意的两个实数对
广东文)对于任意的两个实数对 和
和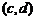 ,规定:
,规定: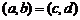 ,
,
当且仅当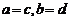 ;运算“
;运算“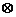 ”为:
”为: ;
;
运算“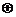 ”为:
”为: ,设
,设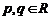 ,若
,若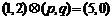 ,
,
则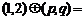



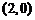

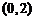

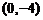
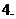 (
(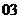 全国)已知
全国)已知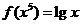 ,则
,则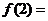 (
)
(
)

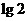

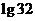

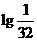

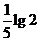
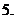 (
(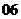 山东文)设
山东文)设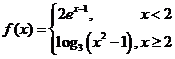 ,则
,则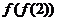 的值为
的值为








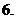 (
( 北京)已知函数
北京)已知函数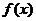 ,
, 分别由下表给出:
分别由下表给出:
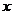







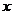



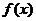



则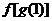 的值为 ;满足
的值为 ;满足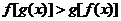 的
的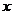 的值是
的值是
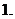
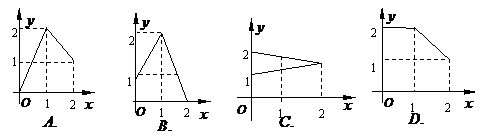 设
设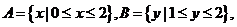 在下图中,能表示从集合
在下图中,能表示从集合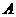 到集合
到集合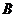 的映射是
的映射是
 已知从集合
已知从集合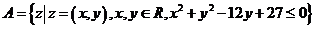 到集合
到集合 的映射
的映射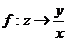 ,则该映射的象集为
,则该映射的象集为



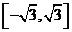

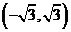
 以上都不对
以上都不对
 (
( 北京东城模拟)设映射
北京东城模拟)设映射 :
: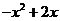 是实数集
是实数集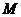 到实数集
到实数集 的映射,若对于实数
的映射,若对于实数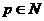 ,在
,在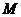 中不存在原象,则
中不存在原象,则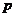 的取值范围是
的取值范围是
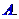
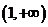

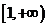

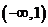

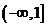
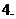 设集合
设集合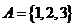 ,
,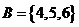 ,定义映射
,定义映射 :
: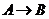 ,使对任意
,使对任意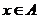 ,都有
,都有 是奇数,则这样的映射
是奇数,则这样的映射 的个数为
的个数为




 若
若 ,则
,则 )
)






 已知
已知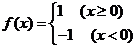 ,则不等式
,则不等式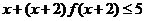 的解集是
的解集是
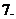 设
设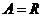 ,
, ,
, :
: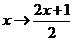 是
是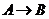 的映射,
的映射,
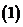 设
设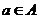 ,则
,则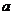 在
在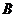 中的象是什么?
中的象是什么?
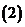 设
设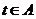 ,那么
,那么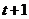 在
在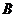 中的象是什么?
中的象是什么?
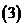 设
设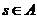 ,若
,若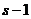 在映射
在映射 下的象为
下的象为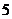 ,则
,则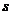 应是多少?
应是多少?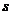 在映射
在映射 的象是什么?
的象是什么?
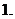
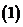
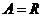 ,
,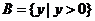 ,
,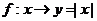 ;
;
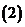
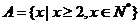 ,
,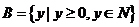 ,
, ;
;
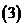
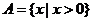 ,
,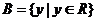 ,
,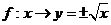 .
.
上述三个对应
是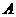 到
到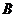 的映射.
的映射.
 给定映射
给定映射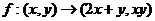 ,点
,点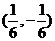 的原象是
的原象是
 下列函数中,与函数
下列函数中,与函数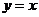 相同的函数是
相同的函数是

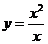

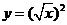

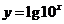

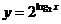
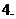 设函数
设函数 ,则
,则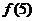 =
=
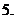 (
( 湖北八校一联)设
湖北八校一联)设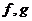 都是由
都是由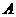 到
到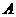 的映射,其对应法则如下表(从上到下):
的映射,其对应法则如下表(从上到下):
表一 映射 的对应法则
表二 映射
的对应法则
表二 映射 的对应法则
的对应法则
|
原象 |
 |
 |
 |
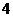 |
|
象 |
 |
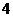 |
 |
 |
|
原象 |
 |
 |
 |
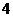 |
|
象 |
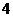 |
 |
 |
 |
则与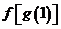 相同的是
相同的是 
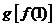

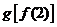

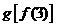

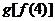
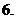 (
(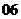 灌云模拟)设
灌云模拟)设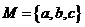 ,从
,从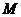 到
到 的映射
的映射 满足
满足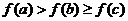 ,
,
试确定这样的映射 的个数为
的个数为 






湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com