
 (
( 广东)已知数列
广东)已知数列 的前
的前 项和
项和 ,第
,第 项满足
项满足 ,则
,则








 (
( 北京文)若数列
北京文)若数列 的前
的前 项和
项和
 ,则此数列的通项公式为
,则此数列的通项公式为
 (
( 江西)已知数列
江西)已知数列 对于任意
对于任意 ,有
,有 ,若
,若 ,则
,则

 (
( 全国)已知数列
全国)已知数列 的前
的前 项和
项和 满足
满足
 写出数列
写出数列 的前三项
的前三项 ;
;
 求数列
求数列 的通项公式;
的通项公式;
 (
( 全国Ⅰ)已知数列
全国Ⅰ)已知数列 中
中 ,且
,且 ,
,
其中 … (Ⅰ)求
… (Ⅰ)求 ,
, (Ⅱ)求
(Ⅱ)求 的通项公式.
的通项公式.
 (
( 全国)已知数列
全国)已知数列 ,满足
,满足 ,
, …
… ,则
,则 的通项
的通项
 (
( 天津)在数列
天津)在数列 中,
中, ,
, ,且
,且 ,
,
则
 已知数列
已知数列 中,
中, ,对所有的
,对所有的 ,都有
,都有 …
… ,则
,则








 数列
数列 中,
中, ,
, (
( ≥
≥ ),则
),则 等于
等于






 不存在
不存在
 数列
数列 中,
中, ,
, (
( ≥
≥ )求其通项公式.
)求其通项公式.
 数列
数列 满足
满足
 ,若
,若 ,则
,则 ;
;
 (
( 重庆)在数列
重庆)在数列 中,若
中,若 ,
, (
( ≥
≥ ),则该数列的通项
),则该数列的通项
 已知
已知
 ,则数列
,则数列 的最大项是
的最大项是





 或
或
 不存在
不存在
 (
( 南通市九校联考)已知数列
南通市九校联考)已知数列 中,
中,
 ,则在数列
,则在数列 的前
的前 项中最小项和最大项分别是
项中最小项和最大项分别是

 ,
,

 ,
,

 ,
,

 ,
,
 已知函数
已知函数 ,设数列
,设数列 满足:
满足: (
( 且
且 ),
), ,
,
 为数列
为数列 的前
的前 项和.
项和. 若
若 ,求
,求 ,
, ,
, ;
; 求证:数列
求证:数列 是周期数列;
是周期数列; 探究:是否存在满足
探究:是否存在满足 的
的 ,使
,使 ?
?
 已知
已知 ,则
,则
 在数列
在数列 中,
中, ,且
,且 ,则
,则
 在数列
在数列 中,
中, ,
, ,且
,且 ,则
,则
 (
( 湖南文)已知数列
湖南文)已知数列 满足
满足
 ,则
,则








 (
( 届高三湖南师大附中第二次月考)若数列
届高三湖南师大附中第二次月考)若数列 满足
满足 ,
, ,
,

 ,则
,则 等于
等于 








问题1. 根据下面各数列的前几项值,写出数列的一个通项公式:

 ,
, ,
, ,
, ,
, ,…;
,…; 
 ,
, ,
, ,
, ,
, ,…;
,…;

 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,…;
,…;
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,…;
,…;

 ,
, ,
, ,
, ,
, ,
, ,…;
,…; 
 ,
, ,
, ,
, ,
, ,…;
,…;

 ,
, ,
, ,
, ,
, ,…;
,…; 
 ,
, ,
, ,
, ,…;
,…;
问题2.根据下列各个数列 的首项和递推关系,求其通项公式:
的首项和递推关系,求其通项公式:

 ,
,
 ;
;
 ,
,
 ;
;

 ,
, ,
, ;
; 
 ,
,

问题3.已知下面各数列 的前
的前 项和
项和 ,求
,求 的通项公式:
的通项公式:

 ;
;


问题4. 求数列
求数列 中的最大项;
中的最大项;
 已知数列
已知数列 的通项公式
的通项公式 ,求
,求 为何值时,
为何值时, 取最大值.
取最大值.
问题5.设
 ,又知数列
,又知数列 的通项
的通项 满足
满足
 ,
, 试求数列
试求数列 的通项公式;
的通项公式; 判断数列
判断数列 的增减性.
的增减性.
数列通项公式的求法: 观察分析法;
观察分析法; 公式法:
公式法:
 转化成等差、等比数列;
转化成等差、等比数列; 累加、累乘法 ;
累加、累乘法 ; 递推法。
递推法。
 数列的有关概念;
数列的有关概念;
 数列的表示方法:
数列的表示方法: 列举法;
列举法; 图象法;
图象法; 解析法(通项公式);
解析法(通项公式); 递推法.
递推法.

 与
与 的关系:
的关系: .
.
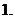 集合
集合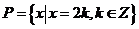 ,
,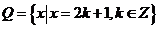 ,
,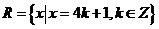 ,
,
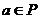 ,
,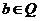 ,设
,设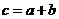 ,则有( )
,则有( )
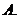
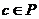
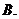
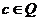
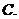
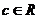
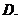 以上都不对
以上都不对
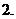 若
若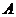 、
、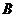 是全集
是全集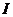 的真子集,则下列四个命题①
的真子集,则下列四个命题①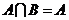 ;②
;②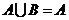 ;
;
③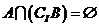 ;④
;④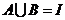 .中与命题
.中与命题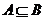 等价的有( )
等价的有( )
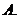
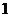 个
个
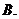
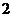 个
个
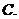
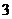 个
个 
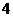 个
个
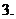 集合
集合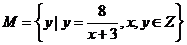 的元素个数是( )
的元素个数是( )
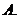
 个
个
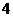 个
个 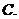
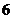 个
个
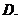
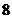 个
个
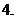 集合
集合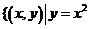 且
且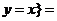

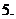 如图,
如图,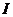 为全集,
为全集,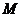 、
、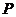 、
、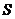 是
是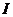 的三个子集,则阴影部分所表示的集合是( )
的三个子集,则阴影部分所表示的集合是( )
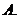
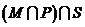
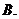
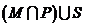
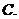
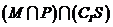
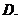
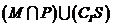
 已知集合
已知集合 ,
,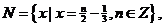
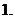 选择:集合
选择:集合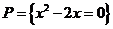 ( )、
( )、 ( )、
( )、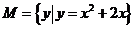 ( )、
( )、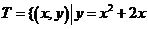 且
且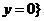 ( ).
( ).
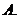
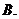
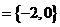
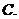
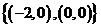
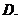 恰有一个元素
恰有一个元素 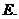
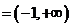
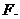

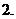 (
(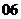 上海)已知集合
上海)已知集合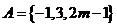 ,集合
,集合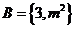 ,若
,若 ,则实数
,则实数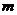 的值为
的值为
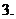 满足
满足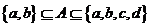 的集合
的集合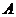 的个数有
个;
的个数有
个;
满足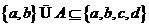 的集合
的集合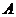 的个数有
个.
的个数有
个.
(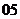 湖北)设
湖北)设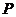 、
、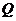 为两个非空实数集合,定义集合
为两个非空实数集合,定义集合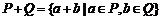 ,
,
若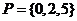 ,
, ,则
,则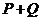 中元素的个数是( )
中元素的个数是( )
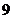
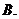
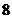
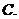
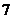
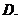
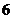
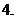 调查某班
调查某班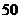 名学生,音乐爱好者
名学生,音乐爱好者 名,体育爱好者
名,体育爱好者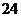 名,则两方面都爱好的人数最少是
,最多是
名,则两方面都爱好的人数最少是
,最多是
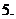
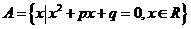
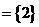 ,则
,则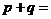
问题1:已知集合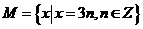 ,
,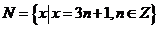 ,
,
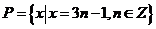 ,且
,且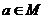 ,
,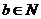 ,
,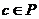 ,设
,设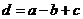 ,则
,则
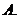
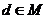
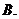
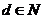
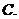
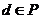
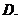
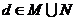
问题2:设集合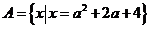 ,
,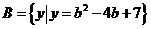 .
.
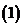 若
若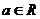 ,
,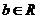 ,试确定集合
,试确定集合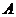 与集合
与集合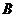 的关系;
的关系;
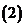 若
若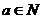 ,
,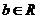 ,试确定集合
,试确定集合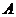 与集合
与集合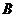 的关系.
的关系.
问题3: 年第
年第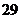 届奥运会将在北京召开,现有三个实数的集合,既可以表示
届奥运会将在北京召开,现有三个实数的集合,既可以表示
为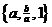 ,也可以表示为
,也可以表示为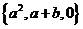 ,则
,则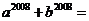
问题4:( 新课程)设
新课程)设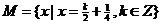 ,
, 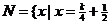 ,
,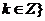
则
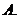

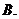

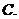
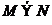
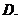
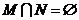
问题5:①若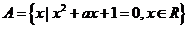 ,
, 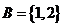 ,且
,且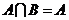 ,求
,求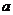 的范围
的范围
②设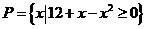 ,
,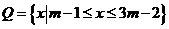 ,若
,若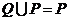 ,求
,求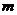 的范围
的范围
[机动]设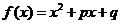 ,
,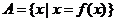 ,
,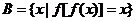 ,
,
(1)求证: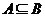 ;
;
(2)如果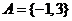 ,求
,求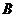 .
.
 解决集合问题,首先要弄清楚集合中的元素是什么,即元素分析法的掌握.
解决集合问题,首先要弄清楚集合中的元素是什么,即元素分析法的掌握.
 弄清集合中元素的本质属性,能化简的要化简;
弄清集合中元素的本质属性,能化简的要化简;
 抓住集合中元素的
抓住集合中元素的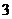 个性质,对互异性要注意检验;
个性质,对互异性要注意检验;
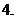 正确进行“集合语言”和普通“数学语言”的相互转化.
正确进行“集合语言”和普通“数学语言”的相互转化.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com