
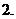 集合中元素的
集合中元素的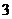 个性质,集合的
个性质,集合的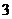 种表示方法;
种表示方法;
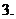 若有限集
若有限集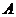 有
有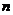 个元素,则
个元素,则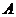 的子集有
的子集有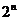 个,真子集有
个,真子集有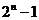 ,非空子集有
,非空子集有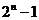 个,非空真子集有
个,非空真子集有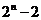 个.
个.
 空集是任何集合的子集,空集是任何非空集合的真子集.
空集是任何集合的子集,空集是任何非空集合的真子集.
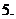 若
若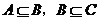 ,则
,则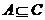
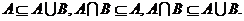
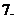
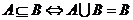 ;
;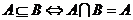 .
.
 (
( 北京春) 某服装厂生产一种服装,每件服装的成本为
北京春) 某服装厂生产一种服装,每件服装的成本为 元,出厂单价定为
元,出厂单价定为 元。该厂为鼓励销售商订购,决定当一次订购量超过
元。该厂为鼓励销售商订购,决定当一次订购量超过 件时,每多订购一件,订购的全部服装的出厂单价就降低
件时,每多订购一件,订购的全部服装的出厂单价就降低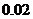 元。根据市场调查,销售商一次订购量不会超过
元。根据市场调查,销售商一次订购量不会超过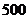 件。
件。
(Ⅰ)设一次订购量为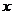 件,服装的实际出厂单价为
件,服装的实际出厂单价为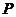 元,写出函数
元,写出函数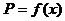 的表达式;
的表达式;
(Ⅱ)当销售商一次订购了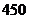 件服装时,该服装厂获得的利润是多少元?
件服装时,该服装厂获得的利润是多少元?
(服装厂售出一件服装的利润=实际出厂单价-成本)
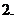 (
(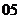 湖南文)某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为
湖南文)某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为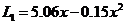 和
和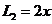 ,其中
,其中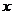 为销售量(单位:辆).若该公司在这两地共销售
为销售量(单位:辆).若该公司在这两地共销售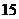 辆车,则能获得的最大利润为
辆车,则能获得的最大利润为
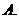
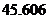
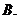
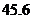
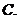
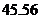
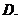
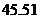
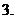
 (
(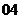 上海)某单位用木料制作如图所示的框架, 框架的下部是边长
上海)某单位用木料制作如图所示的框架, 框架的下部是边长
分别为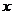 、
、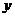 (单位:
(单位: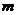 )的矩形.上部是等腰直角三角形. 要求
)的矩形.上部是等腰直角三角形. 要求
框架围成的总面积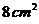 . 问
. 问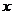 、
、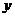 分别为多少(精确到
分别为多少(精确到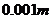 )
)
时用料最省?
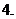 (
(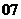 湖北文)某商品每件成本
湖北文)某商品每件成本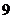 元,售价为
元,售价为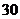 元,每星期卖出
元,每星期卖出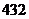 件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值
件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值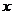 (单位:元,
(单位:元,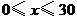 )的平方成正比,已知商品单价降低
)的平方成正比,已知商品单价降低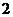 元时,一星期多卖出
元时,一星期多卖出 件.
件.
(Ⅰ)将一个星期的商品销售利润表示成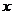 的函数;
的函数;
(Ⅱ)如何定价才能使一个星期的商品销售利润最大?
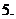 (
( 湖北文)为了预防流感,某学校对教室用药熏
湖北文)为了预防流感,某学校对教室用药熏
消毒法进行消毒.已知药物释放过程中,室内每立方米
空气中的含药量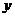 (毫克)与时间
(毫克)与时间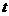 (小时)成正比;
(小时)成正比;
药物释放完毕后,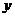 与
与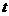 的函数关系式为
的函数关系式为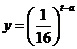
(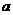 为常数),如图所示,根据图中提供的信息,
为常数),如图所示,根据图中提供的信息,
回答下列问题:
(Ⅰ)从药物释放开始,每立方米空气中的含药量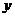
(毫克)与时间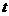 (小时)之间的函数关系式为
(小时)之间的函数关系式为
(Ⅱ)据测定,当空气中每立方米的含药量降低到
 毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过 小时后,学生才能回到教室.
毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过 小时后,学生才能回到教室.
问题1.(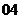 全国文)某村计划建造一个室内面积为
全国文)某村计划建造一个室内面积为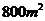 的矩形蔬菜温室。在温室内,沿左、右两侧与后侧内墙各保留
的矩形蔬菜温室。在温室内,沿左、右两侧与后侧内墙各保留 宽的通道,沿前侧内墙保留
宽的通道,沿前侧内墙保留 宽的空地。当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
宽的空地。当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
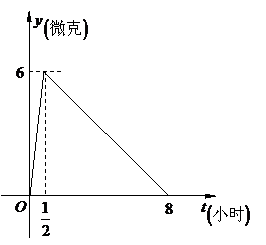 问题2.某医药研究所开发一种新药,如果成人按
问题2.某医药研究所开发一种新药,如果成人按
规定的剂量服用,据监测,服药后每毫升血液中的含药
量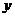 与时间
与时间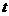 之间近似满足如图所示的曲线:
之间近似满足如图所示的曲线:
 写出服药后
写出服药后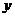 与
与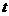 之间的函数关系式;
之间的函数关系式;
 据测定:每毫升血液中含药量不少于
据测定:每毫升血液中含药量不少于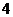 微克时
微克时
治疗疾病有效,假若某病人一天中第一次服药时间
为 ,问一天中怎样安排服药的时间、次数、
,问一天中怎样安排服药的时间、次数、
效果最佳?
 问题3.(
问题3.(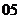 全国Ⅲ文)用长为
全国Ⅲ文)用长为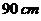 宽为
宽为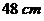 的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转
的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转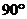 角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少?
角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少?
问题4.(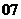 山东文)本公司计划
山东文)本公司计划 年在甲、乙两个电视台做总时间不超过
年在甲、乙两个电视台做总时间不超过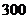 分钟的广告,广告总费用不超过
分钟的广告,广告总费用不超过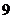 万元,甲、乙电视台的广告收费标准分别为
万元,甲、乙电视台的广告收费标准分别为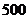 元/分钟和
元/分钟和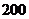 元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为
元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为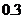 万元和
万元和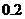 万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
问题5.(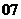 福建)某分公司经销某种品牌产品,每件产品的成本为
福建)某分公司经销某种品牌产品,每件产品的成本为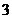 元,并且每件产品需向总公司交
元,并且每件产品需向总公司交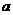 元(
元(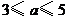 )的管理费,预计当每件产品的售价为
)的管理费,预计当每件产品的售价为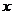 元(
元(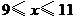 )时,一年的销售量为
)时,一年的销售量为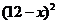 万件.
万件.
(Ⅰ)求分公司一年的利润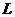 (万元)与每件产品的售价
(万元)与每件产品的售价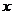 的函数关系式;
的函数关系式;
(Ⅱ)当每件产品的售价为多少元时,分公司一年的利润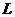 最大,并求出
最大,并求出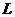 的最大值
的最大值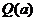 .
.
解数学应用题的一般步骤为: 审题;
审题; 建模;
建模; 求解;
求解; 作答.
作答.
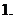 函数定义域、图象、单调性质等知识;
函数定义域、图象、单调性质等知识;
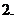 函数的值域、最值;解不等式等知识。
函数的值域、最值;解不等式等知识。
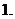 (
(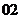 新课程)已知
新课程)已知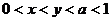 ,则有
,则有

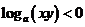

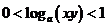

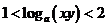

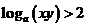
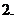 (
(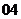 江苏)若函数
江苏)若函数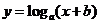
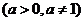 的图象过两点
的图象过两点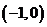 和
和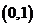 ,则
,则

 ,
,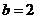

 ,
,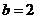

 ,
,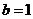

 ,
,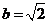
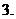 (
( 全国Ⅰ)若正整数
全国Ⅰ)若正整数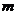 满足
满足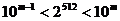 ,则
,则

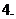 (
( 全国Ⅰ)设
全国Ⅰ)设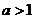 ,函数
,函数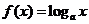 在区间
在区间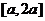 上的最大值与最小值之差为
上的最大值与最小值之差为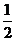 ,则
,则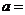

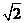



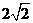

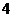
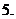 (
(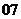 全国Ⅱ)下列四个数中最大的是( )
全国Ⅱ)下列四个数中最大的是( )

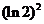

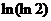

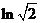

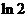
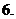 (
(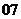 天津文)设
天津文)设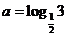 ,
,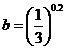 ,
,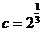 ,则( )
,则( )

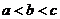

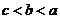

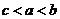

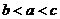
 (
( 天津文)若函数
天津文)若函数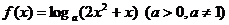 在区间
在区间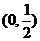 内恒有
内恒有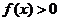 ,则
,则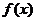 的单调递增区间为
的单调递增区间为

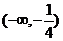

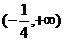

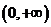

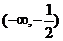
 (
( 天津)设
天津)设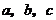 均为正数,且
均为正数,且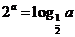 ,
,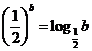 ,
,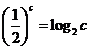 .则
.则
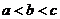

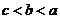

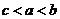

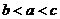
 (
( 浙江)已知
浙江)已知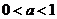 ,
,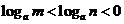 ,则
,则

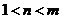

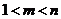

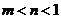

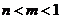
 (
( 辽宁文)设
辽宁文)设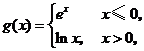 则
则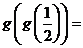
 (
( 辽宁文)方程
辽宁文)方程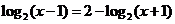 的解为
的解为
 (
( 重庆)函数
重庆)函数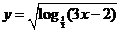 的定义域是
的定义域是 
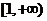

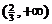

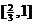

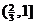
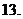 (
( 福建)已知函数
福建)已知函数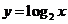 的反函数是
的反函数是 ,则函数
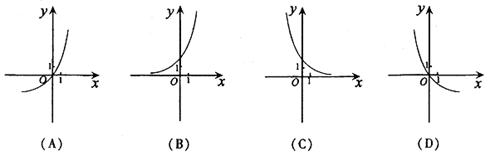
,则函数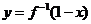 的图象是
的图象是
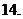 (
( 四川)函数
四川)函数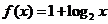 与
与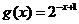 在同一直角坐标系下的图象大致是
在同一直角坐标系下的图象大致是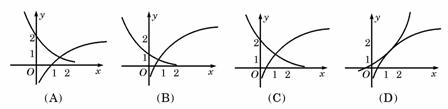
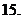 (
(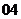 上海文)若函数
上海文)若函数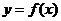 的图象与函数
的图象与函数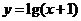 的图象关于直线
的图象关于直线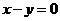 对称,则
对称,则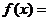

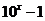

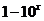

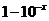

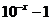
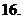 (
(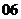 天津文)设
天津文)设 ,
,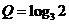 ,
,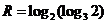 ,则
,则



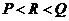

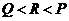

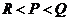
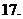 (
(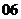 浙江文)已知
浙江文)已知 ,则
,则

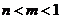

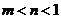

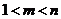

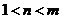
 (
( 浙江)已知
浙江)已知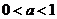 ,
,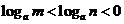 ,则
,则

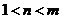

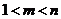

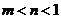

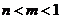
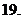 (
(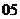 辽宁)若
辽宁)若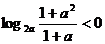 ,则
,则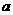 的取值范围是
的取值范围是

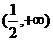

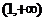

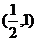

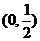
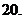 (
(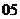 全国Ⅲ)若
全国Ⅲ)若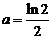 ,
,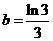 ,
,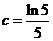 ,则
,则

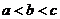

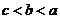

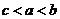

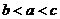
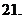 (
( 山东文)下列大小关系正确的是
山东文)下列大小关系正确的是

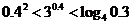 ;
; 
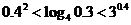 ;
;

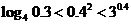 ;
; 
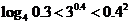
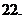 (
(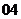 广东)函数
广东)函数
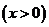 的反函数
的反函数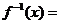
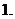 已知函数
已知函数 ,若
,若 ,则
,则 、
、 、
、 从小到大依次为
从小到大依次为
(注: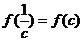 )
)
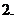 函数
函数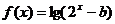 (
(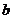 为常数),若
为常数),若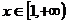 时,
时,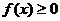 恒成立,则
恒成立,则

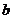 ≤
≤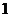

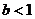
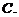
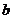 ≥
≥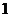

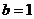
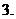
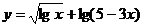 的定义域为
;
的定义域为
;
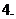
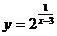 的值域为
;
的值域为
;
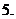
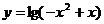 的递增区间为
,值域为
的递增区间为
,值域为
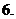
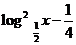 ≤
≤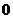 ,则
,则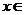
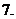 函数
函数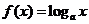
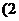 ≤
≤ ≤
≤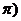 的最大值比最小值大
的最大值比最小值大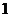 ,则
,则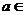
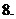 若
若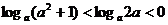 ,则
,则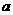 的取值范围是
的取值范围是

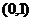

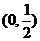
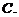
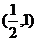

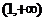
 已知
已知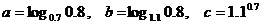 ,则
,则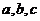 的大小关系是
的大小关系是

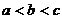



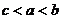

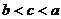
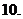 (
( 天津河西区模拟)若函数
天津河西区模拟)若函数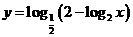 的值域是
的值域是

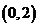

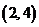

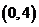

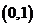
 已知函数
已知函数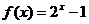 的反函数为
的反函数为
 若
若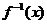 ≤
≤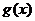 ,求
,求 的取值范围
的取值范围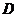 ;
;
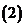 设
设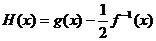 ,当
,当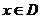 时,求函数
时,求函数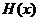 的值域
的值域
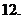 (
( 郑州质检)已知函数
郑州质检)已知函数

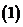 试判断
试判断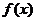 的奇偶性;
的奇偶性;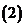 解不等式
解不等式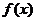 ≥
≥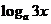
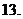 (
(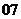 湖北八校联考)设
湖北八校联考)设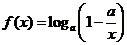 (
(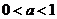 ).
).
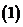 证明:
证明: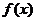 是
是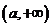 上的减函数;
上的减函数;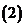 解不等式
解不等式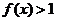
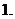 函数
函数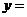
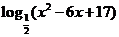 的值域是
的值域是

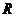

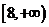

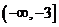

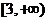
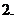 (
(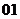 全国)若定义在区间
全国)若定义在区间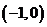 内的函数
内的函数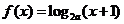 满足
满足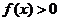 ,则
,则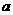 的
的
取值范围是

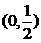

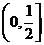

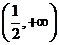

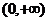
问题1.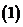 (
( 上海)若
上海)若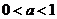 ,则函数
,则函数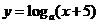 的图象不经过
的图象不经过
 第一象限
第一象限  第二象限
第二象限  第三象限
第三象限  第四象限
第四象限
( 安徽文)设
安徽文)设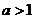 ,且
,且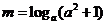 ,
,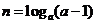 ,
,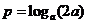 ,则
,则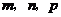 的大小关系为
的大小关系为

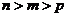

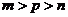

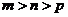

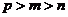
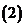 若函数
若函数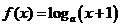 (
(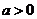 ,
,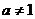 )的定义域和值域都是
)的定义域和值域都是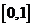 ,则
,则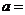

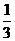

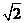

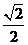


 若
若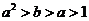 ,则
,则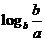 ,
,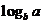 ,
,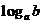 从小到大依次为
从小到大依次为
问题2.求下列函数的值域 :
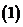
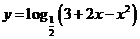 ;
;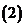
 (
( ≥
≥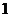 )
)
问题3.  (
( 江苏)不等式
江苏)不等式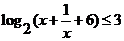 的解集为
的解集为
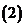 若不等式
若不等式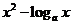 ≤
≤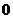 在
在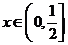 内恒成立,则
内恒成立,则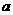 的取值范围是
的取值范围是

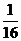 ≤
≤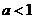

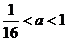

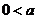 ≤
≤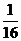

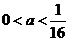
问题4.已知函数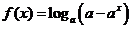 (
(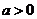 且
且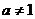 )
)
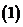 求
求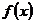 的定义域,值域;
的定义域,值域;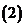 求证该函数的图象关于直线
求证该函数的图象关于直线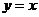 对称;
对称;
 解不等式
解不等式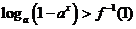
问题5. 设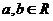 且
且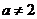 ,定义在区间
,定义在区间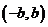 内的函数
内的函数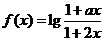 是奇函数.
是奇函数.
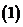 求
求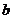 的取值范围;
的取值范围;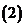 讨论函数
讨论函数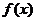 的单调性.
的单调性.
 解决与对数函数有关的问题,要特别重视定义域;
解决与对数函数有关的问题,要特别重视定义域;
 解决对数不等式、对数方程时,要重视考虑对数的真数、底数的范围;
解决对数不等式、对数方程时,要重视考虑对数的真数、底数的范围;
 对数不等式的主要解决思想是对数函数的单调性。
对数不等式的主要解决思想是对数函数的单调性。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com