
问题1.计算: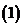
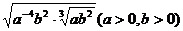 ;
;
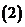
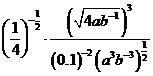
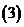
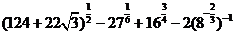

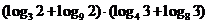 ;
;
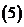
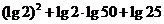 ;
;
问题2.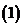 已知
已知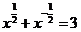 ,求
,求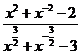 的值;
的值;
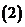


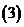 已知
已知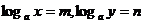 ,求
,求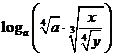 ;
;
问题3.已知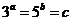 ,且
,且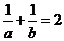 ,求
,求 的值.
的值.
问题4.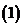 (
( 上海春)方程
上海春)方程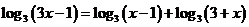 的解是
的解是
 (
( 上海)方程
上海)方程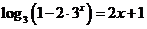 的解
的解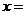
问题5.设 ,
,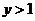 ,且
,且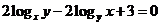 ,求
,求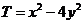 的最小值.
的最小值.
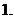 重视指数式与对数式的互化;
重视指数式与对数式的互化;
 根式运算时,常转化为分数指数幂,再按幂的运算法则运算;
根式运算时,常转化为分数指数幂,再按幂的运算法则运算;
 不同底的对数运算问题,应化为同底对数式进行运算;
不同底的对数运算问题,应化为同底对数式进行运算;
 运用指数、对数的运算公式解题时,要注意公式成立的前提.
运用指数、对数的运算公式解题时,要注意公式成立的前提.
 指数方程和对数方程按照不同类型的对应方法解决.
指数方程和对数方程按照不同类型的对应方法解决.
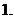
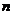 次方根的定义及性质:
次方根的定义及性质: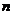 为奇数时,
为奇数时,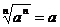 ,
,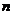 为偶数时,
为偶数时,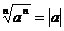 .
.
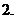 分数指数幂与根式的互化:
分数指数幂与根式的互化: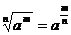 ,
,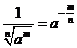 (
(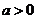 ,
,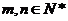 ,且
,且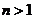 )
)
零的正分数指数幂为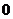 ,
,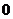 的负分数指数幂没有意义.
的负分数指数幂没有意义.
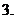 指数的运算性质:
指数的运算性质: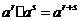 ,
,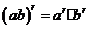 (其中
(其中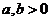 ,
,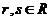 )
)
 指数式与对数式的互化:
指数式与对数式的互化: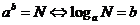 .
.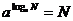 ,
,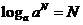 .
.
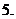 对数的运算法则:如果
对数的运算法则:如果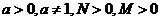 有
有
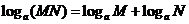 ;
; 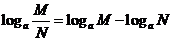 ;
;
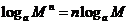 ;
; 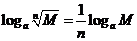
 换底公式及换底性质:
换底公式及换底性质:
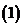
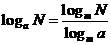 (
(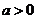 ,
,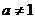 ,
,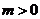 ,
, 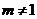 ,
,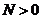 )
) 
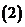
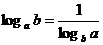 ,
,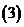
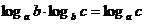 ,
, 
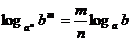
 指数方程和对数方程主要有以下几种类型:
指数方程和对数方程主要有以下几种类型:
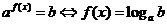 ;
;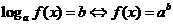 (定义法)
(定义法)
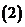
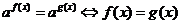 ;
;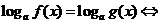
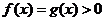 (同底法)
(同底法)
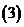
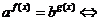
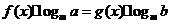 (两边取对数法)
(两边取对数法)


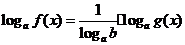 (换底法)
(换底法)
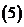
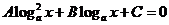 (
(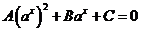 )(设
)(设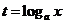 或
或 )(换元法)
)(换元法)
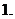

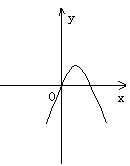
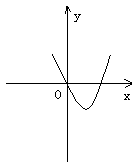
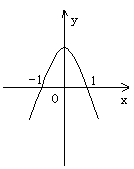 (
(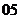 全国)设
全国)设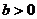 ,二次函数
,二次函数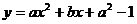 的图像为下列之一
的图像为下列之一
则 的值为
的值为
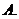
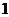
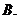

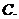
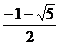
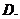
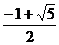
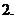 (
(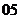 辽宁)在
辽宁)在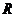 上定义运算
上定义运算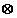 :
: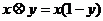 ,若不等式
,若不等式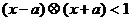
对任意实数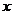 成立,则
成立,则 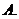
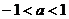
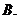
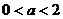
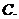
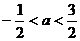
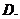
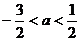
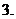 (
( 天津文)设
天津文)设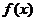 是定义在
是定义在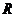 上的奇函数,且当
上的奇函数,且当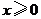 时,
时,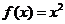 ,若对任意的
,若对任意的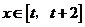 ,不等式
,不等式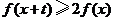 恒成立,则实数
恒成立,则实数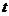 的取值范围是( )
的取值范围是( )
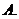
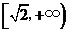
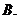
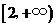
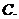
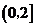
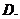
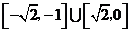
 (
( 陕西文)已知函数
陕西文)已知函数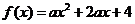
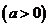 ,若
,若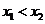 ,
,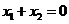 , 则
, 则
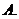
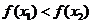
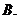

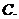
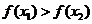
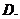
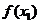 与
与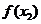 的大小不能确定
的大小不能确定
 (
( 陕西)若函数
陕西)若函数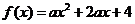 (
( ),且
),且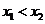 ,
,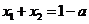 ,则
,则
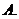
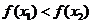
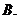

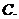
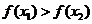
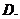
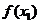 与
与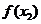 的大小不能确定
的大小不能确定
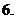
 (
( 湖南文)若函数
湖南文)若函数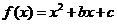 的图象的顶点在第四象限,则函数
的图象的顶点在第四象限,则函数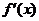 的图象是
的图象是
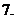 (
( 上海文)已知函数
上海文)已知函数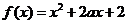 (
(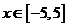 ).
).
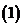 当
当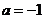 时,求函数
时,求函数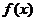 的最大值与最小值.
的最大值与最小值.
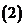 求实数
求实数 的取值范围,使
的取值范围,使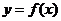 在区间
在区间 上是单调函数.
上是单调函数.
 (
( 福建)已知函数
福建)已知函数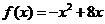 ,
,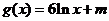
(Ⅰ)求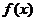 在区间
在区间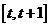 上的最大值
上的最大值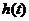 ;
;
(Ⅱ)是否存在实数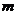 ,使得
,使得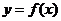 的图象与
的图象与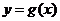 的图象有且只有三个不同的交点?若存在,求出
的图象有且只有三个不同的交点?若存在,求出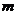 的取值范围;,若不存在,说明理由。
的取值范围;,若不存在,说明理由。
 (
( 湖北文)设二次函数
湖北文)设二次函数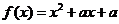 ,方程
,方程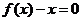 的两根
的两根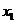 和
和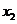 满足
满足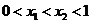 .
.
(Ⅰ)求实数 的取值范围;
的取值范围;
(Ⅱ)试比较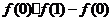 与
与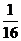 的大小.并说明理由.
的大小.并说明理由.
 (
( 福建文)设函数
福建文)设函数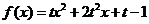
 .
.
(Ⅰ)求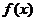 的最小值
的最小值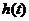 ;
;
(Ⅱ)若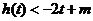 对
对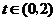 恒成立,求实数
恒成立,求实数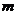 的取值范围.
的取值范围.
 (
(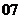 安徽文,
安徽文,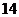 分)设函数
分)设函数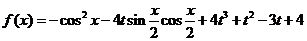 ,
,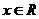 ,其中
,其中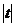 ≤
≤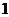 ,将
,将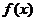 的最小值记为
的最小值记为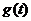 .
.
(Ⅰ)求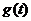 的表达式;
的表达式;
(Ⅱ)讨论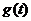 在区间
在区间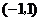 内的单调性并求极值.
内的单调性并求极值.
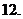 (
(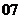 广东,
广东,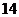 分)已知
分)已知 是实数,函数
是实数,函数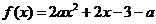 ,如果函数
,如果函数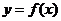 在区间
在区间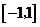 上有零点,求
上有零点,求 的取值范围.
的取值范围.
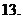 (
( 浙江文)设
浙江文)设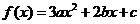 ,若
,若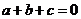 ,
,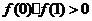
求证:(Ⅰ)方程 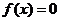 有实根。 (Ⅱ)
有实根。 (Ⅱ) 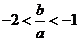 ;
;
(Ⅲ)设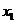 、
、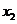 是方程
是方程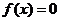 的两个实根,则
的两个实根,则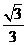 ≤
≤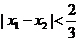
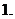 (
( 上海)若函数
上海)若函数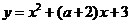 (
(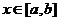 )的图象关于
)的图象关于 对称,
对称,
则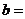
 若不等式
若不等式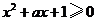 对一切
对一切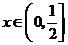 成立,则
成立,则 的最小值为( )
的最小值为( )
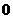
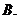
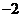
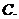
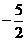
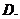
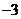
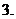 已知
已知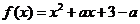 ,若
,若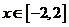 时
时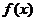 ≥
≥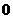 恒成立,则
恒成立,则 的范围是
的范围是
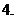 (
(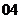 云南二检)已知实数
云南二检)已知实数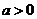 ,
,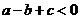 ,其中
,其中 、
、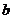 、
、 ,则一定有
,则一定有
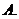

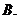
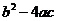 ≤
≤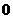
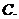
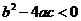
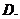
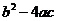 ≥
≥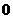
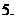 设
设 、
、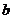 、
、 ,且
,且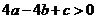 ,
, ,则下列结论中正确的是
,则下列结论中正确的是
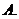
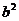 ≤
≤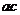
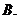
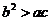
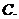
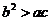 且
且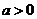
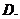
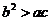 且
且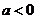
 已知函数
已知函数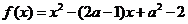 与非负
与非负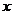 轴至少有一个交点,求
轴至少有一个交点,求 的范围.
的范围.
 关于
关于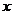 的方程
的方程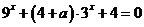 有实数解,则实数
有实数解,则实数 的范围是
的范围是
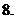
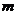 取何值时,方程
取何值时,方程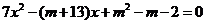 的一根大于
的一根大于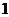 ,一根小于
,一根小于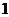 .
.
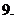 二次函数
二次函数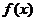 的二次项系数为负值,且
的二次项系数为负值,且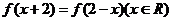 ,问
,问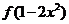 与
与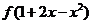 满足什么关系时,有
满足什么关系时,有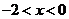 .
.
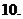 已知函数
已知函数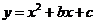 且
且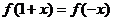 ,则下列不等式中成立的是
,则下列不等式中成立的是
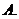
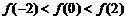
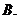
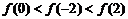
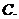
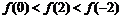
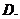
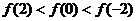
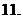 不等式
不等式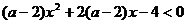 对一切
对一切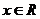 恒成立,则
恒成立,则 的范围是
的范围是
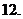 已知
已知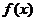 为二次函数,且
为二次函数,且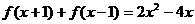 ,求
,求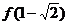 的值.
的值.
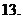 设函数
设函数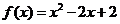 (
(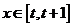 )的最小值为
)的最小值为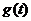 ,求
,求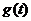 的解析式
的解析式
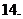 设函数
设函数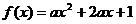 在
在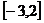 上有最大值
上有最大值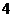 ,求实数
,求实数 的值。
的值。
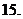 (
(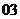 北京西城模拟)已知函数
北京西城模拟)已知函数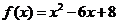 (
(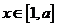 ),并且函数
),并且函数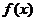 的最小值为
的最小值为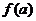 ,则实数
,则实数 的取值范围是
的取值范围是
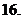 若不等式
若不等式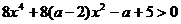 对一切实数
对一切实数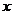 均成立,求实数
均成立,求实数 的取值范围
的取值范围
 已知函数
已知函数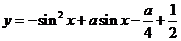 的最大值为
的最大值为 ,求
,求 的值
的值
 设函数
设函数 在区间
在区间 (
( 是正整数),那么
是正整数),那么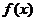 的值域中共有
的值域中共有
个整数.
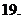 (
( 天津宝坻模拟)函数
天津宝坻模拟)函数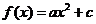 在
在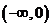 上单调递增,则
上单调递增,则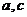 应满足
应满足
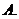
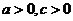
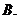
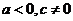
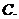
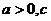 是任意实数
是任意实数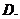
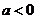 ,
,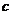 是任意实数
是任意实数
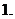 已知二次函数的对称轴为
已知二次函数的对称轴为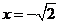 ,截
,截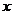 轴上的弦长为
轴上的弦长为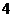 ,且过点
,且过点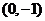 ,求函数的解析式.
,求函数的解析式.
 (04江苏)二次函数
(04江苏)二次函数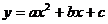 (
(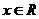 )的部分对应值如下表:
)的部分对应值如下表:
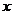 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
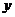 |
6 |
0 |
-4 |
-6 |
-6 |
-4 |
0 |
6 |
则不等式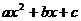
 的解集是
的解集是
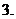 函数
函数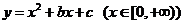 是单调函数的充要条件是
是单调函数的充要条件是
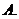
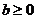
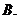
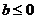
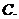
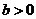
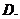
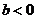
 函数
函数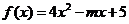 在区间
在区间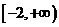 上是增函数,则
上是增函数,则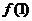 的取值范围是
的取值范围是
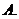
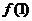 ≥
≥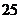
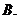
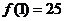
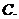
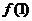 ≤
≤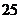
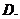
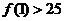
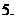 已知
已知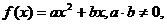 且
且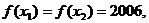
则
问题1.设二次函数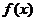 满足
满足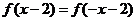 ,且图象在
,且图象在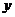 轴上的截距为
轴上的截距为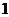 ,在
,在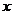 轴截得的线段长为
轴截得的线段长为 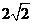 ,求
,求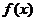 的解析式
的解析式
问题2.已知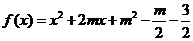 ,当
,当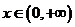 时,
时,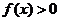 ,
,
求实数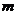 的取值范围.
的取值范围.
问题3.函数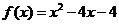 在闭区间
在闭区间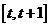 (
(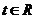 )上的最小值记为
)上的最小值记为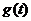 ,
,
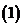 试写出
试写出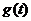 的函数表达式;
的函数表达式;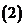 作出
作出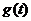 的图像并求出
的图像并求出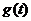 的最小值
的最小值
问题4.  方程
方程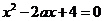 的两根均大于
的两根均大于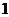 ,求实数
,求实数 的取值范围
的取值范围
 方程
方程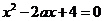 的一根大于
的一根大于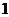 ,一根小于
,一根小于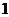 ,求实数
,求实数 的取值范围
的取值范围
 方程
方程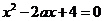 的根在
的根在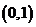 内,另一根在
内,另一根在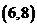 ,求实数
,求实数 的取值范围
的取值范围
问题5.已知二次函数 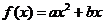 (
( 为常数,且
为常数,且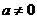 )满足条件:
)满足条件:
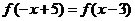 ,且方程
,且方程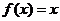 有等根.
有等根. 求
求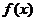 的解析式;
的解析式;
 是否存在实数
是否存在实数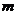 、
、 (
(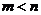 ),使
),使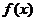 的定义域和值域分别是
的定义域和值域分别是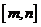 和
和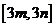 .
.
如果存在,求出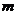 、
、 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
问题6.对于函数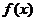 ,若存在
,若存在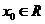 ,使
,使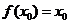 ,则称
,则称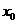 是
是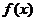 的一个
的一个
不动点,已知函数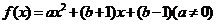 ,
,
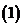 当
当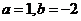 时,求函数
时,求函数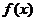 的不动点;
的不动点;
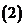 对任意实数
对任意实数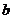 ,函数
,函数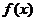 恒有两个相异的不动点,求
恒有两个相异的不动点,求 的取值范围;
的取值范围;
 问题7.已知二次函数
问题7.已知二次函数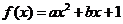 (
( 、
、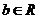 ,
,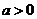 ),设方程
),设方程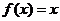 的两个实根为
的两个实根为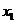 、
、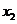 .
.
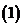 如果
如果 ,设函数
,设函数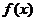 的对称轴为
的对称轴为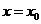 ,求证:
,求证: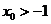 ;
;
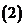 如果
如果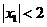 ,
,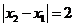 ,求
,求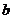 的取值范围.
的取值范围.
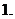 讨论二次函数
讨论二次函数 在指定区间
在指定区间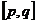 上的最值问题:
上的最值问题:
①注意对称轴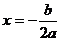 与区间
与区间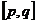 的相对位置;
的相对位置;
②函数 在区间
在区间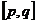 上的单调性.
上的单调性.
2.讨论二次函数的区间根的分布情况一般需从三方面考虑:①判别式; ②区间端点的函数值的符号; ③对称轴与区间的相对位置.
二次函数是高考考查的永恒主题
 二次函数的解析式的三种形式:一般式,顶点式,两根式.
二次函数的解析式的三种形式:一般式,顶点式,两根式.
 二次函数的图象及性质;
二次函数的图象及性质;
 二次函数、一元二次方程及一元二次不等式之间的关系.
二次函数、一元二次方程及一元二次不等式之间的关系.
 (高考)函数
(高考)函数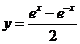 的反函数
的反函数
 是奇函数,在
是奇函数,在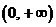 上是减函数
上是减函数  是偶函数,在
是偶函数,在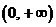 上是减函数
上是减函数
 是奇函数,在
是奇函数,在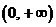 上是增函数
上是增函数  是偶函数,在
是偶函数,在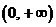 上是增函数
上是增函数
 (
(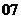 安徽)下列函数中,反函数是其自身的函数为
安徽)下列函数中,反函数是其自身的函数为


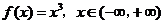

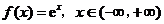

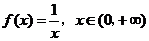
 (
( 山东)函数
山东)函数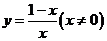 的反函数图像大致是
的反函数图像大致是
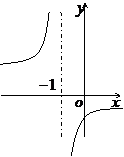
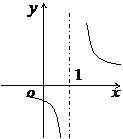
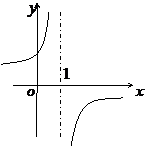
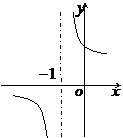




 (
( 陕西文)设函数
陕西文)设函数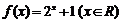 的反函数为
的反函数为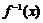 ,则函数
,则函数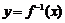 的图象是
的图象是




 (
( 湖北)已知函数
湖北)已知函数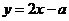 的反函数是
的反函数是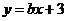 ,则
,则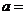 ;
;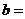
 (
( 湖北文)函数
湖北文)函数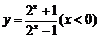 的反函数是( )
的反函数是( )

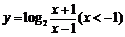

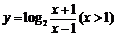

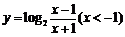

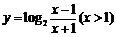
 (
( 福建文)函数
福建文)函数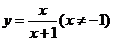 的反函数是
的反函数是

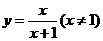

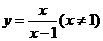

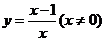

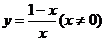
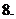 (
( 全国Ⅱ) 函数
全国Ⅱ) 函数
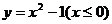 反函数是
反函数是

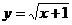
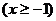

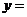 -
-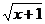
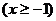

 =
=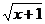
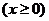

 =-
=-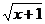
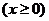
 (
( 辽宁)函数
辽宁)函数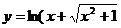 )的反函数是
)的反函数是

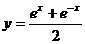

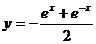

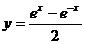

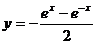
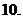 (
( 全国Ⅱ)函数
全国Ⅱ)函数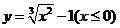 的反函数是
的反函数是

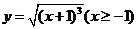



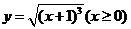

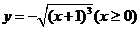
 (
( 天津)函数
天津)函数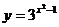 (
(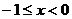 )的反函数是
)的反函数是

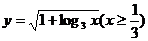

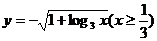

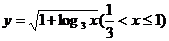

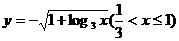
 (
( 广州模拟)已知函数
广州模拟)已知函数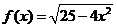 (
( ),则其反函数
),则其反函数 为
为

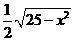
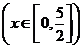

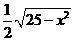
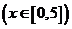

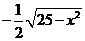
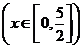

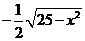
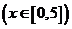
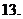 (
(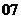 天津)函数
天津)函数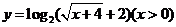 的反函数是
的反函数是

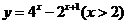

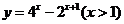

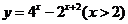

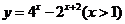
 (
( 天津文)函数
天津文)函数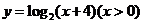 的反函数是
的反函数是

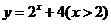

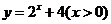

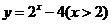

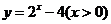
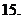 (
( 安徽文)函数
安徽文)函数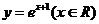 的反函数是
的反函数是

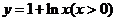

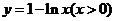

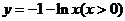

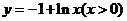
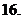 (
( 江西)设
江西)设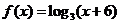 的反函数为
的反函数为 ,
,
若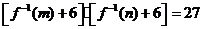 ,则
,则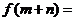
 (
( 江西文)已知函数
江西文)已知函数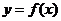 存在反函数
存在反函数 ,若函数
,若函数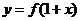 的图象
的图象
经过点 ,则函数
,则函数 的图象必经过点
的图象必经过点
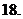 (
( 重庆)设函数
重庆)设函数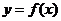 的反函数为
的反函数为 ,且
,且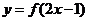 的图象过点
的图象过点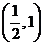 ,
,
则 的图象必过点
的图象必过点 
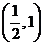

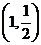

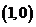

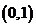
 (
( 陕西理)设函数
陕西理)设函数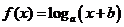
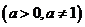 的图象过点
的图象过点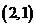 ,其反函数的图
,其反函数的图
象过点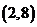 ,则
,则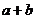 等于
等于 
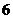

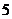


 (
( 江西模拟)已知
江西模拟)已知 ,函数
,函数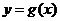 的图象与
的图象与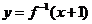 的图象关于直线
的图象关于直线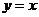 对称,则
对称,则

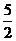

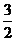



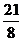
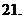 (
( 天津)已知函数
天津)已知函数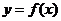 的图象与函数
的图象与函数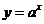 (
( 且
且 )的图象关于直线
)的图象关于直线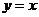 对称,记
对称,记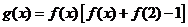 .若
.若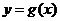 在区间
在区间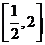 上是增函数,则实数
上是增函数,则实数 的取值范围是
的取值范围是 
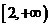

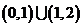

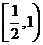


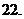 (上海高考)在
(上海高考)在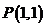 ,
,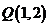 ,
,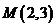 和
和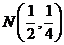 四点中,函数
四点中,函数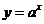 的图象与其反函数的图象的公共点只可能是
的图象与其反函数的图象的公共点只可能是



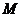

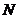
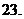 (
( 重庆文)设
重庆文)设
 为二次函数
为二次函数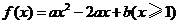 的图象与其反函数
的图象与其反函数 的图象的一个交点,则
的图象的一个交点,则

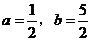

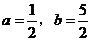

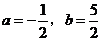

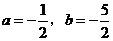
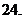 (
( 天津)设
天津)设 是函数
是函数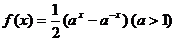 的反函数,则使
的反函数,则使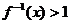
成立的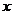 的取值范围为
的取值范围为

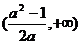

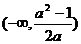

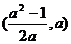

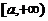
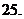 (
(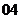 北京)函数
北京)函数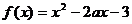 在区间
在区间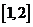 上存在反函数的充分必要条件是
上存在反函数的充分必要条件是

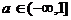

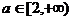

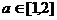

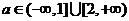
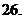 (
(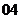 湖南)设
湖南)设 是函数
是函数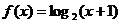 的反函数,若
的反函数,若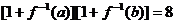 ,则
,则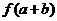 的值为
的值为
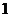




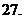 (
(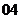 全国Ⅰ)已知函数
全国Ⅰ)已知函数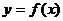 是奇函数,当
是奇函数,当 时,
时, ,设
,设 的反函数是
的反函数是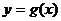 ,则
,则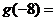

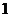

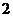

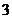

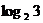
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com