
问题1. (
( 全国Ⅱ文)下面是关于三棱锥的四个命题:
全国Ⅱ文)下面是关于三棱锥的四个命题:
①底面是等边三角形,侧面与底面所成的二面角都相等的三棱锥是正三棱锥.
②底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.
③底面是等边三角形,侧面的面积都相等的三棱锥是正三棱锥.
④侧棱与底面所成的角相等,且侧面与底面所成的二面角都相等的三棱锥是正三棱锥.
其中,真命题的编号是 (写出所有真命题的编号)
 (
( 江西文)如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下
江西文)如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下 个命题中,假命题是
个命题中,假命题是
 等腰四棱锥的腰与底面所成的角都相等
等腰四棱锥的腰与底面所成的角都相等
 等腰四棱锥的侧面与底面所成的二面角都相等或互补
等腰四棱锥的侧面与底面所成的二面角都相等或互补
 等腰四棱锥的底面四边形必存在外接圆
等腰四棱锥的底面四边形必存在外接圆
 等腰四棱锥的各顶点必在同一球面上
等腰四棱锥的各顶点必在同一球面上
 (
( 全国)下面是关于四棱柱的四个命题:
全国)下面是关于四棱柱的四个命题:
① 若有两个侧面垂直于底面,则该四棱柱为直四棱柱;
② 若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱;
③ 若四个侧面两两全等,则该四棱柱为直四棱柱;
④ 若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱.
其中,真命题的编号是 (写出所有真命题的编号).
 (
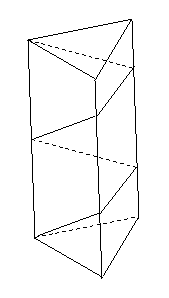
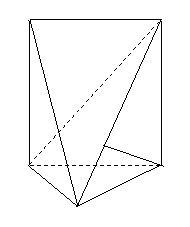
( 江西文)如右图,已知正三棱柱
江西文)如右图,已知正三棱柱
的底面边长为 ,高为
,高为 ,一质点自
,一质点自 点出发,沿着三棱柱
点出发,沿着三棱柱
的侧面绕行两周到达 点的最短路线的长为
点的最短路线的长为
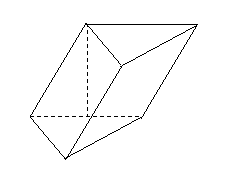 问题2.三棱柱
问题2.三棱柱 中,
中, ,
,
 、
、 、
、 的长均为
的长均为 ,点
,点 在底面
在底面
上的射影 在
在 上.
上.
 求
求 与侧面
与侧面 所成的角;
所成的角;
 若
若 点恰是
点恰是 的中点,求此三棱柱的侧面积;
的中点,求此三棱柱的侧面积;
 求此三棱柱的体积.
求此三棱柱的体积.
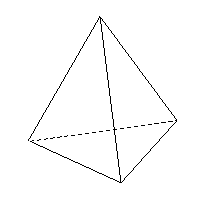 问题3.已知正四面体
问题3.已知正四面体 的棱长为
的棱长为 ,用一个
,用一个
平行于底面的平面截此四面体,所得的截面面积为 ,
,
求截面与底面之间的距离.
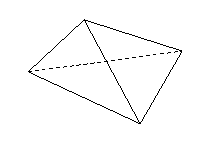 问题4.如图所示,三棱锥
问题4.如图所示,三棱锥 中,
中, ,
,
 ,
,
 ,
,
求三棱锥 的体积.(要求用四种不同的方法)
的体积.(要求用四种不同的方法)
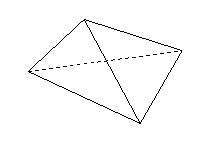
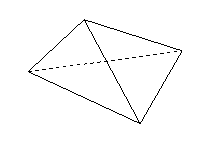

 有两个面互相平行,其余各面的公共边互相平行的多面体叫做棱柱.侧棱与底面垂直的棱柱叫做直棱柱.底面是正多边形的直棱柱叫正棱柱.
有两个面互相平行,其余各面的公共边互相平行的多面体叫做棱柱.侧棱与底面垂直的棱柱叫做直棱柱.底面是正多边形的直棱柱叫正棱柱.
 棱柱的各侧棱相等,各侧面都是平行四边形;长方体的对角线的平方等于由一个顶点出发的三条棱的平方和.
棱柱的各侧棱相等,各侧面都是平行四边形;长方体的对角线的平方等于由一个顶点出发的三条棱的平方和.
 一个面是多边形,其余各面是有一个公共顶点的三角形的多面体叫做棱锥.底面是正多边形并且顶点在底面上的射影是正多边形的中心的棱锥叫做正棱锥.
一个面是多边形,其余各面是有一个公共顶点的三角形的多面体叫做棱锥.底面是正多边形并且顶点在底面上的射影是正多边形的中心的棱锥叫做正棱锥.
 棱锥中与底面平行的截面与底面平行,并且它们面积的比等于对应高的平方比.
棱锥中与底面平行的截面与底面平行,并且它们面积的比等于对应高的平方比.
在正棱锥中,侧棱、高及侧棱在底面上的射影构成直角三角形;斜高、高及斜高在底面上的射影构成直角三角形.
 三棱锥的顶点在底面三角形上射影位置常见的有:
三棱锥的顶点在底面三角形上射影位置常见的有:
①
侧棱长相等 外心;②侧棱与底面所成的角相等
外心;②侧棱与底面所成的角相等 外心;
外心;
②
侧面与底面所成的角相等 内心;④顶点到底面三边的距离相等
内心;④顶点到底面三边的距离相等 内心;
内心;
⑤三侧棱两两垂直 垂心;⑥相对棱两两垂直
垂心;⑥相对棱两两垂直 垂心.
垂心.
 求体积常见方法有:①直接法(公式法);②转移法:利用祖暅原理或等积变化,把所求的几何体转化为与它等底、等高的几何体的体积;③分割法求和法:把所求几何体分割成基本几何体的体积;④补形法:通过补形化归为基本几何体的体积;⑤四面体体积变换法;⑥利用四面体的体积性质:(ⅰ)底面积相同的两个三棱锥体积之比等于其底面积的比;(ⅱ)高相同的两个三棱锥体积之比等于其底面积的比;(ⅲ)用平行于底面的平面去截三棱锥,截得的小三棱锥与原三棱锥的体积之比等于相似比的立方.
求体积常见方法有:①直接法(公式法);②转移法:利用祖暅原理或等积变化,把所求的几何体转化为与它等底、等高的几何体的体积;③分割法求和法:把所求几何体分割成基本几何体的体积;④补形法:通过补形化归为基本几何体的体积;⑤四面体体积变换法;⑥利用四面体的体积性质:(ⅰ)底面积相同的两个三棱锥体积之比等于其底面积的比;(ⅱ)高相同的两个三棱锥体积之比等于其底面积的比;(ⅲ)用平行于底面的平面去截三棱锥,截得的小三棱锥与原三棱锥的体积之比等于相似比的立方.
 (
( 福建)如图,直二面角
福建)如图,直二面角 中,四边形
中,四边形 是边长
是边长
 为
为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 平面
平面 .
.
 求证:
求证: 平面
平面 (略去不写);
(略去不写);
 求二面角
求二面角 的大小(略去不写);
的大小(略去不写);
 求点
求点 到平面
到平面 的距离.
的距离.

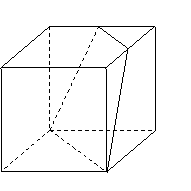 (
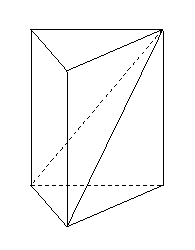
( 辽宁)如图,正方体的棱长为
辽宁)如图,正方体的棱长为 ,
, 、
、 分别是两条棱的中点,
分别是两条棱的中点,
 、
、 、
、 是顶点,那么点
是顶点,那么点 到截面
到截面 的距离是
的距离是

 (
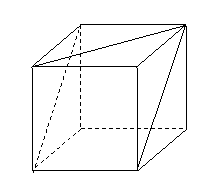
( 天津)如图,在正三棱柱
天津)如图,在正三棱柱 中,
中,
若二面角 的大小为
的大小为 ,
,
则点 到直线
到直线 的距离为
的距离为
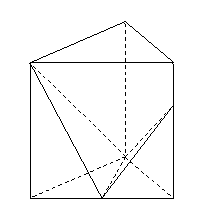
 如图,正方体
如图,正方体 的棱长为
的棱长为 ,
, 是底面
是底面
 的中心,则
的中心,则 到平面
到平面 的距离为
的距离为








 (
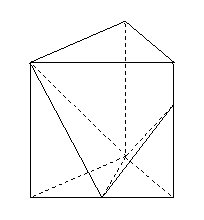
( 湖北文)如图,已知正三棱柱
湖北文)如图,已知正三棱柱 的侧棱长
的侧棱长
和底面边长均为 ,
, 是底面
是底面 边上的中点,
边上的中点, 是侧棱
是侧棱
 上的点,且
上的点,且 .
.
 求二面角
求二面角 的平面角的余弦值(略去不写);
的平面角的余弦值(略去不写);
 求点
求点 到平面
到平面 的距离(请用多种方法,至少要用向量法)
的距离(请用多种方法,至少要用向量法)

 平面
平面 ,
, 是平面
是平面 的两条斜线,
的两条斜线, 是
是 在平面
在平面 内的射影,
内的射影, ,
, ,
, ,
, ,则点
,则点 到直线
到直线 的距离为
的距离为
 在长方体
在长方体 中,
中, ,
, ,则直线
,则直线 与平面
与平面 的距离是
的距离是 








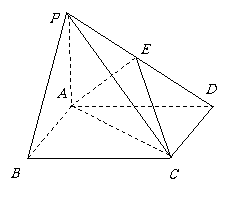 如图,在底面是矩形的四棱锥
如图,在底面是矩形的四棱锥 中,
中, 平面
平面 ,
, ,
, .
. 是
是 的中点.
的中点.
 求证:平面
求证:平面 平面
平面 (略去不写);
(略去不写);
 求二面角
求二面角 所成平面角的余弦值(略去不写);
所成平面角的余弦值(略去不写);
 求
求 点到平面
点到平面 的距离.
的距离.
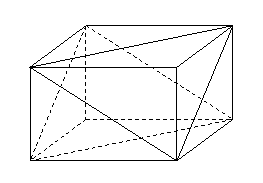
 如图,在长方体
如图,在长方体 中,
中, ,
,
 ,
, .
.
 求证:平面
求证:平面 ∥平面
∥平面 (略去不写);
(略去不写);
 求平面
求平面 与平面
与平面 间的距离.
间的距离.
问题1.( 江西)如图,在长方体
江西)如图,在长方体 中,
中, ,
, ,
,
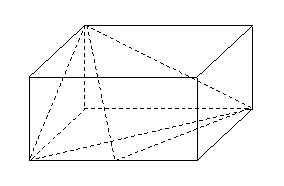 点
点 在棱
在棱 上移动.
上移动. 略;
略; 当
当 为
为 的中点时,求点
的中点时,求点 到面
到面 的距离;
的距离; 略
略
(请用多种方法,至少要用向量法)
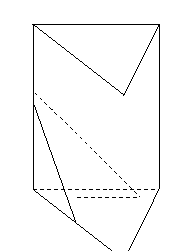 问题2.(
问题2.( 辽宁)如图,在直三棱柱
辽宁)如图,在直三棱柱 中,
中, ,
, ,
, 分别为棱
分别为棱 的中点,
的中点, 为棱
为棱 上的点,二面角
上的点,二面角 为
为 .
.
 证明:
证明: (此小题略去不写);
(此小题略去不写);
 求
求 的长,并求点
的长,并求点 到平面
到平面 的距离.
的距离.
(请用多种方法,至少要用向量法)
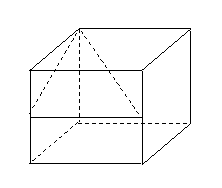 问题3.(
问题3.( 湖北文)在棱长为
湖北文)在棱长为 的正方体
的正方体 中,
中, 分别为棱
分别为棱 的中点,
的中点, 为棱
为棱 上的一点,且
上的一点,且 (
( ≤
≤ ≤
≤ ).则点
).则点 到平面
到平面 的距离为
的距离为








问题4.( 重庆)如图,在三棱柱
重庆)如图,在三棱柱 中,
中, 侧面
侧面 ,
, 为棱
为棱 上异于
上异于 、
、 的一点,
的一点, ,已知
,已知 ,
, ,
, ,
,
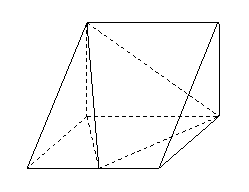
 ,求:
,求: 异面直线
异面直线 与
与 的距离;
的距离; 略.
略.
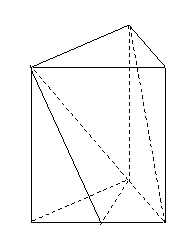
问题5.棱长均为 的正三棱柱中,
的正三棱柱中, 为
为 的中点,
的中点,
连结 ,
, ,
, .
. 求证:
求证: ∥平面
∥平面
(略去不写); 求
求 到平面
到平面 的距离.
的距离.
 七种距离:点与点、点到直线、两条平行直线、两条异面直线、点到平面、平行于平面的直线与该平面、两个平行平面之间的距离,其中点与点、点与直线、点到平面的距离是基础,求其它几种距离一般化归为求这三种距离.
七种距离:点与点、点到直线、两条平行直线、两条异面直线、点到平面、平行于平面的直线与该平面、两个平行平面之间的距离,其中点与点、点与直线、点到平面的距离是基础,求其它几种距离一般化归为求这三种距离.
 点与点的距离:
点与点的距离: 解三角形及多边形;
解三角形及多边形; 向量法:空间任意两点
向量法:空间任意两点 、
、 间的距离即线段
间的距离即线段
 的长度:设
的长度:设 、
、 ,则
,则
 两条异面直线的距离:两条异面直线的公垂线段的长度.
两条异面直线的距离:两条异面直线的公垂线段的长度.
 说明:两条异面直线的距离等于其中一条直线到过另一条直线且与这条直线平行的平面的距离
说明:两条异面直线的距离等于其中一条直线到过另一条直线且与这条直线平行的平面的距离
求法: 直接法:求两异面直线的公垂线段的长度;
直接法:求两异面直线的公垂线段的长度;
 转化法:转化为线面距离或面面距离;
转化法:转化为线面距离或面面距离; 向量法:
向量法:
法一、找平面 使
使 且
且 ∥
∥ ,则异面直线
,则异面直线 、
、 的距离
的距离
就转化为直线 到平面
到平面 的距离,又转化为点
的距离,又转化为点 到平面
到平面 的距离.
的距离.
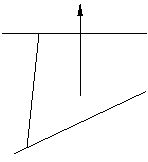 法二、在
法二、在 上取一点
上取一点 , 在
, 在 上取一点
上取一点 , 设
, 设 、
、 分别
分别
为异面直线 、
、 的方向向量,求
的方向向量,求 (
( ,
,  ),
),
则异面直线 、
、 的距离
的距离
(此方法移植于点面距离的求法).
 点到平面的距离:已知点
点到平面的距离:已知点 是平面
是平面 外的任意一点,
外的任意一点,
过点 作
作 ,垂足为
,垂足为 ,则
,则 唯一,则
唯一,则 是
是
点 到平面
到平面 的距离.即 一点到它在一个平面内的正射影
的距离.即 一点到它在一个平面内的正射影
的距离叫做这一点到这个平面的距离.
结论:连结平面 外一点
外一点 与
与 内一点所得的线段中,垂线段
内一点所得的线段中,垂线段 最短.
最短.
求法: 直接法:过点
直接法:过点 作一平面与平面
作一平面与平面 垂直,再过点
垂直,再过点 作两平面的交线的垂线即可
作两平面的交线的垂线即可
 等体积法:
等体积法: 线面平行法:若过点
线面平行法:若过点 有一直线
有一直线 ∥平面
∥平面 ,则直线
,则直线 上的任一点到平面
上的任一点到平面 的距离等于到点
的距离等于到点 到平面
到平面 的距离.
的距离. 线段比例转化法:平面的统一斜线上的两点到该平面的距离与这两点到斜足的距离成比例,运用此结论可转化为另一点到该平面的距离.
线段比例转化法:平面的统一斜线上的两点到该平面的距离与这两点到斜足的距离成比例,运用此结论可转化为另一点到该平面的距离.
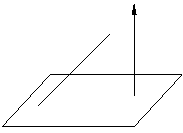
 向量法:法一、设
向量法:法一、设 是平面
是平面 的法向量,在
的法向量,在 内取一点
内取一点 ,
,
则 到
到 的距离
的距离
法二、设 于
于 ,利用
,利用 和点
和点 在
在 内的向量表示,可确定点
内的向量表示,可确定点 的位置,从而求出
的位置,从而求出 ,即直接求垂线段的长度.
,即直接求垂线段的长度.
 直线到与它平行平面的距离:一条直线上的任一点到与它平行的平面的距离,叫做这条直线到平面的距离(转化为点面距离).
直线到与它平行平面的距离:一条直线上的任一点到与它平行的平面的距离,叫做这条直线到平面的距离(转化为点面距离).
 距离的共性:这其中距离中,虽然定义不同,但总具有下列几个特征:
距离的共性:这其中距离中,虽然定义不同,但总具有下列几个特征:
 某距离是指相应线段的长度;
某距离是指相应线段的长度; 此线段是相关线段中最短的;
此线段是相关线段中最短的; 除两点间的距离外,其余总与垂直相联系,由此求距离的方法就有几何法和代数等方法.
除两点间的距离外,其余总与垂直相联系,由此求距离的方法就有几何法和代数等方法.
 求距离的一般步骤:
求距离的一般步骤: 找出或作出相关的距离;
找出或作出相关的距离; 证明它符合定义;
证明它符合定义; 归到某三角形或多边形中计算;
归到某三角形或多边形中计算; 作答.
作答.

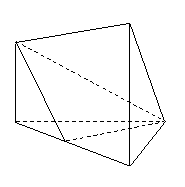 (
( 浙江)在如图所示的几何体中,
浙江)在如图所示的几何体中, 平面
平面 ,
, 平面
平面 ,
, ,且
,且 ,
, 是
是 的中点.
的中点.
 求证:
求证: ;
;
 求
求 与平面
与平面 所成的角.
所成的角.
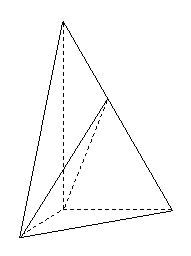
 (
( 北京)如图,在
北京)如图,在 中,
中, ,斜边
,斜边 .
.
 可以通过
可以通过 以直线
以直线 为轴旋转得到,
为轴旋转得到,
且二面角 是直二面角.动点
是直二面角.动点 的斜边
的斜边 上.
上.
 求证:平面
求证:平面 平面
平面 ;
;
 当
当 为
为 的中点时,求异面直线
的中点时,求异面直线 与
与 所成角的大小;
所成角的大小;
 求
求 与平面
与平面 所成角的最大值.
所成角的最大值.
v
 (
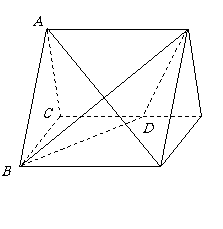
( 福建)如图,正三棱柱
福建)如图,正三棱柱 的所有棱长都为
的所有棱长都为 ,
, 为
为 中点.
中点.
 求证:
求证: 平面
平面 (此小题这里略去不做);
(此小题这里略去不做);
 求二面角
求二面角 的大小;
的大小;
 求点
求点 到平面
到平面 的距离.
的距离.
 问题1.(
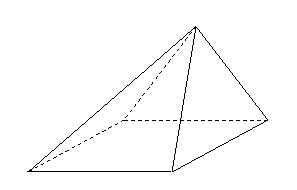
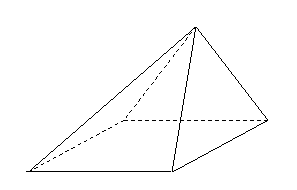
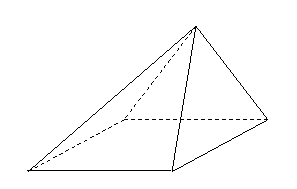
问题1.( 全国Ⅰ)四棱锥
全国Ⅰ)四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形,
侧面 底面
底面 .已知
.已知 ,
,
 ,
, ,
, .
.
 证明:
证明: ;
;
 求直线
求直线 与平面
与平面 所成角的大小.
所成角的大小.
(本小题要求用多种方法解答,包括向量法).
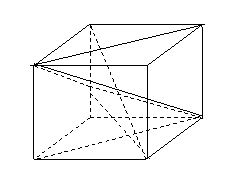 问题2. (
问题2. ( 届高三湖北、荆州、宜昌
届高三湖北、荆州、宜昌 月模拟)
月模拟)
边长为 的正方体
的正方体 中,
中, 是棱
是棱
上任一点, (
( ).
).
 若
若 时,求证:面
时,求证:面 面
面 ;
;
 试确定
试确定 值,使直线
值,使直线 与平面
与平面 所成的角
所成的角
的正切值为 .
.
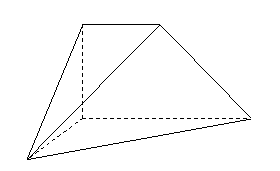 问题3.(
问题3.( 四川)如图,
四川)如图, 是直角梯形,
是直角梯形, ,
, ∥
∥ ,
,
 ,
, ,又
,又 ,
, ,
,
 ,直线
,直线 与直线
与直线 所成的角为
所成的角为 .
.
 求证:平面
求证:平面 ⊥平面
⊥平面 ;
;
 求二面角
求二面角 的大小;
的大小;
 求三棱锥
求三棱锥 的体积.
的体积.
(要求第 小题用多种方法解答,包括向量法).
小题用多种方法解答,包括向量法).
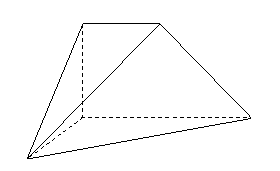
问题4.( 陕西)如图,在底面为直角梯形的四棱锥
陕西)如图,在底面为直角梯形的四棱锥 中,
中,
 ,
, ,
, 平面
平面 .
. ,
, ,
, ,
,
 求证:
求证: 平面
平面 (此小题这里略去不做);
(此小题这里略去不做); 求二面角
求二面角 的大小.
的大小.
(要求第 小题用多种方法解答,包括向量法).
小题用多种方法解答,包括向量法).
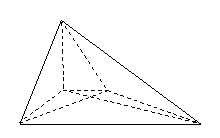



 (三)课后作业:
(三)课后作业:
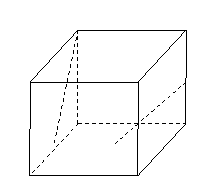
 如图所示,在棱长为
如图所示,在棱长为 的正方体
的正方体 中,
中,
 是底面
是底面 的中心,
的中心, ,
, 分别是
分别是 ,
, 的
的
中点.那么异面直线 和
和 所成角的余弦值等于
所成角的余弦值等于
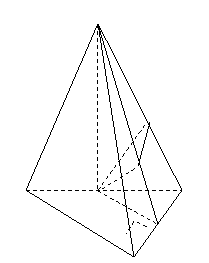
 (
( 浙江文)在三棱锥
浙江文)在三棱锥 中,
中, ,
,
点 、
、 分别是
分别是 、
、 的中点,
的中点, 底面
底面 .
.
 求证:
求证:
 平面
平面 ;
;
 求直线
求直线 与平面
与平面 所成角的大小
所成角的大小
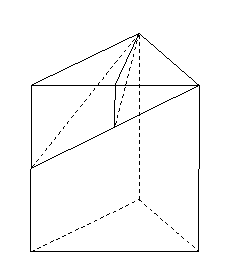
 如图,
如图, 的边长为
的边长为 ,
, ,
, ,
,
都垂直于平面 ,且
,且 ,
,
 ,点
,点 为
为 的中点,求直线
的中点,求直线
 与平面
与平面 所成的角.
所成的角.
 三垂线定理(课本
三垂线定理(课本 ):在平面内的一条直线,如果和
):在平面内的一条直线,如果和
这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.
 三垂线的逆定理(课本
三垂线的逆定理(课本 ):在平面内的一条直线,如果和
):在平面内的一条直线,如果和
这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直.
 空间角的计算步骤
空间角的计算步骤 一作、二证、三算.
一作、二证、三算.
 异面直线所成角:
异面直线所成角: 范围:
范围: ;
; 计算方法:
计算方法:
 ①平移法:一般情况下应用平行四边形的对边、梯形的平行对边、三角形的中位线进行平移.②向量法:设
①平移法:一般情况下应用平行四边形的对边、梯形的平行对边、三角形的中位线进行平移.②向量法:设 、
、 分别为异面直线
分别为异面直线 、
、 的方向向量,
的方向向量,
则两异面直线所成的角
 ;③补体法;
;③补体法;
④证明两条异面直线垂直,即所成角为 .
.
 直线与平面所成的角:①定义:(课本
直线与平面所成的角:①定义:(课本 )平面的一条斜线和它在这个平面内的射影所成的锐角,叫做这条直线和这个平面所成的角;一条直线垂直于平面,我们说它们所成的角是直角.②范围
)平面的一条斜线和它在这个平面内的射影所成的锐角,叫做这条直线和这个平面所成的角;一条直线垂直于平面,我们说它们所成的角是直角.②范围
 ;③最小角定理:斜线和平面所成的角,是这条斜线和这个平面内经过斜足的直线所成的一切角中最小的角.⑤斜线与平面所成角的计算:
;③最小角定理:斜线和平面所成的角,是这条斜线和这个平面内经过斜足的直线所成的一切角中最小的角.⑤斜线与平面所成角的计算: 直接法:关键是作垂线,找射影
直接法:关键是作垂线,找射影 可利用面面垂直的性质;
可利用面面垂直的性质;  平移法:通过三角形的中位线或平行四边形的对边平移,计算其平行线与平面所成的角.也可平移平面
平移法:通过三角形的中位线或平行四边形的对边平移,计算其平行线与平面所成的角.也可平移平面 通过等体积法求出斜线任一点到平面的距离
通过等体积法求出斜线任一点到平面的距离 ,计算这点与斜足之间的线段长
,计算这点与斜足之间的线段长 ,则
,则 .
.
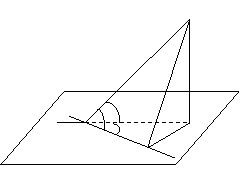
 应用结论:如右图所示,
应用结论:如右图所示, ,
, 为垂足,
为垂足, 为斜足,
为斜足,
 ,
, 与平面
与平面 所成的角为
所成的角为 ,
, ,
,
 ,则
,则 .
.
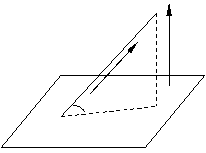
 向量法:设
向量法:设 是斜线
是斜线 的方向向量,
的方向向量, 是平面
是平面
的法向量,则斜线 与平面
与平面 所成的角
所成的角
 .
.
 二面角:①定义:平面内的一条直线把平面分为两部分,
二面角:①定义:平面内的一条直线把平面分为两部分,
其中的每一部分叫做半平面.从一条直线出发的两个半平面
所组成的图形叫做二面角,这条直线叫做二面角的棱,
 每个半平面叫做二面角的面.二面角的平面角:以二面角的棱上任一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所成的角,叫做这个二面角的平面角.规定:二面角的两个半平面重合时,二面角为
每个半平面叫做二面角的面.二面角的平面角:以二面角的棱上任一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所成的角,叫做这个二面角的平面角.规定:二面角的两个半平面重合时,二面角为 ,当两个半平面合成一个平面时,二面角为
,当两个半平面合成一个平面时,二面角为 ,因此,二面角的大小范围为
,因此,二面角的大小范围为 .②确定二面角的方法:
.②确定二面角的方法: 定义法;
定义法; 三垂线定理及其逆定理法;
三垂线定理及其逆定理法; 垂面法;
垂面法; 射影面积法:
射影面积法: ,此方法常用于无棱二面角大小的计算;无棱二面角也可以先根据线面性质恢复二面角的棱,然后再用方法
,此方法常用于无棱二面角大小的计算;无棱二面角也可以先根据线面性质恢复二面角的棱,然后再用方法 、
、 计算大小;
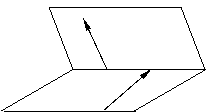
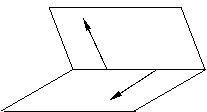
计算大小; 向量法:法一、在
向量法:法一、在 内
内
 ,在
,在 内
内
 ,其方向如左图,则二面角
,其方向如左图,则二面角 的平面角
的平面角

 ;其方向如右图,
;其方向如右图,
则二面角 的平面角
的平面角

 (同等异补)
(同等异补)
 法二、设
法二、设 ,
, 是二面角
是二面角 的两个半平面
的两个半平面
的法向量,其方向一个指向内侧,另一个指向
外侧(同等异补),则二面角 的平面角
的平面角


 (
( 陕西)如图,在底面为直角梯形的四棱锥
陕西)如图,在底面为直角梯形的四棱锥 中,
中,
 ,
, ,
, 平面
平面 .
. ,
, ,
, ,
,
 求证:
求证: 平面
平面 ;
; 略.
略.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com