解不等式：　　　　　 　

若的解集为，则不等式的解集为

已知，，若，则实数m的范围是

若有且只有一解，则实数a的值为　　　　　　　　 　

已知的解集为，则不等式

的解集为　　　 　　　　　　

已知关于的不等式≥的解集为≤或，求的范围.

若不等式对一切x恒成立,求实数的范围

若不等式对一切成立，则的范围是　　　 　　

若关于的方程有一正根和一负根，则的范围是　　　　 　

关于的方程的解为不大于的实数，则的范围为　　　　 　

不等式≥的解集为　　　　　　　

问题1．解下列不等式：

； 　　　　　　　　；　

　；　　　　　　 　

问题2.①二次不等式的解集是，则的值是

②已知不等式的解集为，则不等式

的解集为　　　　　 　　

问题3． 已知，

如果对一切，恒成立，求实数的取值范围；

如果对，恒成立，求实数的取值范围．

问题4．解关于的不等式：≥

[机动]已知二次函数的图象过点，问是否存在

常数、、，使不等式≤≤对一切都成立？

解一元二次不等式通常先将不等式化为或的形式，然后求出对应方程的根(若有根的话)，再写出不等式的解：大于时两根之外，小于时两根之间；或者利用二次函数的图象来写出一元二次不等式的解集。

分式不等式主要是转化为，再用数轴标根法求解。

高次不等式主要是利用“数轴轴标根法”解．

几点注意：①含参数的不等式要善于针对参数的取值进行讨论；

　 ②要善于运用“数形结合”法解决有关不等式问题；

　 　③要深刻理解不等式的解集与对应方程的解之间的关系，会由解集确定参数的值.

一元二次不等式的解法、一元二次方程、一元二次不等式以及二次函数之间的关系；

分式不等式的基本解法、要注意大于等于或小于等于的情况中，分母要不为零；

高次不等式的基本解法、要注重对重因式的处理．

(广东)设圆的方程为，直线的方程为的点的坐标为，那么　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　

点在直线上，但不在圆上　　 点在圆上，但不在直线上

　点既在圆上，也在直线上， 点既不在圆上，也不在直线上

(辽宁)已知点、，动点，则点的轨迹是　　 圆　　 椭圆　 双曲线　 　抛物线

方程表的图形是　 两个点四个点两条直线四条直线

设曲线是到两坐标轴距离相等点的轨迹，那么的方程是

和

已知点，内接于圆，且，当在圆上运动时，中点的轨迹方程是

若两直线与交点在曲线上，则　　　　

若曲线通过点，则的取值范围是　　　　 　　

画出方程所表示的图形：

为定点，线段在定直线上滑动，已知，到的距离为，求的外心的轨迹方程.

设，求两直线：与：的交点的轨迹方程

问题1．(武汉调研)如果命题“坐标满足方程的点都在曲线上”

是不正确的，那么下列命题正确的是 坐标满足方程的点都不在曲线上；

曲线上的点不都满足方程；坐标满足方程的点有些在曲线上，有些不在曲线上；至少有一个点不在曲线上，其坐标满足方程.

如果曲线上的点满足方程，则以下说法正确的是：

曲线的方程是；方程的曲线是；

坐标满足方程的点在曲线上；

坐标不满足方程的点不在曲线上；

判断下列结论的正误，并说明理由：

①　　 过点且垂直于轴的直线的方程为；

②到轴距离为的点的直线的方程为；

③到两坐标轴的距离乘积等于的点的轨迹方程为；

④的顶点，，，为的中点，则中线的方程为.

作出方程所表示的曲线.

问题2．设动直线垂直于轴，且与椭圆交于两点，是上满足的点，求点的轨迹方程.

问题3．已知中，、、所对的边分别为，且

成等差数列，，求顶点的轨迹方程.

问题4．若动点在上移动，求与连线中点的轨迹方程

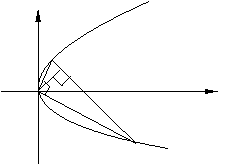问题5．已知抛物线，为顶点，

为抛物线上的两动点，且，如果

于，求点的轨迹方程.

掌握“方程与曲线”的充要关系；

求轨迹方程的常用方法：轨迹法、定义法、代入法、参数法、待定系数法、直接法和交轨法、向量法. 要注意“查漏补缺，剔除多余”.

曲线的方程与方程的曲线的概念；用直接法求曲线的方程的方法和步骤。