
问题1.已知两条直线 :
: 和
和 :
: ,求满足下列条件的
,求满足下列条件的 值:
值:
 ,且过点
,且过点

 ,且坐标原点到这两条直线的距离相等.
,且坐标原点到这两条直线的距离相等.
问题2.等腰三角形一腰所在的直线 的方程是
的方程是 ,底边所在的直线
,底边所在的直线 的方程是
的方程是 ,点
,点 在另一腰上,求这腰所在直线
在另一腰上,求这腰所在直线 的方程.
的方程.
问题3.已知三条直线 :
:
 。直线
。直线 :
: 和直线
和直线
 :
: ,且
,且 与
与 的距离是
的距离是 .
.  求
求 的值;
的值;  求
求 到
到 的角
的角 ;
;
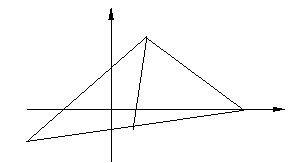 问题4.如图所示,
问题4.如图所示, 的顶点
的顶点 ,
, ,
,
 ,求
,求 的平分线
的平分线 所在直线的方程.
所在直线的方程.
(至少用两种解法)
(1)平面内两条直线的位置关系有三种:重合、平行、相交.
 当直线不平行于坐标轴时,直线与圆的位置关系可根据下表判定
当直线不平行于坐标轴时,直线与圆的位置关系可根据下表判定
|
|
斜截式 |
一般式 |
|
方 程 |
 : :  : : |
 : :  : : |
|
相 交 |
 |
 |
|
垂 直 |
 |
 |
|
平 行 |
 且 且 |
 或 或 |
|
重 合 |
 且 且 |
  |
 当直线平行于坐标轴时可结合图形进行考虑其位置关系.
当直线平行于坐标轴时可结合图形进行考虑其位置关系.
说明:由于直线 的方向向量为
的方向向量为 ,可推导上述结论.
,可推导上述结论.
(2)点到直线的距离、直线与直线的距离:
 点
点 到直线
到直线 的距离为:
的距离为:

 直线
直线 ,且其方程分别为
,且其方程分别为 :
: ,
, :
:
则 与
与 的距离为:
的距离为:

(3)两条直线的夹角公式:若直线 的斜率为
的斜率为 ,
, 的斜率为
的斜率为 ,则:
,则:
 直线
直线 到
到 的角满足:tan
的角满足:tan .
.
 直线
直线 与直线
与直线 所成的角(简称夹角)
所成的角(简称夹角) 满足:
满足:
说明:①当 和
和 的斜率都不存在时,所成的角为
的斜率都不存在时,所成的角为 ;②当
;②当 与
与 的斜率有一个存在时,可画图、观察,根据另一条直线的斜率得出所求的角;③
的斜率有一个存在时,可画图、观察,根据另一条直线的斜率得出所求的角;③  到
到 的角
的角 不同于
不同于 到
到 的角
的角 ,它们满足:
,它们满足: .④到角范围:
.④到角范围: ;夹角范围:
;夹角范围:
(4)两条直线的交点:两条直线的交点的个数取决于这两条直线的方程组成的方程组的解的个数.
 (
( 全国)直线
全国)直线
 的倾斜角为
的倾斜角为








 (
( 湖南文)设直线
湖南文)设直线 的倾斜角为
的倾斜角为 ,且
,且 ,则
,则
满足: 







 (
( 北京)若三点
北京)若三点
 共线,则
共线,则 的值等于
的值等于
 (
( 湖南)设直线的方程是
湖南)设直线的方程是 ,从
,从 这五个数中每次取两个不同的数
这五个数中每次取两个不同的数
作为 的值,则所得不同直线的条数是
的值,则所得不同直线的条数是 







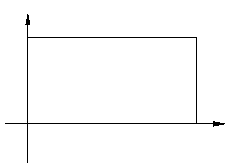
 (
( 广东)在平面直角坐标系中,已知矩形
广东)在平面直角坐标系中,已知矩形 的长
的长
为 ,宽为
,宽为 ,
, 、
、 边分别在
边分别在 轴、
轴、 轴的正半轴上,
轴的正半轴上,
 点与坐标原点重合(如图所示).将矩形折叠,使
点与坐标原点重合(如图所示).将矩形折叠,使 点
点
落在线段 上.(Ⅰ)若折痕所在直线的斜率为
上.(Ⅰ)若折痕所在直线的斜率为 ,
,
试写出折痕所在直线的方程;(Ⅱ)求折痕的长的最大值.
 (
( 上海春)若直线
上海春)若直线 的倾斜角为
的倾斜角为 ,则
,则
 等于
等于
 等于
等于
 等于
等于
 不存在
不存在
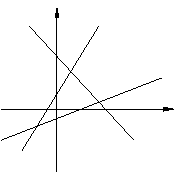
 (
( 全国)如右图,直线
全国)如右图,直线 的斜率分别为
的斜率分别为 ,则
,则








 (
( 合肥模拟)直线
合肥模拟)直线 的方向向量为
的方向向量为 ,直线
,直线 的倾斜角为
的倾斜角为
 ,则
,则








 (
( 西安理工附中高二数学)直线
西安理工附中高二数学)直线 的方向向量为
的方向向量为 ,则
,则 的倾斜角为
的倾斜角为









 ,则直线
,则直线 的倾斜角为
的倾斜角为








 直线
直线
 的倾斜角范围是
的倾斜角范围是








 (
( 上海)下面命题中正确的是:
上海)下面命题中正确的是:
 经过定点
经过定点 的直线都可以用方程
的直线都可以用方程 表示.
表示.
 经过任意两个不同的点
经过任意两个不同的点 ,
, 的直线都可以用方程
的直线都可以用方程
 表示;
表示; 不经过原点的直线都可以用方程
不经过原点的直线都可以用方程 表示
表示
 经过点
经过点 的直线都可以用方程
的直线都可以用方程 表示
表示
 已知三点
已知三点 、
、 、
、 共线,则
共线,则 的取值是
的取值是







 过点
过点 在两条坐标轴上的截距绝对值相等的直线条数有
在两条坐标轴上的截距绝对值相等的直线条数有







 直线
直线 的倾斜角为
的倾斜角为
 (
( 上海春)若直线
上海春)若直线 的倾斜角为
的倾斜角为 ,且过点
,且过点 ,则直线
,则直线 的方程为
的方程为
 一直线过点
一直线过点 ,且在两轴上的截距之和为
,且在两轴上的截距之和为 ,则此直线方程是
,则此直线方程是
 若两点
若两点 ,
, ,直线
,直线 的倾斜角是直线
的倾斜角是直线 的一半,求直线
的一半,求直线 的斜率
的斜率
 已知
已知 ,
, 两点,直线
两点,直线 的斜率为
的斜率为 ,若一直线
,若一直线 过线段
过线段 的中点且倾斜角的正弦值为
的中点且倾斜角的正弦值为 ,求直线
,求直线 的方程.
的方程.
问题1. 已知两点 ,
, .
. 求直线
求直线 的斜率
的斜率 和倾斜角
和倾斜角 ;
;
 求直线
求直线 的方程;
的方程; 若实数
若实数 ,求
,求 的倾斜角
的倾斜角 的范围.
的范围.
问题2. (
( 河南)已知直线
河南)已知直线 过点
过点 且与以点
且与以点 ,
, 为
为
端点的线段相交,求直线 的斜率及倾斜角
的斜率及倾斜角 的范围.
的范围. 求函数
求函数 的值域.
的值域.
问题3.求满足下列条件的直线 的方程:
的方程:
 过两点
过两点 ,
, ;
; 过
过 ,且以
,且以 为方向向量;
为方向向量;
 过
过 ,倾斜角是直线
,倾斜角是直线 的倾斜角的
的倾斜角的 倍;
倍;
 过
过 ,且在
,且在 轴,
轴, 轴上截距相等;
轴上截距相等;
 在
在 轴上的截距为
轴上的截距为 ,且它与两坐标轴围成的三角形面积为
,且它与两坐标轴围成的三角形面积为 ;
;
 过
过 ,且与
,且与 轴、
轴、 轴分别交于
轴分别交于 、
、 两点,若点
两点,若点 分
分 比为
比为 .
.
问题4. (
( 上海春)直线
上海春)直线 过点
过点 ,且分别与
,且分别与 轴的正半轴于
轴的正半轴于 两点,
两点, 为原点. 求
为原点. 求 面积最小值时
面积最小值时 的方程,
的方程,
 取最小值时
取最小值时 的方程.
的方程.
 倾斜角:一条直线
倾斜角:一条直线 向上的方向与
向上的方向与 轴的正方向所成的最小正角,叫做直线的倾斜角,范围为
轴的正方向所成的最小正角,叫做直线的倾斜角,范围为 .
.
斜率:当直线的倾斜角不是 时,则称其正切值为该直线的斜率,即
时,则称其正切值为该直线的斜率,即 ;当直线的倾斜角等于
;当直线的倾斜角等于 时,直线的斜率不存在。
时,直线的斜率不存在。
 过两点
过两点 ,
,
 的直线的斜率公式:
的直线的斜率公式:
若 ,则直线
,则直线 的斜率不存在,此时直线的倾斜角为
的斜率不存在,此时直线的倾斜角为 .
.
 (课本
(课本 )直线的方向向量:设
)直线的方向向量:设 为直线上的两点,则向量
为直线上的两点,则向量 及与它平行的向量都
及与它平行的向量都
称为直线的方向向量.若 ,
, ,则直线的方向向量为
,则直线的方向向量为 =
= .
.
直线 的方向向量为
的方向向量为 .当
.当 时,
时, 也为直线的一个方向向量.
也为直线的一个方向向量.
 直线方程的种形式:
直线方程的种形式:
|
名称 |
方程 |
适用范围 |
|
斜截式 |
 |
不含垂直于 轴的直线 轴的直线 |
|
点斜式 |
 |
不含直线 |
|
两点式 |
 |
不含直线 ( ( )和 )和直线   |
|
截距式 |
 |
不含垂直于坐标轴和过原点的直线 |
|
一般式 |
  |
平面直角坐标系内的直线都适用 |
 (
( 重庆) 设数列
重庆) 设数列 满足
满足 ,
, ,(
,( ,…).
,…).
 证明
证明 对一切正整数
对一切正整数 成立;
成立;
 令
令 ,判断
,判断 的大小,并说明理由 .
的大小,并说明理由 .
 (
( 全国)已知数列
全国)已知数列 的前
的前 项和
项和 满足
满足 ,
, ≥
≥ .
.
 写出数列
写出数列 的前三项
的前三项 ,
, ,
, ;
;
 求数列
求数列 的通项公式;
的通项公式;
 证明:对任意的整数
证明:对任意的整数 ,有
,有 .
.
 (
( 江苏)设数列
江苏)设数列 的前
的前 项和为
项和为 ,已知
,已知 ,且
,且
 ,
, 其中
其中 为常数.
为常数.
(Ⅰ)求 与
与 的值;(Ⅱ)证明:数列
的值;(Ⅱ)证明:数列 为等差数列;
为等差数列;
(Ⅲ)证明:不等式 对任何正整数
对任何正整数 都成立.
都成立.
 数列
数列 的通项公式是
的通项公式是 ,数列
,数列 中最大的项是
中最大的项是
 第
第 项
项  第
第 项
项  第
第 项和第
项和第 项
项  第
第 项和第
项和第 项
项
 已知
已知 ,且满足
,且满足 ,则
,则 的最小值为
的最小值为








 若实数
若实数 满足
满足
 ,则
,则 的最大值是
的最大值是








 设
设 ,
, ,
, ,则
,则 的取值范围是
的取值范围是








 已知
已知 是大于
是大于 的常数,则当
的常数,则当 时,函数
时,函数 的最小值为
的最小值为
 设
设 ,且
,且 ,
, ,求
,求 的范围
的范围
 函数
函数 在
在 有意义,求
有意义,求 的取值范围
的取值范围
 周长为
周长为 的直角三角形面积的最大值为
.
的直角三角形面积的最大值为
.
 设
设 ,
, 且
且 恒成立,则
恒成立,则 的最大值为
的最大值为
 (
( 届高三桐庐中学月考)若直线
届高三桐庐中学月考)若直线 始终平分圆
始终平分圆 的周长,则
的周长,则 的最小值为
的最小值为 







 若不等式
若不等式 的解集为
的解集为 ,求正实数
,求正实数 的取值范围.
的取值范围.
 (
( 苏大附中模拟)对于任意的
苏大附中模拟)对于任意的 ,不等式
,不等式 恒成立,则实数
恒成立,则实数
 的取值范围是
的取值范围是
 若对一切实数
若对一切实数 ,不等式
,不等式 ≥
≥ 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.

 为何实数时,方程
为何实数时,方程 的两根都大于
的两根都大于
 光线每通过一块玻璃板,其强度要减少
光线每通过一块玻璃板,其强度要减少 ,把几块这样的玻璃板重叠起来,能使通过它们的光线强度在原强度的
,把几块这样的玻璃板重叠起来,能使通过它们的光线强度在原强度的 以下.
以下.
 已知函数
已知函数 .
. 求证:函数
求证:函数 在
在 上是增函数
上是增函数
 若
若 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
 若函数
若函数 在
在 上的值域是
上的值域是
 ,求实数
,求实数 的取值范围.
的取值范围.
 (
( 届高三桐庐中学月考)已知
届高三桐庐中学月考)已知
 若
若 ,求方程
,求方程 的解;
的解; 若关于
若关于 的方程
的方程 在
在 上有两个解
上有两个解 ,求
,求 的取值范围,并证明
的取值范围,并证明
 (
( 届高三黄冈中学)已知关于
届高三黄冈中学)已知关于 的不等式
的不等式 的解集为空集,求实数
的解集为空集,求实数 的值或取值范围
的值或取值范围

 对于函数
对于函数 ,当
,当 ≤
≤ 时,有
时,有 ≤
≤ .
.
 求证:
求证: ≤
≤ ,
, ≤
≤ ;
; 求证:
求证: ≤
≤ ;
; 求证:
求证: ≤
≤
问题1. 设关于 的不等式
的不等式 和
和 的解集依次为
的解集依次为 、
、 求使
求使 的实数
的实数 的取值范围.
的取值范围.
问题2.已知函数 在
在 上为减函数,求实数
上为减函数,求实数 的取值范围.
的取值范围.
问题3. 若关于
若关于 的方程
的方程 有实数解,求实数
有实数解,求实数 的取值范围.
的取值范围.
 解关于
解关于 的不等式:
的不等式: (
( ).
).
问题4.已知正项数列 中,对于一切
中,对于一切 均有
均有 ≤
≤ 成立.
成立.
 求证:数列
求证:数列 中的任何一项都小于
中的任何一项都小于 ;
; 探究
探究 与
与 的大小,并加以证明.
的大小,并加以证明.
问题5.( 北京春)经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量
北京春)经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量 (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度 (千米/小时)之间的函数关系为:
(千米/小时)之间的函数关系为:
 .
. 在该时段内,当汽车的平均速度
在该时段内,当汽车的平均速度 为多少时,车流量最大?最大车流量为多少?(精确到
为多少时,车流量最大?最大车流量为多少?(精确到 千辆/小时)
千辆/小时) 若要求在该时段内车流量超过
若要求在该时段内车流量超过 千辆/小时,则汽车站的平均速度应在什么范围内?
千辆/小时,则汽车站的平均速度应在什么范围内?
 (
( 安徽)若对任意
安徽)若对任意 ,不等式
,不等式 ≥
≥ 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是



 ≤
≤

 <
<

 ≥
≥
 (
( 北京)在下列四个函数中,满足性质:“对于区间
北京)在下列四个函数中,满足性质:“对于区间 上的任意
上的任意 ,
,
 恒成立”的只有
恒成立”的只有








 (
( 上海)三个同学对问题“关于
上海)三个同学对问题“关于 的不等式
的不等式 ≥
≥ 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围”提出各自的解题思路.
的取值范围”提出各自的解题思路.
甲说:“只须不等式左边的最小值不小于右边的最大值”.
乙说:“把不等式变形为左边含变量 的函数,右边仅含常数,求函数的最值”.
的函数,右边仅含常数,求函数的最值”.
丙说:“把不等式两边看成关于 的函数,作出函数图像”.
的函数,作出函数图像”.
参考上述解题思路,你认为他们所讨论的问题的正确结论,即 的取值范围是
的取值范围是
 (
( 重庆)设
重庆)设 ,函数
,函数 有最大值,则不等式
有最大值,则不等式 的解集为
的解集为
 (
( 海南)设函数
海南)设函数 .
.
 解不等式
解不等式 ;
; 求函数
求函数 的最小值.
的最小值.
 (
( 北京文)记关于
北京文)记关于 的不等式
的不等式 的解集为
的解集为 ,不等式
,不等式 ≤
≤ 的解集为
的解集为 .
.
 若
若 ,求
,求 ;
; 若
若 ,求正数
,求正数 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com