
 求下列函数的值域:
求下列函数的值域:
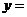
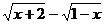 (
(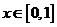 );
);
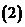
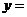
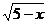 +
+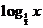 ;
;
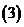

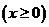 ;
;
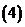
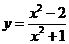 ;
;
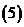

 函数
函数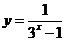 的值域是
的值域是
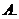
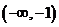
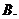
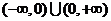
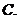
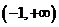
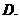

 已知函数
已知函数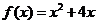 ,则
,则 的值域是
的值域是
 函数
函数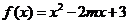 在区间
在区间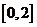 上的值域为
上的值域为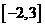 ,则
,则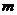 的值为( )
的值为( )
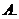
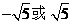
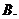
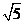 或
或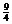
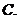
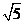
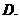
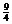
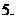 (
(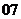 江苏通州一中质检)函数
江苏通州一中质检)函数 的最小值为
的最小值为
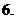 (
(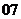 江苏)已知函数
江苏)已知函数 在区间
在区间 上的最大值与最小值分别为
上的最大值与最小值分别为
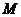 、
、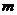 ,则
,则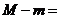 _____.
_____.
 若函数
若函数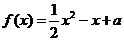 的定义域和值域均为
的定义域和值域均为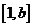
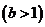 ,求
,求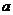 、
、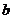 的值
的值
 函数
函数
 的最小值是( )
的最小值是( )
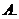
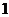
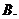
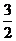
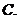
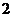
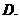
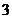
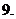 (
(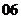 长春四市一模)函数
长春四市一模)函数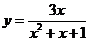
 的值域是
的值域是
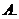
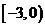
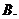
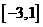
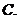
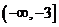
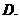
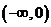
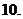 (
( 新海中学模拟)函数
新海中学模拟)函数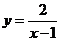 的定义域是
的定义域是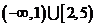 ,则其值域是
,则其值域是
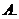
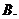
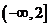
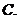

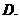
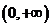
 求函数
求函数
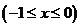 的值域
的值域
 定义在
定义在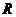 上的函数
上的函数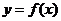 的值域为
的值域为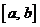 ,则函数
,则函数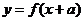 的值域为
的值域为
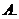

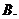
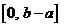
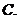
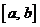
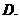

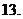 已知
已知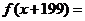

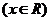 ,那么函数
,那么函数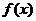 的最小值为
的最小值为
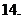 若
若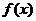 的值域为
的值域为 ,则
,则 的值域为
的值域为
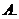
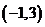
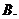

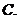
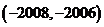
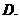 以上都不对
以上都不对
 (
( 江西)设函数
江西)设函数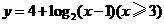 ,则其反函数的定义域为
,则其反函数的定义域为
 已知函数
已知函数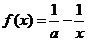
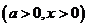 .
.
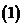 若
若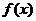 在
在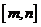 上的值域是
上的值域是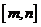 ,求
,求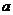 的取值范围,并求相应的
的取值范围,并求相应的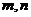 的值;
的值;
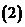 若
若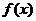 ≤
≤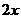 在
在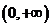 上恒成立,求
上恒成立,求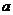 的取值范围
的取值范围
 函数
函数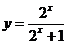 的值域为
的值域为
 若函数
若函数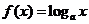 在
在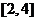 上的最大值与最小值之差为
上的最大值与最小值之差为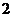 ,则
,则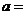
 已知
已知 (
(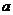 是常数),在
是常数),在 上有最大值
上有最大值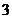 ,那么在
,那么在 上的最小值是
上的最小值是 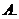
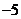
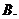
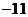
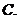
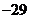
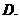
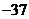
问题1.求下列函数的值域:
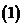
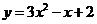 ;
; 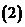
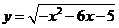 ;
;
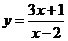 ;
;
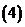
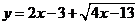 ;
;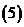
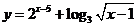
 ;
;
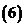
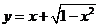 ;
;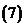
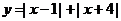 ;
;
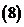
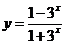 ;
;
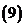
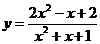 ;
;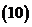
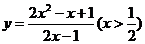 ;
;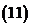
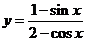 ;
;
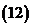
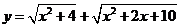 ;
;
问题2.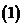 求函数
求函数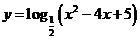 的值域;
的值域;
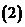 已知
已知 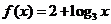 ,
,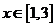 ,求函数
,求函数 的值域;
的值域;
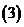 若函数
若函数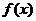 的值域为
的值域为 ,求
,求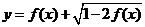 的值域.
的值域.
问题3.已知函数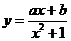 的值域为
的值域为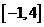 ,求常数
,求常数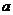 、
、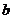 的值
的值
求函数的值域的方法常用的有:直接法,分离常数法,换元法,配方法,判别式法,不等式法,利用某些函数的有界性法,数形结合法,函数的单调性法,利用导数法,利用平移等.
 函数的值域的定义;
函数的值域的定义; 确定函数的值域的原则:定义域优先原则
确定函数的值域的原则:定义域优先原则
 求函数的值域的方法.
求函数的值域的方法.
 (
( 春安徽理)若
春安徽理)若 ,则
,则 =
=

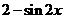


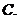


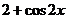
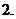 (
( 湖北理)已知
湖北理)已知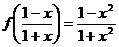 ,则
,则 的解析式可取为 ( )
的解析式可取为 ( )



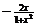
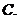


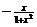
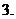 (
( 江苏)已知
江苏)已知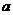 、
、 为常数,若
为常数,若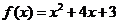 ,
,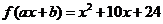 ,
,
则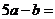
 (
( 全国Ⅰ文)已知二次函数
全国Ⅰ文)已知二次函数 的二次项系数为
的二次项系数为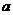 ,且不等式
,且不等式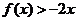 的解集
的解集
为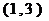 (Ⅰ)若方程
(Ⅰ)若方程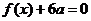 有两个相等的根,求
有两个相等的根,求 的解析式;
的解析式;
(Ⅱ)若 的最大值为正数,求
的最大值为正数,求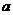 的取值范围
的取值范围
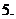 (
( 湖北)函数
湖北)函数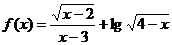 的定义域是
的定义域是
 (
( 陕西文)函数
陕西文)函数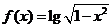 的定义域为( )
的定义域为( )

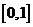

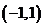
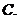


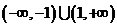
 (
( 湖北文)设
湖北文)设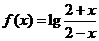 ,则
,则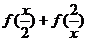 的定义域为( )
的定义域为( )

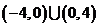

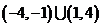
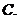


 (
(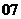 江西文)函数
江西文)函数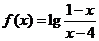 的定义域为( )
的定义域为( )

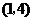

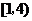
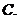
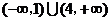


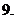 (
(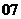 上海)函数
上海)函数 的定义域为
的定义域为
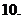 (
( 江西)函数
江西)函数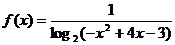 的定义域为( )
的定义域为( )






 (
( 陕西理)设函数
陕西理)设函数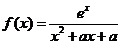 ,其中
,其中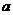 为实数.
为实数.
(Ⅰ)若 的定义域为
的定义域为 ,求
,求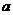 的取值范围;
的取值范围;
(Ⅱ)当 的定义域为
的定义域为 时,求
时,求 的单调减区间.
的单调减区间.
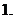 下列各函数解析式中,满足
下列各函数解析式中,满足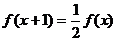 的是
的是



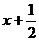
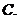
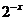

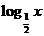
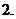 已知
已知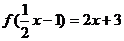 ,且
,且 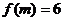 ,则
,则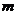 等于
等于



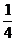
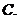
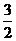


 已知
已知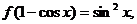 求
求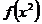 的解析式。
的解析式。
 已知
已知 对于定义域内的任何
对于定义域内的任何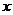 、
、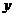 都有关系式:
都有关系式: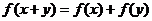 成立,
成立,
那么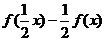
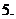 若
若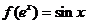 ,则
,则
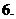 若函数
若函数 满足关系式
满足关系式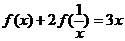 ,则
,则 的表达式为__________.
的表达式为__________.
 设函数
设函数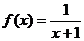 的图象为
的图象为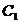 ,若函数
,若函数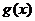 的图象
的图象 与
与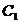 关于
关于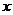 轴对称,
轴对称,
则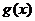 的解析式为
的解析式为
 求定义域: ①
求定义域: ①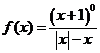 ②
②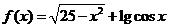
③ ④
④ 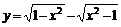
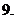 已知
已知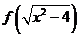 的定义域为
的定义域为 ,求
,求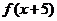 的定义域
的定义域
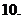 已知函数
已知函数
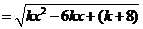 的定义域为
的定义域为 ,求实数
,求实数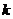 的范围
的范围
 周长为
周长为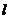 的铁丝弯成下部为矩形,上部分为半圆形的框架,,若矩形底边长为
的铁丝弯成下部为矩形,上部分为半圆形的框架,,若矩形底边长为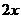 ,
,
求此框架围成面积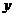 与
与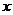 的函数关系式,并求定义域
的函数关系式,并求定义域
 函数
函数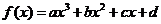 的部分数值如下表:
的部分数值如下表:
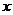


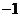
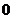
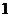
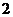


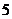
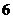
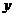
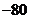
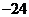
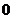

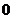
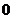
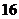
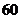
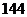
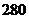
则函数 的定义域为
的定义域为
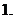 已知
已知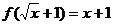 ,则函数
,则函数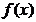 的解析式为
的解析式为




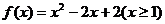

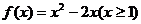
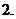 已知
已知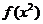 的定义域为
的定义域为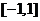 ,则
,则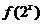 的定义域为
的定义域为
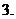 函数
函数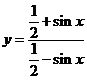 的定义域为
的定义域为
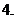 设二次函数
设二次函数 的最小值为
的最小值为 ,且
,且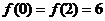 ,求
,求 的解析式
的解析式
问题1.已知函数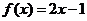 ,
,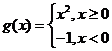 ,求
,求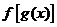 和
和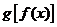 的解析式
的解析式
问题2.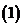 已知
已知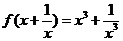 ,求
,求 ;
;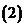 已知
已知 ,求
,求 ;
;
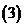 已知
已知 是一次函数,且满足
是一次函数,且满足 ,求
,求 ;
;
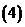 已知
已知 满足
满足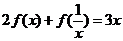 ,求
,求 ;
;
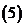 函数
函数 对一切实数
对一切实数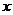 、
、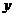 均有
均有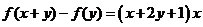 成立,且
成立,且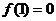 ,
,
①求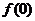 ;②求
;②求
问题3. 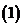 (
(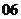 广东)函数
广东)函数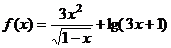 的定义域是
的定义域是

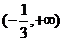

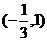
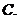
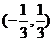

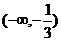
 已知函数
已知函数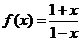 的定义域为
的定义域为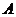 ,函数
,函数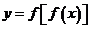 的定义域为
的定义域为 ,
,
则 
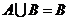

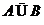
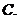


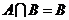
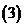 若函数
若函数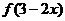 的定义域为
的定义域为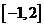 ,则函数
,则函数 的定义域是
的定义域是

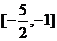

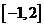
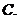
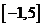

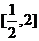
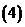 已知函数
已知函数 的定义域为
的定义域为 ,则
,则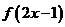 的定义域是
的定义域是

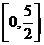

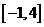
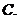
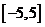

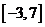
 求函数解析式的题型有:
求函数解析式的题型有:
 已知函数类型,求函数的解析式时常用待定系数法;
已知函数类型,求函数的解析式时常用待定系数法;
 已知
已知 求
求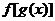 或已知
或已知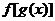 求
求 :换元法、配凑法;
:换元法、配凑法;
 应用题求函数解析式常要根据实际问题的意义来布列函数关系,确定函数的定义域.
应用题求函数解析式常要根据实际问题的意义来布列函数关系,确定函数的定义域.
 求函数定义域一般有三类问题:
求函数定义域一般有三类问题:
 给出函数解析式的:函数的定义域是使解析式有意义的自变量的取值集合;
给出函数解析式的:函数的定义域是使解析式有意义的自变量的取值集合;
 实际问题:函数的定义域的求解除要考虑解析式有意义外,还应考虑使实际问题有意义;
实际问题:函数的定义域的求解除要考虑解析式有意义外,还应考虑使实际问题有意义;
 已知
已知 的定义域求
的定义域求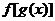 的定义域或已知
的定义域或已知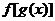 的定义域求
的定义域求 的定义域:
的定义域:
①若已知 的定义域
的定义域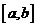 ,其复合函数
,其复合函数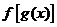 的定义域应由
的定义域应由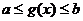 解出;
解出;
②若复合函数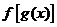 的定义域为
的定义域为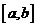 ,则
,则 的定义域为
的定义域为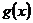 在
在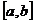 上的值域.
上的值域.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com