
2.“中州”是我国的古都聚集地,在这里曾发生过武王伐纣、陈桥兵变等历史事件。“中州”的地理位置应相当于今天的 ( )
A.河南 B.陕西 C.甘肃 D.山东
1.著名史学家苏秉琦先生指出,中国农业起源具有“满天星斗”的特点,以下选项中,最能印证该观点的是 ( )
A.北京人遗址已发现采集和猎取食物的遗迹
B.湖南玉蟾岩,陕西半坡遗址、浙江河渡遗址等地都发现了人工栽培水稻的遗存
C.除了黍、粟、水稻外,起源于战国的粮食作物还有稷、大豆等
D.在浙江余姚河姆渡的考古发掘中,发现存在的大量稻谷的遗存
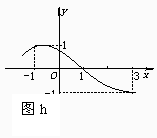
11.函数y=Asin(ωx+φ)?(|φ|?<π)的图象如图h,求函数的表达式
选题意图:考查数形结合的思想方法
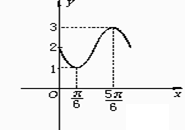
1 如图a是周期为2π的三角函数y=f(x)的图象,那么f(x)可以写成( )
如图a是周期为2π的三角函数y=f(x)的图象,那么f(x)可以写成( )
A sin(1+x)
sin(1+x)
B sin(-1-x)
sin(-1-x)
 C
C sin(x-1)
sin(x-1)
D sin(1-x)
sin(1-x)
2 如图b是函数y=Asin(ωx+φ)+2的图象的一部分,它的振幅、周期、初相各是( )
如图b是函数y=Asin(ωx+φ)+2的图象的一部分,它的振幅、周期、初相各是( )
A A=3,T=
A=3,T=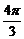 ,φ=-
,φ=-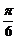
 B
B A=1,T=
A=1,T=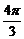 ,φ=-
,φ=-
C A=1,T=
A=1,T=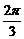 ,φ=-
,φ=-
 D
D A=1,T=
A=1,T=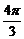 ,φ=-
,φ=-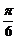
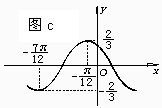
3 如图c是函数y=Asin(ωx+φ)的图象的一段,它的解析式为( )
如图c是函数y=Asin(ωx+φ)的图象的一段,它的解析式为( )
A
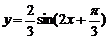 B
B
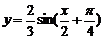
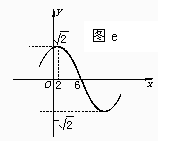 C
C
 D
D
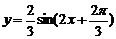
4 函数y=Asin(ωx+φ)(A>0,ω>0)在同一周期内,当x=
函数y=Asin(ωx+φ)(A>0,ω>0)在同一周期内,当x=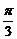 时,有ymax=2,当x=0时,有ymin=-2?,则函数表达式是
时,有ymax=2,当x=0时,有ymin=-2?,则函数表达式是 
 5
5 如图d是f(x)=Asin(ωx+φ),A>0,|φ|<
如图d是f(x)=Asin(ωx+φ),A>0,|φ|< 的一段图象,则函数f(x)的表达式为
的一段图象,则函数f(x)的表达式为 
6 如图e,是f(x)=Asin(ωx+φ),A>0,|φ|<
如图e,是f(x)=Asin(ωx+φ),A>0,|φ|< 的一段图象,则f(x)的表达式为
的一段图象,则f(x)的表达式为

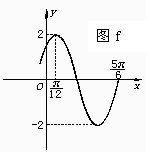
7 如图f所示的曲线是y=Asin(ωx+φ)(A>0,ω>0)的图象的一部分,求这个函数的解析式
如图f所示的曲线是y=Asin(ωx+φ)(A>0,ω>0)的图象的一部分,求这个函数的解析式
 8
8 函数y=Asin(ωx+φ)+k(A>0,ω>0)在同一周期内,当x=
函数y=Asin(ωx+φ)+k(A>0,ω>0)在同一周期内,当x=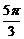 时,y有最大值为
时,y有最大值为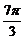 ,当x=
,当x=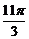 时,y有最小值-
时,y有最小值-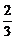 ,求此函数的解析式
,求此函数的解析式
9 已知f(x)=sin(x+θ)+
已知f(x)=sin(x+θ)+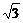 cos(x-θ)为偶函数,求θ的值
cos(x-θ)为偶函数,求θ的值
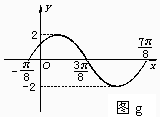
10. 由图g所示函数图象,求y=Asin(ωx+φ)
由图g所示函数图象,求y=Asin(ωx+φ)
(|φ|<π)的表达式
选题意图:考查数形结合的思想方法

两种方法殊途同归


 (1) y=sinx相位变换y=sin(x+φ)周期变换y=sin(ωx+φ)振幅变换
(1) y=sinx相位变换y=sin(x+φ)周期变换y=sin(ωx+φ)振幅变换
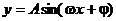
(2)y=sinx周期变换 y=sinωx相位变换 y=sin(ωx+φ)振幅变换



1 已知函数y=Asin(ωx+
已知函数y=Asin(ωx+ )(A>0,ω>0,0<
)(A>0,ω>0,0< <2π)图象的一个最高点(2,
<2π)图象的一个最高点(2,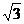 ),由这个最高点到相邻最低点的图象与x轴交于点(6,0),试求函数的解析式
),由这个最高点到相邻最低点的图象与x轴交于点(6,0),试求函数的解析式
解:由已知可得函数的周期T=4×(6-2)=16
∴ω= =
=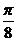
又A=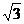 ∴y=
∴y=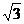 sin(
sin(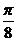 x+
x+ )
)
把(2,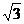 )代入上式得:
)代入上式得: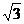 =sin(
=sin(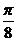 ×2+
×2+ )·
)·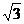
∴sin(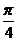 +
+ )=1,而0<
)=1,而0< <2π ∴
<2π ∴ =
=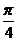
∴所求解析式为:y=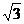 sin(
sin(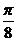 x+
x+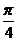 )
)
2 已知函数y=Asin(ωx+
已知函数y=Asin(ωx+ )(其中A>0,|
)(其中A>0,| |<
|<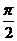 )在同一周期内,当x=
)在同一周期内,当x=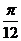 时,y有最小值-2,当x=
时,y有最小值-2,当x=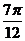 时,y有最大值2,求函数的解析式
时,y有最大值2,求函数的解析式
分析:由y=Asin(ωx+φ)的图象易知A的值,在同一周期内,最高点与最低点横坐标之间的距离即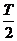 ,由此可求ω的值,再将最高(或低)点坐标代入可求
,由此可求ω的值,再将最高(或低)点坐标代入可求

解:由题意A=2,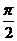 =
=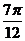 -
-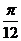 ∴T=π=
∴T=π=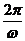 ,∴ω=2
,∴ω=2
∴y=2sin(2x+ )又x=
)又x=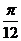 时y=2
时y=2
∴2=2sin(2×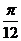 +
+ )
)
∴ +
+ =
=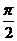
 <
<
∴ =
=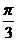
∴函数解析式为:y=2sin(2x+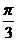 )
)
3 若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,然后再将整个图象沿x轴向左平移
若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,然后再将整个图象沿x轴向左平移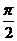 个单位,沿y轴向下平移1个单位,得到函数y=
个单位,沿y轴向下平移1个单位,得到函数y=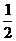 sinx的图象,则有y=f(x)是( )
sinx的图象,则有y=f(x)是( )
A y=
y=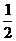 sin(2x+
sin(2x+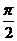 )+1
B
)+1
B y=
y=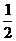 sin(2x-
sin(2x-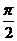 )+1
)+1
C y=
y=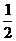 sin(2x-
sin(2x-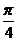 )+1
D
)+1
D y=
y=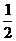 sin(
sin(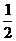 x+
x+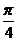 )+1
)+1
解析:由题意可知
y=f[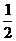 (x+
(x+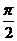 )]-1=
)]-1=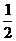 sinx
sinx
即y=f[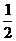 (x+
(x+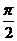 )]=
)]=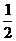 sinx+1
sinx+1
令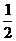 (x+
(x+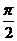 )=t,则x=2t-
)=t,则x=2t-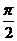
∴f(t)=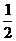 sin(2t-
sin(2t-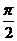 )+1
)+1
∴f(x)=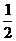 sin(2x-
sin(2x-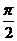 )+1 答案:B
)+1 答案:B
4 函数y=3sin(2x+
函数y=3sin(2x+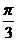 )的图象,可由y=sinx的图象经过下述哪种变换而得到 ( ) 答案:B
)的图象,可由y=sinx的图象经过下述哪种变换而得到 ( ) 答案:B
A 向右平移
向右平移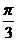 个单位,横坐标缩小到原来的
个单位,横坐标缩小到原来的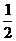 倍,纵坐标扩大到原来的3倍
倍,纵坐标扩大到原来的3倍
B 向左平移
向左平移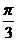 个单位,横坐标缩小到原来的
个单位,横坐标缩小到原来的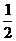 倍,纵坐标扩大到原来的3倍
倍,纵坐标扩大到原来的3倍
C 向右平移
向右平移 个单位,横坐标扩大到原来的2倍,纵坐标缩小到原来的
个单位,横坐标扩大到原来的2倍,纵坐标缩小到原来的 倍
倍
D 向左平移
向左平移 个单位,横坐标缩小到原来的
个单位,横坐标缩小到原来的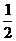 倍,纵坐标缩小到原来的
倍,纵坐标缩小到原来的 倍
倍
例1 画出函数y=3sin(2x+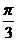 ),x∈R的简图
),x∈R的简图
解:(五点法)由T=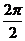 ,得T=π 列表:
,得T=π 列表:
|
x |
– |
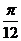 |
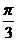 |
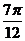 |
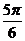 |
2x+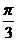 |
0 |
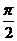 |
π |
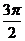 |
2π |
3sin(2x+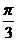 |
0 |
3 |
0 |
–3 |
0 |
描点画图:

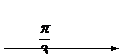 这种曲线也可由图象变换得到:
这种曲线也可由图象变换得到:
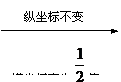
即:y=sinx
y=sin(x+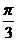 )
)

y=sin(2x+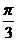 ) y=3sin(2x+
) y=3sin(2x+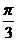 )
)
一般地,函数y=Asin(ωx+ ),x∈R(其中A>0,ω>0)的图象,可以看作用下面的方法得到:
),x∈R(其中A>0,ω>0)的图象,可以看作用下面的方法得到:
先把正弦曲线上所有的点向左(当 >0时)或向右(当
>0时)或向右(当 <0时=平行移动|
<0时=平行移动| |个单位长度,再把所得各点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的
|个单位长度,再把所得各点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的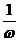 倍(纵坐标不变),再把所得各点的纵坐标伸长(当A>1时)或缩短(当0<A<1时)到原来的A倍(横坐标不变)
倍(纵坐标不变),再把所得各点的纵坐标伸长(当A>1时)或缩短(当0<A<1时)到原来的A倍(横坐标不变)
另外,注意一些物理量的概念:
A :称为振幅;T=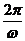 :称为周期;f=
:称为周期;f=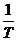 :称为频率;
:称为频率;
ωx+ :称为相位
:称为相位 x=0时的相位
x=0时的相位 称为初相
称为初相
评述:由y=sinx的图象变换出y=sin(ωx+ )的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换
)的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换
途径一:先平移变换再周期变换(伸缩变换)
先将y=sinx的图象向左( >0)或向右(
>0)或向右( <0=平移|
<0=平移| |个单位,再将图象上各点的横坐标变为原来的
|个单位,再将图象上各点的横坐标变为原来的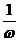 倍(ω>0),便得y=sin(ωx+
倍(ω>0),便得y=sin(ωx+ )的图象
)的图象
途径二:先周期变换(伸缩变换)再平移变换
先将y=sinx的图象上各点的横坐标变为原来的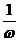 倍(ω>0),再沿x轴向左(
倍(ω>0),再沿x轴向左( >0)或向右(
>0)或向右( <0=平移
<0=平移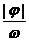 个单位,便得y=sin(ωx+
个单位,便得y=sin(ωx+ )的图象
)的图象
例2已知如图是函数y=2sin(ωx+ )其中|
)其中| |<
|<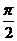 的图象,那么
的图象,那么
 A
A ω=
ω=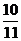 ,
, =
= B
B ω=
ω=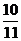 ,
, =-
=-
C ω=2,
ω=2, =
= D
D ω=2,
ω=2, =-
=-
解析:由图可知,点(0,1)和点(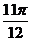 ,0)都是图象上的点
,0)都是图象上的点 将点(0,1)的坐标代入待定的函数式中,得2sin
将点(0,1)的坐标代入待定的函数式中,得2sin =1,即sin
=1,即sin =
=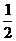 ,又|
,又| |<
|<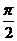 ,∴
,∴ =
=
又由“五点法”作图可知,点(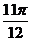 ,0)是“第五点”,所以ωx+
,0)是“第五点”,所以ωx+ =2π,即ω·
=2π,即ω·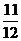 π+
π+ =2π,解之得ω=2,故选C
=2π,解之得ω=2,故选C
解此题时,若能充分利用图象与函数式之间的联系,则也可用排除法来巧妙求解,即:
解:观察各选择答案可知,应有ω>0
观察图象可看出,应有T=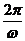 <2π,∴ω>1 ,故可排除A与B
<2π,∴ω>1 ,故可排除A与B
由图象还可看出,函数y=2sin(ωx+ )的图象是由函数y=2sinωx的图象向左移而得到的
∴
)的图象是由函数y=2sinωx的图象向左移而得到的
∴ >0,又可排除D,故选C
>0,又可排除D,故选C
例3已知函数y=Asin(ωx+ ),在同一周期内,当x=
),在同一周期内,当x=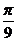 时函数取得最大值2,当x=
时函数取得最大值2,当x=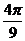 时函数取得最小值-2,则该函数的解析式为( )
时函数取得最小值-2,则该函数的解析式为( )
A y=2sin(3x-
y=2sin(3x- )
B
)
B y=2sin(3x+
y=2sin(3x+ )
)
C y=2sin(
y=2sin(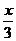 +
+ )
D
)
D y=2sin(
y=2sin(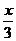 -
- )
)
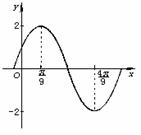 解析:由题设可知,所求函数的图象如图所示,点(
解析:由题设可知,所求函数的图象如图所示,点(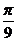 ,2)和点(
,2)和点(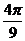 ,-2)都是图象上的点,且由“五点法”作图可知,这两点分别是“第二点”和“第四点”,所以应有:
,-2)都是图象上的点,且由“五点法”作图可知,这两点分别是“第二点”和“第四点”,所以应有:
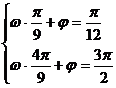 解得
解得 答案:B
答案:B
由y=Asin(ωx+ )的图象求其函数式:
)的图象求其函数式:
一般来说,在这类由图象求函数式的问题中,如对所求函数式中的A、ω、 不加限制(如A、ω的正负,角
不加限制(如A、ω的正负,角 的范围等),那么所求的函数式应有无数多个不同的形式(这是由于所求函数是周期函数所致),因此这类问题多以选择题的形式出现,我们解这类题的方法往往因题而异,但逆用“五点法”作图的思想却渗透在各不同解法之中
的范围等),那么所求的函数式应有无数多个不同的形式(这是由于所求函数是周期函数所致),因此这类问题多以选择题的形式出现,我们解这类题的方法往往因题而异,但逆用“五点法”作图的思想却渗透在各不同解法之中
2.周期变换:函数y=sinωx, xÎR (ω>0且ω¹1)的图象,可看作把正弦曲线上所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的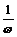 倍(纵坐标不变).若ω<0则可用诱导公式将符号“提出”再作图
倍(纵坐标不变).若ω<0则可用诱导公式将符号“提出”再作图 ω决定了函数的周期
ω决定了函数的周期
3 相位变换: 函数y=sin(x+
相位变换: 函数y=sin(x+ ),x∈R(其中
),x∈R(其中 ≠0)的图象,可以看作把正弦曲线上所有点向左(当
≠0)的图象,可以看作把正弦曲线上所有点向左(当 >0时)或向右(当
>0时)或向右(当 <0时=平行移动|
<0时=平行移动| |个单位长度而得到
|个单位长度而得到 (用平移法注意讲清方向:“加左”“减右”)
(用平移法注意讲清方向:“加左”“减右”)
1.振幅变换:y=Asinx,xÎR(A>0且A¹1)的图象可以看作把正数曲线上的所有点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍得到的 它的值域[-A, A] 最大值是A, 最小值是-A.若A<0 可先作y=-Asinx的图象 ,再以x轴为对称轴翻折
它的值域[-A, A] 最大值是A, 最小值是-A.若A<0 可先作y=-Asinx的图象 ,再以x轴为对称轴翻折 A称为振幅
A称为振幅
|
16.(本小题13分) (1) 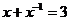 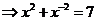 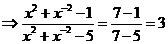 (2)解析:设F(x)=f(x)-2,即F(x)=alog2x+blog3x, 则F()=alog2+blog3=-(alog2x+blog3x)=-F(x), ∴F(2010)=-F()=-[f()-2]=-2, 即f(2010)-2=-2,故f(2010)=0 |
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效!
|
17.(本小题13分) A={x|-1<x≤5}. (1) 当m=3时,B={x|-1<x<3}, 则∁RB={x|x≤-1或x≥3}, ∴A∩(∁RB)={x|3≤x≤5}. (2)∵A={x|-1<x≤5},A∩B={x|-1<x<4}, ∴有-42+2×4+m=0,解得m=8, 此时B={x|-2<x<4},符合题意. |
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效
|
18.(本小题13分) (1)证明:∵f(x+2)=-f(x), ∴f(x+4)=-f(x+2)=-[-f(x)]=f(x), ∴f(x)是以4为周期的周期函数. (2)当0≤x≤1时,f(x)=x, 设-1≤x≤0,则0≤-x≤1, ∴f(-x)=(-x)=-x.∵f(x)是奇函数, ∴f(-x)=-f(x),∴-f(x)=-x, 即f(x)=x.故f(x)=x(-1≤x≤1) 又设1<x<3,则-1<x-2<1, ∴f(x-2)=(x-2), 又∵f(x-2)=-f(2-x)=-f[(-x)+2] =-[-f(-x)]=-f(x), ∴-f(x)=(x-2), ∴f(x)=-(x-2)(1<x<3). ∴f(x)= 由f(x)=-,解得x=-1.∵f(x)是以4为周期的周期函数.故f(x)=-的所有x=4n-1(n∈Z).令0≤4n-1≤2010,则≤n≤502,又∵n∈Z,∴1≤n≤502(n∈Z),∴在[0,2010]上共有502个x使f(x)=-. |
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效!
|
19.(本小题13分) (1)由已知得,函数的定义域为 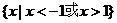 , ,关于原点对称; 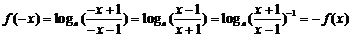 故  是偶函数。 是偶函数。(2)当 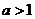 时,在定义域 时,在定义域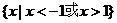 内,函数 内,函数 与函数 与函数 的单调性一致; 的单调性一致; , ,易得, 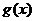 分别在区间 分别在区间 内为单调递减。 内为单调递减。所以,函数  区间 区间 内为单调递减; 内为单调递减;(3)由已知得 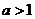 ,由(2)可知,函数 ,由(2)可知,函数 在 在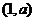 内单调递减,所以有 内单调递减,所以有 即 即 即  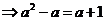 xsc解之得 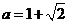 (负值舍去) (负值舍去) |
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效!
|
20.(本小题14分) (1)当甲的用水量不超过6吨时,即  时,乙的用水量也不会超过6吨,此时 时,乙的用水量也不会超过6吨,此时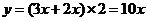 ; ;当甲的用水量超过6吨而乙的用水量没有超过6吨时,即 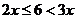 时,此时 时,此时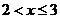 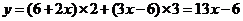 当甲乙的用水量都超过6吨时,即 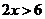 时, 时,此时 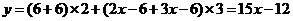 综上可知, 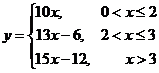 (2)若 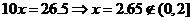 (舍去) (舍去)若 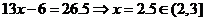 (符合题意) (符合题意)若 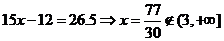 (舍去) (舍去)综上可知,甲的用水量为  (吨) (吨)付费 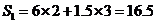 (元) (元)乙的用水量为  (吨) (吨)付费 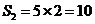 (元) (元)答:略。 |

 请在各题规定的黑色矩形区域内答题,超出该区域的答案无效!
请在各题规定的黑色矩形区域内答题,超出该区域的答案无效!
|
21.(本小题7+7=14分) (1) 法一:特殊点法 在直线 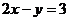 上任取两点(2、1)和(3、3),……1分 上任取两点(2、1)和(3、3),……1分则 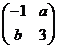 · · 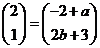 即得点 即得点 …3 分 …3 分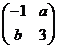 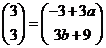 即得点 即得点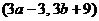 将 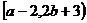 和 和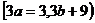 分别代入 分别代入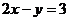 上得 上得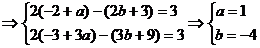 则矩阵 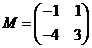 则 则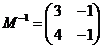 法二:通法 设  为直线 为直线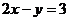 上任意一点其在M的作用下变为 上任意一点其在M的作用下变为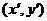 则 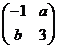 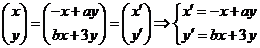 代入 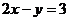 得: 得: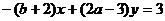 其与 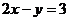 完全一样得 完全一样得 则矩阵 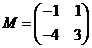 则 则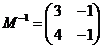 (2) 解:(Ⅰ)消去参数 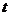 ,得直线 ,得直线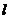 的普通方程为 的普通方程为 …3分 …3分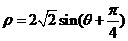 ,即 ,即 , ,两边同乘以  得 得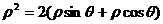 , ,得⊙ 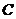 的直角坐标方程为 的直角坐标方程为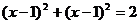 ………5分 ………5分(Ⅱ)圆心 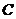 到直线 到直线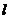 的距离 的距离 ,所以直线 ,所以直线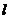 和⊙ 和⊙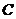 相交…7分 相交…7分(3).解:由 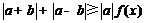 ,且 ,且 , ,得 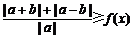 ……3分 ……3分又因为 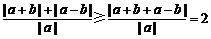 ,则有2 ,则有2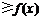 ………5分 ………5分解不等式  ,得 ,得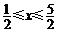 …………………… 7分 …………………… 7分 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com