
2.(x-1)11展开式中x的偶次项系数之和是( )
A.-2048 B.-1023 C.-1024 D.1024
1.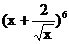 展开式中常数项是( )
展开式中常数项是( )
A.第4项 B.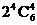 C.
C. D.2
D.2
例1.(1)求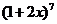 的展开式的第四项的系数;
(2)求
的展开式的第四项的系数;
(2)求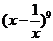 的展开式中
的展开式中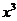 的系数及二项式系数
的系数及二项式系数
解: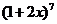 的展开式的第四项是
的展开式的第四项是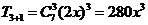 ,
∴
,
∴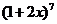 的展开式的第四项的系数是
的展开式的第四项的系数是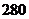 .
.
(2)∵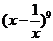 的展开式的通项是
的展开式的通项是 ,
,
∴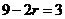 ,
, ,
,
∴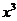 的系数
的系数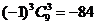 ,
,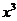 的二项式系数
的二项式系数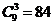 .
.
例2.求 的展开式中
的展开式中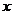 的系数
的系数
分析:要把上式展开,必须先把三项中的某两项结合起来,看成一项,才可以用二项式定理展开,然后再用一次二项式定理,,也可以先把三项式分解成两个二项式的积,再用二项式定理展开
解:(法一)
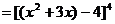
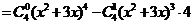
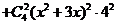
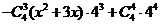 ,
,
显然,上式中只有第四项中含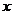 的项,
的项,
∴展开式中含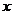 的项的系数是
的项的系数是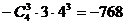
(法二):

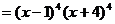
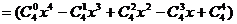
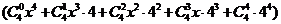
∴展开式中含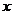 的项的系数是
的项的系数是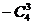
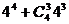
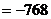 .
.
例3.已知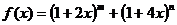
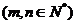 的展开式中含
的展开式中含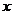 项的系数为
项的系数为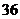 ,求展开式中含
,求展开式中含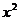 项的系数最小值
项的系数最小值
分析:展开式中含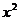 项的系数是关于
项的系数是关于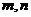 的关系式,由展开式中含
的关系式,由展开式中含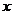 项的系数为
项的系数为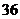 ,可得
,可得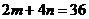 ,从而转化为关于
,从而转化为关于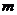 或
或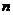 的二次函数求解
的二次函数求解
解: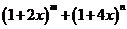 展开式中含
展开式中含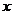 的项为
的项为
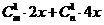

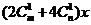
∴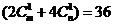 ,即
,即 ,
,
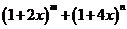 展开式中含
展开式中含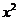 的项的系数为
的项的系数为

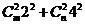
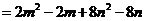 ,
,
∵ , ∴
, ∴ ,
,
∴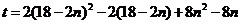

 ,∴当
,∴当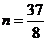 时,
时,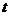 取最小值,但
取最小值,但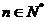 ,
,
∴ 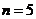 时,
时, 即
即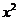 项的系数最小,最小值为
项的系数最小,最小值为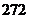 ,此时
,此时 .
.
例4.已知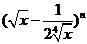 的展开式中,前三项系数的绝对值依次成等差数列,
的展开式中,前三项系数的绝对值依次成等差数列,
(1)证明展开式中没有常数项;(2)求展开式中所有的有理项
解:由题意: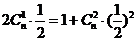 ,即
,即 ,∴
,∴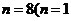 舍去)
舍去)
∴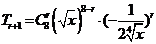
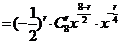


①若 是常数项,则
是常数项,则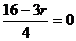 ,即
,即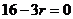 ,
,
∵ ,这不可能,∴展开式中没有常数项;
,这不可能,∴展开式中没有常数项;
②若 是有理项,当且仅当
是有理项,当且仅当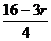 为整数,
为整数,
∴ ,∴
,∴ 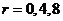 ,
,
即 展开式中有三项有理项,分别是: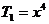 ,
, ,
,

2.二项展开式的通项公式: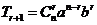

1.二项式定理及其特例:
(1) ,
,
(2) .
.
(三)填写下列名篇名句中的空缺(任选5空,超过5空的以前5空计分)。(5分)
13.(1)____________________,更那堪冷落清秋节。(柳永《雨霖铃》)
(2)____________________,月涌大江流。(杜甫《旅夜书怀》)
(3)玉鉴琼田三万顷,____________________。(张孝祥《念奴娇》)
(4)《出师》一表真名世,____________________?(陆游《书愤》)
(5)有志矣,____________,____________,亦不能至也。(王安石《游褒禅山记》)
(6)工欲善其事,____________________。(《论语》)
(7)竭诚则吴越为一体,____________________。(魏征《谏太宗十思疏》)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com