
例1、求函数 的最大值和最小值.
的最大值和最小值.
例2、在平面直角坐标系中有点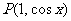 ,
,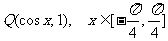 .
.
(1)求向量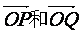 的夹角
的夹角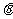 的余弦值用
的余弦值用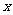 表示的函数
表示的函数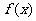 ;
;
(2)求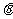 的最值.
的最值.
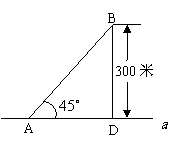
例3、如图,某海滨浴场的岸边可近似地看作直线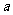 ,救生员现在岸边的A处,发现海中的B处有人求救,救生员没有直接从A处游向B处,而是沿岸边A跑到离B最近的D处,然后游向B处,若救生员在岸边的行进速度为6米/秒,在海水中的行进速度为2米/秒.
,救生员现在岸边的A处,发现海中的B处有人求救,救生员没有直接从A处游向B处,而是沿岸边A跑到离B最近的D处,然后游向B处,若救生员在岸边的行进速度为6米/秒,在海水中的行进速度为2米/秒.
(1)分析救生员的选择是否正确?
(2)在AD上找一处C,使救生员从A到B的时间最短,并求出最短时间。
例4、已知函数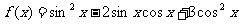 。
。
(1)证明:当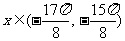 时,经过
时,经过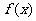 图象上的任意两点的直线的斜率恒为负数;
图象上的任意两点的直线的斜率恒为负数;
(2)设有不相等的实数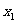 ,
,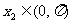 ,且
,且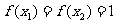 ,求
,求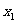 +
+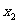 的值。
的值。
例5、(05山东卷)已知向量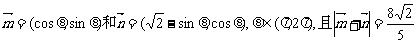 ,
,
求 的值.
的值.
5、设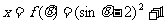 ,则
,则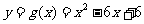 的最大值是
,最小值是
.
的最大值是
,最小值是
.
4、函数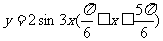 与函数
与函数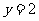 的图象围成一个封闭图形,这个封闭图形的面积是
.
的图象围成一个封闭图形,这个封闭图形的面积是
.
3、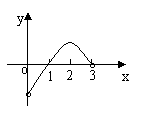 已知
已知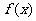 是定义在(0,3)上的函数,图象如图所示,那么不等式
是定义在(0,3)上的函数,图象如图所示,那么不等式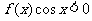 的解集是
( )
的解集是
( )
A、 B、
B、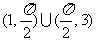
C、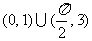 D、
D、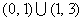
2、设实数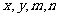 满足
满足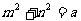 ,
,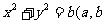 是正常数,且
是正常数,且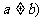 ,那么
,那么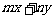 的最大值是
( )
的最大值是
( )
A、 B、
B、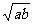 C、
C、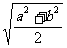 D、
D、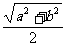
1、直线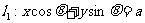 ,
, ,当
,当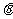 变化时,
变化时,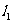 与
与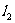 交点的轨迹是
( )
交点的轨迹是
( )
A、直线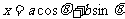 B、直线
B、直线
C、圆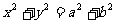 D、无法确定
D、无法确定
三角函数是一种应用十分广泛的函数,常将一些代数问题、几何问题或某些实际应用问题通过三角代换,利用转化和化归的思想方法转化为三角问题来求解。
10. 在△ABC中,sinA= ,判断这个三角形的形状.
,判断这个三角形的形状.
分析:判断一个三角形的形状,可由三个内角的关系确定,亦可由三边的关系确定.采用后一种方法解答本题,就必须“化角为边”.
解:应用正弦定理、余弦定理,可得
a=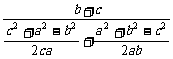 ,所以
,所以
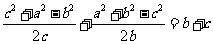 ,
,
化简得a2=b2+c2.所以△ABC是直角三角形.
评述:恒等变形是学好数学的基本功,变形的方向是关键.若考虑三内角的关系,本题可以从已知条件推出cosA=0.
[探索题]已知A、B、C是△ABC的三个内角,y=cotA+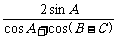 .
.
(1)若任意交换两个角的位置,y的值是否变化?试证明你的结论.
(2)求y的最小值.
解:(1)∵y=cotA+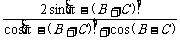
=cot A+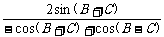
=cot A+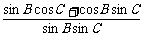
=cotA+cotB+cotC,
∴任意交换两个角的位置,y的值不变化.
(2)∵cos(B-C)≤1,
∴y≥cotA+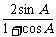 =
=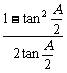 +2tan
+2tan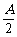 =
=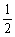 (cot
(cot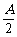 +3tan
+3tan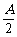 )≥
)≥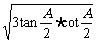 =
=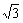 .
.
故当A=B=C=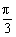 时,ymin=
时,ymin=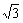 .
.
评述:本题的第(1)问是一道结论开放型题,y的表达式的表面不对称性显示了问题的有趣之处.第(2)问实际上是一道常见题:在△ABC中,求证:cotA+cotB+cotC≥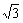 .
.
可由三数的均值不等式结合cotA+cotB+cotC =cotAcotBcotC来证.
9. (2004全国Ⅱ)已知锐角△ABC中,sin(A+B)= ,sin(A-B)=
,sin(A-B)=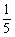 .
.
(1)求证:tanA=2tanB;
(2)设AB=3,求AB边上的高.
剖析:有两角的和与差联想到两角和与差的正弦公式,结合图形,以(1)为铺垫,解决(2).
(1)证明:∵sin(A+B)= ,sin(A-B)=
,sin(A-B)=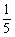 ,
,
∴
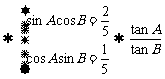 =2.
=2.
∴tanA=2tanB.
(2)解: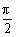 <A+B<π,∴sin(A+B)=
<A+B<π,∴sin(A+B)= .
.
∴tan(A+B)=-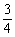 ,
,
即 =-
=-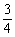 .将tanA=2tanB代入上式整理得2tan2B-4tanB-1=0,解得tanB=
.将tanA=2tanB代入上式整理得2tan2B-4tanB-1=0,解得tanB= (负值舍去).得tanB=
(负值舍去).得tanB=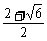 ,∴tanA=2tanB=2+
,∴tanA=2tanB=2+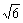 .
.
设AB边上的高为CD,则AB=AD+DB=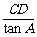 +
+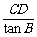 =
=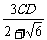 .由AB=3得CD=2+
.由AB=3得CD=2+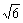 ,所以AB边上的高为2+
,所以AB边上的高为2+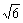 .
.
评述:本题主要考查三角函数概念,两角和与差的公式以及应用,分析和计算能力.
8.(2005春北京)在△ABC中,sinA+cosA=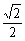 ,AC=2,AB=3,求tanA的值和△ABC的面积.
,AC=2,AB=3,求tanA的值和△ABC的面积.
解法一:∵sinA+cosA=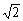 cos(A-45°)=
cos(A-45°)=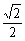 ,
,
∴cos(A-45°)=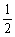 .
.
又0°<A<180°,
∴A-45°=60°,A=105°.
∴tanA=tan(45°+60°)=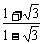 =-2-
=-2-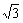 .
.
∴sinA=sin105°=sin(45°+60°)
=sin45°cos60°+cos45°sin60°=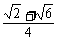 .
.
∴S△ABC=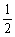 AC·ABsinA
AC·ABsinA
=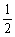 ·2·3·
·2·3·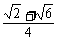
=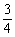 (
(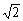 +
+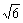 ).
).
解法二:∵sinA+cosA=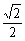 , ①
, ①
∴(sinA+cosA)2=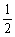 .∴2sinAcosA=-
.∴2sinAcosA=-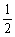 .
.
∵0°<A<180°,∴sinA>0,cosA<0.
∴90°<A<180°.
∵(sinA-cosA)2=1-2sinAcosA=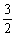 ,
,
∴sinA-cosA=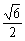 . ②
. ②
①+②得sinA=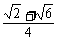 .
.
①-②得cosA=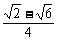 .
.
∴tanA=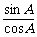 =
=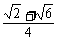 ·
·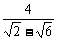 =-2-
=-2-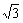 .
.
(以下同解法一)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com