
例1、已知x>0,y>0且x+2y=1,求xy的最大值,及xy取最大值时的x、y的值.
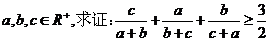
例2
例3、已知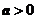 ,求函数
,求函数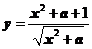 的最小值。
的最小值。
例4、设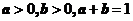 ,求证:
,求证:
(1) ; (2)
; (2)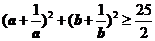 ;
;
(3)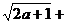
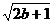 ≤
≤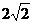 (4)(
(4)( )(
)(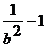 )≥9
)≥9
(5)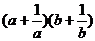 ≥
≥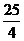
例5、(05江苏卷)设数列{an}的前项和为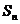 ,已知a1=1,
a2=6, a3=11,且
,已知a1=1,
a2=6, a3=11,且
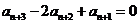 ,
, 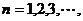
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)证明不等式 .
.
8、已知x>0,y>0且x+y=5,则lgx+lgy的最大值是 .
若正数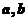 满足
满足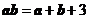 ,则
,则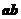 的取值范围是_____________________.
的取值范围是_____________________.
7、函数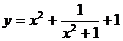 的值域为
.
的值域为
.
6、若实数a、b满足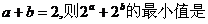 ( )
( )
A.8 B.4 C.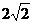 D.
D.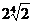
5、若 则下列不等式中正确的是( )
则下列不等式中正确的是( )
A.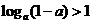 B.
B. C.
C. D.
D.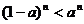
3、设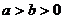 ,则下列不等式成立的是 ( )
,则下列不等式成立的是 ( )
A.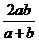
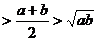 B.
B.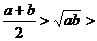
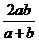
C.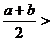
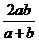
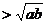 D.
D.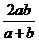
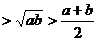
2、下列函数中,最小值为2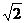 的是 (
)
的是 (
)
A.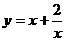 B.
B.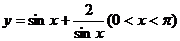
C.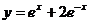 D.
D.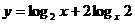
1、(05福建卷)下列结论正确的是 ( )
A.当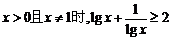 B.
B.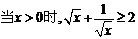
C.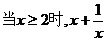 的最小值为2 D.当
的最小值为2 D.当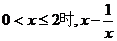 无最大值
无最大值
2.几个著名不等式
(1)平均不等式: 如果a,b都是正数,那么 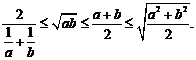 (当仅当a=b时取等号)
(当仅当a=b时取等号)
(2)柯西不等式: 
(3)琴生不等式(特例)与凸函数、凹函数
若定义在某区间上的函数f(x),对于定义域中任意两点 有
有
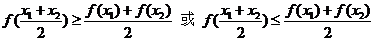
则称f(x)为凸(或凹)函数.
1.几个重要不等式
(1)
(2)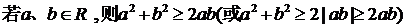 (当仅当a=b时取等号)
(当仅当a=b时取等号)
(3)如果a,b都是正数,那么 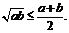 (当仅当a=b时取等号)
(当仅当a=b时取等号)
最值定理:若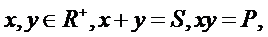 则:
则:
1如果P是定值, 那么当x=y时,S的值最小; 2如果S是定值, 那么当x=y时,P的值最大.
注意:
1前提:“一正、二定、三相等”,如果没有满足前提,则应根据题目创设情境;还要注意选择恰当的公式;
2“和定 积最大,积定 和最小”,可用来求最值;
3均值不等式具有放缩功能,如果有多处用到,请注意每处取等的条件是否一致。
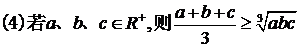 (当仅当a=b=c时取等号)
(当仅当a=b=c时取等号)
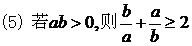 (当仅当a=b时取等号)
(当仅当a=b时取等号)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com