
8. 设有数列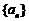 ,
,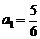 ,若以
,若以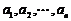 为系数的一元二次方程
为系数的一元二次方程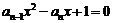
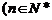 ,且
,且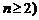 都有根
都有根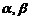 满足
满足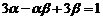 。
。
(1)求证:数列 是等比数列;
是等比数列;
(2)求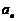 ;
;
(3)求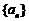 的前n项和
的前n项和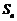 。
。
7. 已知等差数列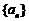 的公差
的公差 ,数列
,数列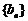 是等比数列,又
是等比数列,又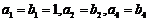 。
。
(1)求数列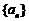 及
及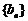 的通项公式;
的通项公式;
(2)设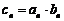 ,求数列
,求数列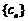 的前n项和
的前n项和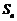 (写成关于n的表达式)。
(写成关于n的表达式)。
6. 用数字0, 1, 2, 3,
5组成没有重复数字的五位偶数,把这些偶数从小到大排列起来,得到一个数列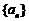 ,则
,则 。
。
5. 三个实数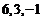 排成一行,在6和3之间插入两个实数,3和
排成一行,在6和3之间插入两个实数,3和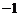 之间插入一个实数,使得这六个数中的前三个、后三个分别成等差数列,且插入的三个数本身依次成等比数列,那么所插入的这三个数的和可能是:①
之间插入一个实数,使得这六个数中的前三个、后三个分别成等差数列,且插入的三个数本身依次成等比数列,那么所插入的这三个数的和可能是:①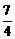 ;②3;③
;②3;③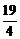 ;④7。其中正确的序号是
。
;④7。其中正确的序号是
。
4. 定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。
已知数列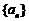 是等和数列,且
是等和数列,且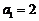 ,公和为5,那么
,公和为5,那么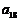 的值为______,这个数列的前n项
的值为______,这个数列的前n项
和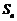 的计算公式为
。
的计算公式为
。
3. 等差数列所有项的和为210,其中前4项的和为40,后4项的和为80,则项数为 。
1. (05广东卷)已知数列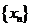 满足
满足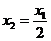 ,
,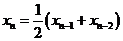 ,
,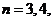 ….若
….若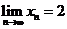 ,则 x1等于 (B)
,则 x1等于 (B)
(A)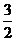 (B)3(C)4(D)5
(B)3(C)4(D)5
2. 已知等差数列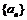 和等比数列
和等比数列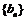 各项都是正数,且
各项都是正数,且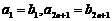 ,那么,一定有( )
,那么,一定有( )
A. C.
C.
1. 等差数列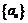 的前n项和为
的前n项和为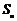 ,若
,若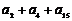 的值为常数,则下列各数中也是常数的是( )
的值为常数,则下列各数中也是常数的是( )
A.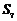 B.
B.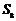 C.
C.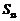 D.
D.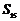
例1设无穷等差数列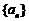 的前n项和为
的前n项和为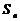 .
.
(1)若首项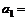 ,公差
,公差 ,求满足
,求满足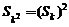 的正整数k;
的正整数k;
(2)求所有的无穷等差数列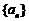 ,使得对于一切正整数k都有
,使得对于一切正整数k都有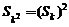 成立.
成立.
例2 如图,64个正数排成8行8列方阵.符号 表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都等于
表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都等于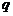 .若
.若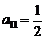 ,
,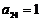 ,
,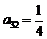 ,
,
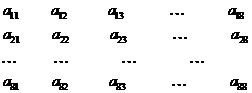 (1)求
(1)求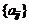 的通项公式;
的通项公式;
(2)记第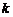 行各项和为
行各项和为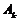 ,求
,求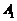 的值及数列
的值及数列
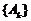 的通项公式;
的通项公式;
(3)若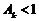 ,求
,求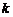 的值。
的值。
例3 函数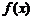 对任意
对任意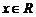 都有
都有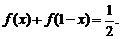
(1)求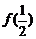 和
和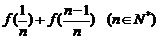 的值.
的值.
(2)数列 满足:
满足: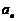 =
=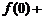
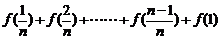 ,数列
,数列 是等差数列吗?
是等差数列吗?
(3)令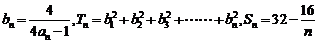 ,试比较
,试比较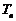 与
与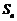 的大小.
的大小.
例4. (05福建卷)已知数列{an}满足a1=a, an+1=1+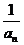 我们知道当a取不同的值时,得到不同的数列,如当a=1时,得到无穷数列:
我们知道当a取不同的值时,得到不同的数列,如当a=1时,得到无穷数列: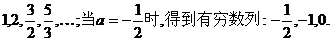
(Ⅰ)求当a为何值时a4=0;
(Ⅱ)设数列{bn}满足b1=-1,
bn+1=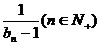 ,求证a取数列{bn}中的任一个数,都可以得到一个有穷数列{an};
,求证a取数列{bn}中的任一个数,都可以得到一个有穷数列{an};
(Ⅲ)若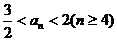 ,求a的取值范围.
,求a的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com