
6.已知两个正数a、b(a≠b)的等差中项为A,等比中项为B,则A与B的大小关系为_________.
5. (05重庆卷) 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2,且改塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是( )
(05重庆卷) 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2,且改塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是( )
(A) 4;
(B) 5;
(C) 6;
(D) 7。
4. (05湖南卷)已知数列{log2(an-1)}(n∈N*)为等差数列,且a1=3,a2=5,则
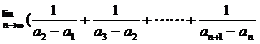 = ()
= ()
A.2 B. C.1 D.
C.1 D.
3、(04年上海卷.文理12)若干个能唯一确定一个数列的量称为该数列的“基本量”.设{an}是公比为q的无穷等比数列,下列{an}的四组量中,一定能成为该数列“基本量”的是第 组.(写出所有符合要求的组号)
①S1与S2; ②a2与S3; ③a1与an; ④q与an.
其中n为大于1的整数, Sn为{an}的前n项和.
2. 命题甲: 成等比数列,命题乙:
成等比数列,命题乙: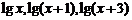 成等差数列,则甲是乙的
成等差数列,则甲是乙的
条件。(填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”)
1. 已知等比数列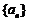 中,
中,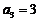 ,
, ,则该数列的通项公式
,则该数列的通项公式 。
。
3. 在等差数列{ }中,有关Sn 的最值问题:(1)当
}中,有关Sn 的最值问题:(1)当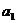 >0,d<0时,满足
>0,d<0时,满足 的项数m使得
的项数m使得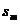 取最大值. (2)当
取最大值. (2)当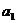 <0,d>0时,满足
<0,d>0时,满足 的项数m使得
的项数m使得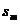 取最小值.在解含绝对值的 数列最值问题时,注意转化思想的应用。
取最小值.在解含绝对值的 数列最值问题时,注意转化思想的应用。
2. 判断和证明数列是等差(等比)数列常有三种方法:(1)定义法. (2)通项公式法.(3)中项公式法.
1. 等差数列和等比数列的概念、有关公式和性质
15、已知数列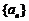 满足
满足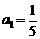 ,且当
,且当 ,
,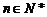 时,有
时,有 ,
,
(1)求证:数列 为等差数列;
为等差数列;
(2)试问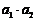 是否是数列
是否是数列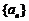 中的项?如果是,是第几项;如果不是,请说明理由。
中的项?如果是,是第几项;如果不是,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com