
例1(1)已知函数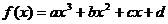 的图象如右图所示,则
的图象如右图所示,则
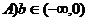
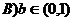

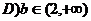
 (2)将函数
(2)将函数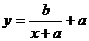 的图象向右平移2个单位后又向下平移2个单位,所得图象如果与原图象关于直线y=x对称,那么
( )
的图象向右平移2个单位后又向下平移2个单位,所得图象如果与原图象关于直线y=x对称,那么
( )
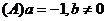
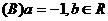
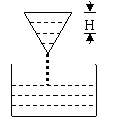
(3)如图,液体从一圆锥形漏斗漏入一圆柱形桶中,开始时漏斗盛满液体,经过3分钟漏完,若圆柱中液面上升速度是一常量,H是圆锥形漏斗中液面下落的距离,则H与下落时间分钟的函数关系表示的图象可能是 ( )

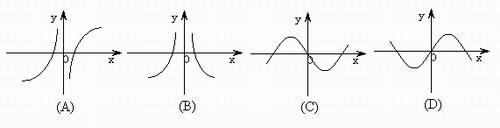
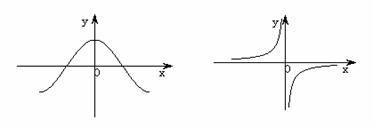 (4)已知函数y=f(x)和函数y=g(x)的图象如下:
(4)已知函数y=f(x)和函数y=g(x)的图象如下:
则函数y=f(x)g(x)的图象可能是
(5)设函数 的定义域为R,则函数
的定义域为R,则函数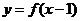 与
与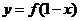 的图象关于( )
的图象关于( )
A、直线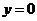 对称 B、直线
对称 B、直线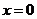 对称
对称
C、直线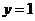 对称 D、直线
对称 D、直线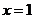 对称
对称
例2.作出下列函数的图象
(1)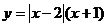 (2)
(2)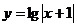 (3)
(3)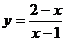
例3(1)方程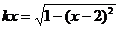 有两个不相等的实根,求实数k的取值范围
有两个不相等的实根,求实数k的取值范围
(2)若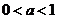 ,则方程
,则方程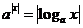 有几个实根
有几个实根
例4 设曲线C的方程是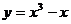 ,将C沿x轴,y轴正方向分别平行移动t,s单位长度后得曲线
,将C沿x轴,y轴正方向分别平行移动t,s单位长度后得曲线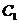 。 (1)写出曲线
。 (1)写出曲线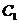 的方程;(2)证明曲线C与
的方程;(2)证明曲线C与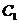 关于点
关于点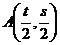 对称
对称
5、将函数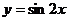 按向量
按向量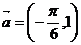 平移后的函数解析式是
平移后的函数解析式是
(A)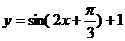 (B)
(B)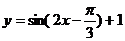
(C)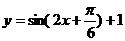 (D)
(D)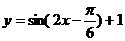
4、已知函数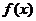 的图像关于直线
的图像关于直线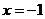 对称,且当
对称,且当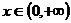 时,有
时,有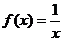 ,则当
,则当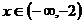 时,
时,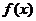 的解析式是
( )
的解析式是
( )
(A)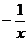 (B)
(B)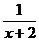 (C)
(C)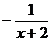 (D)
(D)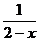
3、当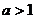 时,在同一坐标系中函数
时,在同一坐标系中函数 与
与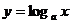 的图像是 (
)
的图像是 (
)

2、要得到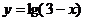 的图像,只需作
的图像,只需作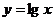 关于_____轴对称的图像,再向____平移3个单位而得到。
关于_____轴对称的图像,再向____平移3个单位而得到。
1、画出下列函数的图像
(1)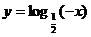 (2)
(2)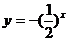 (3)
(3) (4)
(4)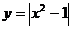
4.作函数图像的一般步骤是:
(1) 求出函数的定义域;(2)化简函数式;(3)讨论函数的性质(如奇偶性、周期性、单调性)以及图像上的特殊点、线(如极值点、渐近线、对称轴等);(4)利用基本函数的图像画出所给函数的图像。
3. 图象变换与变量替换的关系
(1)平移变换
(2)对称变换: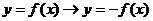 ,
, 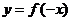 ,
,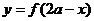 ,
,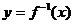 ,
, 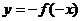 ,
,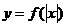 ,
,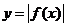
(3)伸缩变换: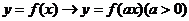 ,
, 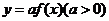
2. 正比例函数、反比例函数、二次函数的图象及几种基本初等函数的图象.
数形结合是中学数学的重要的数学思想方法,尤其是函数的图象更是历年高考的热点.函数图象是函数的一种表达形式,形象的显示了函数的性质,为研究数量关系提供了“形”的直观性,它是探求解题途径,获得问题的结果的重要工具.
1. 用描点法作函数的图象.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com