
1. 已知等差数列 满足
满足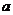
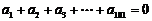 ,则有
,则有
A.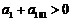 B.
B.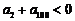 C.
C.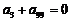 D.
D.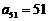
例1、设等差数列 、
、 的前n项和分别为
的前n项和分别为 、
、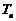 ,
,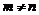 ,
,
1)若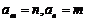 ,求
,求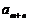 和
和 ;2)若
;2)若 ,求
,求 ;3)若
;3)若 ,求
,求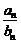 。
。
例2、①设等差数列 中,
中,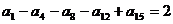 ,求
,求 及S15的值.
及S15的值.
②设等比数列 中,
中, ,前n项和Sn=126,求n和公比q.
,前n项和Sn=126,求n和公比q.
③等比数列中,q=2,S99=77,求 ;
;
④项数为奇数的等差数列 中,奇数项和为80,偶数项和为75,求此数列的中间项与项数.
中,奇数项和为80,偶数项和为75,求此数列的中间项与项数.
例3.是否存在公差不为零的等差数列{an},使对任意正整数n, 为常数?若存在,求出这个数列;若不存在,说明理由。
为常数?若存在,求出这个数列;若不存在,说明理由。
例4.三个实数10a2+81a+207,a+2,26-2a经适当排列,它们的常用对数值构成公差为1的等差数列。求a的值。
例5.已知递增的等比数列{an}前三项之积为512,它们分别减去1,3,9后,又构成等差数列.求证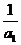 +
+ +
+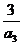 +…+
+…+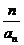 <1.
<1.
6.数列 是等比数列,下列四个命题:①
是等比数列,下列四个命题:① 、
、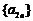 是等比数列;②
是等比数列;②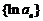 是等差数列;③
是等差数列;③ 、
、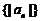 是等比数列;④
是等比数列;④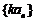 、
、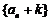
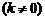 是等比数列。正确的命题是
。
是等比数列。正确的命题是
。
5.等比数列 中,①若a1 +a4=9,a2 ·a3=8,则前六项和S6=___________;②若a5+ a6 =a,a15+ a16 =b,则a25+ a26=__________________.
中,①若a1 +a4=9,a2 ·a3=8,则前六项和S6=___________;②若a5+ a6 =a,a15+ a16 =b,则a25+ a26=__________________.
4.在等差数列中,S11=22,则a6=__________________.
3.若一个等差数列的前3项和为34,最后3项和为146,且所有项的和为390,则这个数列有 项。
2.各项均为正数的等比数列 中,
中, ,则
,则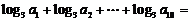 。
。
1.等差数列的前n项和为25,前2n项和为100,则它的前3n和为 。
3. 在等差数列{ }中,有关Sn
的最值问题:(1)当
}中,有关Sn
的最值问题:(1)当 >0,d<0时,满足
>0,d<0时,满足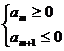 的项数m使得
的项数m使得 取最大值. (2)当
取最大值. (2)当 <0,d>0时,满足
<0,d>0时,满足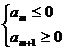 的项数m使得
的项数m使得 取最小值.在解含绝对值的数列最值问题时,注意转化思想的应用。
取最小值.在解含绝对值的数列最值问题时,注意转化思想的应用。
2. 判断和证明数列是等差(等比)数列常有三种方法:(1)定义法. (2)通项公式法.(3)中项公式法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com