
11.若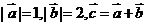 ,且
,且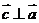 ,则向量
,则向量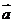 与
与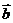 的夹角为________________.
的夹角为________________.
12
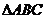 的三个内角为
的三个内角为 、
、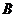 、
、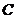 ,当
,当 为
时,
为
时,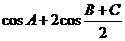 取得最大值,且这个最大值为________________.
取得最大值,且这个最大值为________________.
4.化简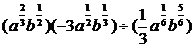 的结果是________________.
的结果是________________.
5
 ________________.
________________.
6 函数
函数 的最小正周期是________________.
的最小正周期是________________.
7 已知
已知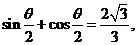 那么
那么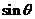 的值为 ,
的值为 ,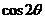 的值为
的值为

8 已知
已知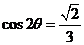 ,则
,则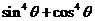 的值为________________.
的值为________________.
9 若
若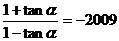 则
则 ________________.
________________.
10 设
设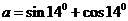 ,
,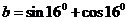 ,
,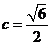 ,则
,则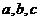 大小关系________________.
大小关系________________.
1.设集合A={1,2,3,4},B={0,1,2,4,5},全集U=A∪B,则集合∁U (A∩B)中的元素共有 ____________ 个.
2 已知
已知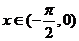 ,
,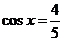 ,则
,则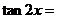 ________________.
________________.
3 在△ABC中,
在△ABC中,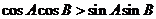 ,则△ABC为________________三角形.
,则△ABC为________________三角形.
2.已知下列不等式,比较正数m、n的大小:
(1)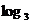 m<
m<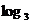 n
(2)
n
(2) 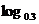 m>
m>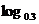 n
n
(3)  m<
m< n(0<a<1) (4)
n(0<a<1) (4)
 m>
m> n(a>1)
n(a>1)

解:(1)考查函数y=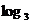 x
x
∵3>1,∴函数y=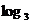 x在(0,+∞)是增函数
x在(0,+∞)是增函数
∵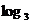 m<
m<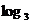 n,∴m<n
n,∴m<n
(2)考查函数y=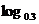 x
x
∵0<0.3<1,∴函数y=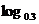 x在(0,+∞)上是减函数
x在(0,+∞)上是减函数
∵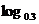 m>
m>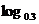 n,
n,
∴m<n
(3)考查函数y= x
x
∵0<a<1,
∴函数y= x在(0,+∞)上是减函数
x在(0,+∞)上是减函数
∵ m<
m< n,
n,
∴m>n
(4)考查函数y= x
x
∵a>1,
∴函数y= x在(0,+∞)上是增函数
x在(0,+∞)上是增函数
∵ m>
m> n,
n,
∴m>n
1.比较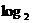 0.7与
0.7与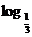 0.8两值大小
0.8两值大小
解:考查函数y=log2x
∵2>1,∴函数y=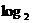 x在(0,+∞)上是增函数
x在(0,+∞)上是增函数
又0.7<1,∴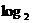 0.7<
0.7<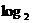 1=0
1=0
再考查函数y=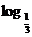 x
x
∵0<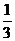 <1
<1
∴函数y=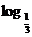 x在(0,+∞)上是减函数
x在(0,+∞)上是减函数
又1>0.8,∴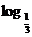 0.8>
0.8>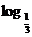 1=0
1=0
∴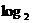 0.7<0<
0.7<0<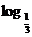 0.8
0.8
∴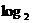 0.7<
0.7<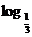 0.8
0.8
比较对数大小的方法,两种情况,求函数定义值域的方法
⑴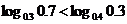

⑵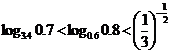

⑶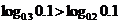

例1比较下列各组数中两个值的大小:
⑴ ;
⑵
;
⑵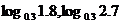 ;
;
⑶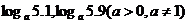

解:⑴考查对数函数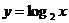 ,因为它的底数2>1,所以它在(0,+∞)上是增函数,于是
,因为它的底数2>1,所以它在(0,+∞)上是增函数,于是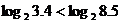

⑵考查对数函数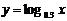 ,因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,于是
,因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,于是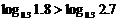

小结1:两个同底数的对数比较大小的一般步骤:
①确定所要考查的对数函数;
②根据对数底数判断对数函数增减性;
③比较真数大小,然后利用对数函数的增减性判断两对数值的大小
⑶当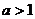 时,
时,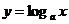 在(0,+∞)上是增函数,于是
在(0,+∞)上是增函数,于是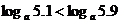
当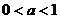 时,
时, 在(0,+∞)上是减函数,于是
在(0,+∞)上是减函数,于是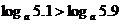
小结2:分类讨论的思想
对数函数的单调性取决于对数的底数是大于1还是小于1 而已知条件并未指明,因此需要对底数
而已知条件并未指明,因此需要对底数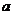 进行讨论,体现了分类讨论的思想,要求学生逐步掌握
进行讨论,体现了分类讨论的思想,要求学生逐步掌握
例3比较下列各组中两个值的大小:
⑴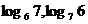 ;
⑵
;
⑵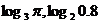

分析:由于两个对数值不同底,故不能直接比较大小,可在两对数值中间插入一个已知数,间接比较两对数的大小
解:⑴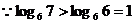 ,
, ,
,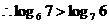

⑵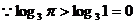 ,
,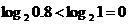 ,
,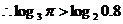 ;
;
小结3:引入中间变量比较大小
例3仍是利用对数函数的增减性比较两个对数的大小,当不能直接比较时,经常在两个对数中间插入1或0等,间接比较两个对数的大小
例4 求下列函数的定义域、值域:
⑴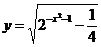 ⑵
⑵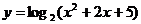
⑶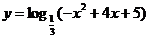 ⑷
⑷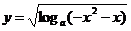
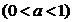

解:⑴要使函数有意义,则须:
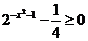 即:
即: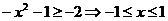
∵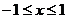 ∴
∴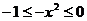 从而
从而 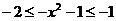
∴ ∴
∴ ∴
∴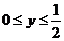
∴定义域为[-1,1],值域为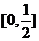

⑵∵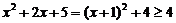 对一切实数都恒成立
对一切实数都恒成立
∴函数定义域为R
从而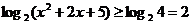 即函数值域为
即函数值域为

⑶要使函数有意义,则须:

由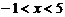 ∴在此区间内
∴在此区间内
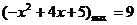
∴ 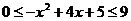

从而 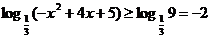 即:值域为
即:值域为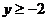
∴定义域为[-1,5],值域为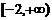

⑷要使函数有意义,则须: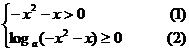
由①: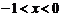
由②:∵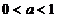 时 则须
时 则须 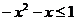 ,
,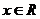
综合①②得 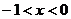

当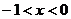 时
时 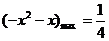 ∴
∴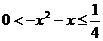
∴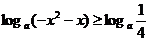 ∴
∴ 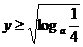
∴定义域为(-1,0),值域为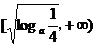

2、对数函数的性质:
|
|
a>1 |
0<a<1 |
|
图 象 |
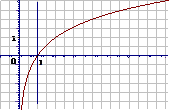 |
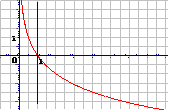 |
|
性 质 |
定义域:(0,+∞) |
|
值域:R |
||
过点(1,0),即当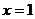 时, 时,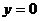  |
||
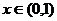 时 时 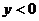  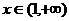 时 时 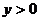  |
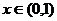 时 时 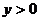  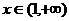 时 时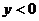  |
|
在(0,+∞)上是增函数 |
在(0,+∞)上是减函数 |
1、指对数互化关系::

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com