
1.求证: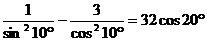 =32cos20°
=32cos20°
分析:本题证明方向显然是从左边证到右边 同时,注意到角与函数次数的变化,运用降幂公式sin2α=
同时,注意到角与函数次数的变化,运用降幂公式sin2α=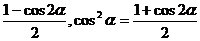 可使等式中的角与函数的次数得到统一
可使等式中的角与函数的次数得到统一
证法一:左边=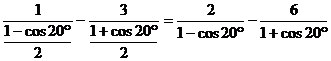
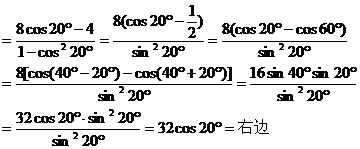
∴原式成立
证法二:左边=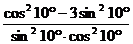

∴原式成立
评注:关于三角函数的化简、求值、证明问题要善于观察、联想公式之间的内在联系,通过拆、配等方法去分析问题和解决问题 证法一中的常值代换(
证法一中的常值代换(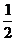 用cos60°代),角的分拆(20°分成40°-20°,60°分成40°+20°)及公式的逆用,是实施三角变形的重要方法
用cos60°代),角的分拆(20°分成40°-20°,60°分成40°+20°)及公式的逆用,是实施三角变形的重要方法
例1在△ABC中,已知cosA =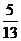 ,sinB =
,sinB =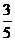 ,则cosC的值为…………(A)
,则cosC的值为…………(A)
A
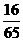 B
B
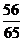 C
C
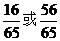 D
D

解:∵C = p - (A + B) ∴cosC = - cos(A + B)
又∵AÎ(0, p) ∴sinA = 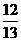 而sinB =
而sinB =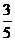 显然sinA > sinB
显然sinA > sinB
∴A
> B 即B必为锐角 ∴ cosB = 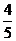
∴cosC
= - cos(A + B) = sinAsinB -
cosAcosB =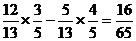
例2在△ABC中,ÐC>90°,则tanAtanB与1的关系适合………………(B)
A tanAtanB>1 B
tanAtanB>1 B tanAtanB>1 C
tanAtanB>1 C tanAtanB =1 D
tanAtanB =1 D 不确定
不确定
解:在△ABC中 ∵ÐC>90° ∴A, B为锐角 即tanA>0, tanB>0
又:tanC<0 于是:tanC
= -tan(A+B) = 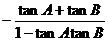 <0
<0
∴1 - tanAtanB>0 即:tanAtanB<1
又解:在△ABC中 ∵ÐC>90° ∴C必在以AB为直径的⊙O内(如图)
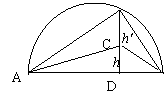
|
设CD = h,C’D = h’,AD = p,BD = q,
|
|
|
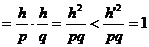
例3已知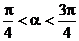 ,
,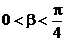 ,
,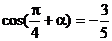 ,
, ,
,
求sin(a + b)的值
解:∵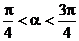 ∴
∴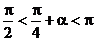
又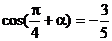 ∴
∴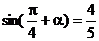
∵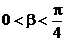 ∴
∴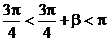
又 ∴
∴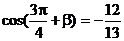
∴sin(a + b) = -sin[p + (a + b)] = 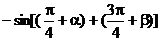
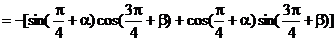
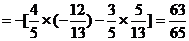
例4已知sina +
sinb = 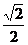 ,求cosa + cosb的范围
,求cosa + cosb的范围
解:设cosa + cosb = t,
则(sina +
sinb)2 + (cosa + cosb)2 = 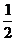 + t2
+ t2
∴2
+ 2cos(a - b) = 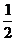 + t2
+ t2
即
cos(a - b) = 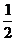 t2 -
t2 -
又∵-1≤cos(a - b)≤1 ∴-1≤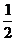 t2 -
t2 - ≤1
≤1
∴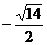 ≤t≤
≤t≤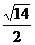
例5设a,bÎ(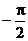 ,
,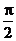 ),tana、tanb是一元二次方程
),tana、tanb是一元二次方程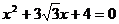 的两个根,求 a + b
的两个根,求 a + b
解:由韦达定理:
∴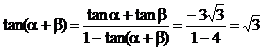
又由a,bÎ(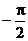 ,
,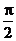 )且tana,tanb < 0 (∵tana+tanb<0,
tanatanb >0)
)且tana,tanb < 0 (∵tana+tanb<0,
tanatanb >0)
得a + bÎ (-p, 0) ∴a + b = 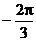
例6 已知sin(p - a) - cos(p + a) =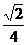 (0<a<p),求sin(p + a) + cos(2p - a)的值
(0<a<p),求sin(p + a) + cos(2p - a)的值
解:∵sin(p - a) - cos(p + a) =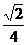 即:sin a + cos a =
即:sin a + cos a =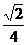 ①
①
又∵0<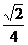 <1,0<a<p
<1,0<a<p 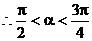 ∴sina>0, cosa<0
∴sina>0, cosa<0
令a = sin(p + a) + cos(2p - a) = - sina + cosa 则 a<0
由①得:2sinacosa = 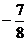
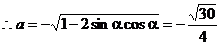
例7 已知2sin(p - a) - cos(p + a) = 1 (0<a<p),求cos(2p - a) + sin(p + a)的值
解:将已知条件化简得:2sin a + cos a = 1 ①
设cos(2p - a) + sin(p + a) = a , 则 a = cos a - sin a ②
①②联立得: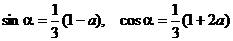
∵sin2a + cos2a =
1 ∴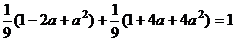
∴5a2 + 2a - 7 = 0,
解之得:a1 = 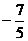 , a2 = 1(舍去)(否则sina = 0,
与0<a<p不符)
, a2 = 1(舍去)(否则sina = 0,
与0<a<p不符)
∴cos(2p - a) + sin(p + a) = 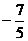
20.已知函数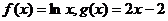 .
.
(1)试判断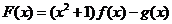 在
在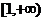 上的单调性;
上的单调性;
(2)当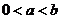 时,求证函数
时,求证函数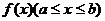 的值域的长度大于
的值域的长度大于 (闭区间[m,n]的长度定义为n-m).
(闭区间[m,n]的长度定义为n-m).
19.(1) 设函数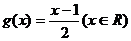 ,且数列
,且数列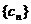 满足
满足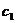 = 1,
= 1,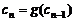 (n∈N,
(n∈N,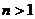 );求数列
);求数列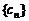 的通项公式.
的通项公式.
(2)设等差数列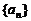 、
、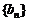 的前n项和分别为
的前n项和分别为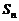 和
和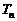 ,且
,且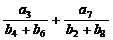
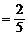 ,
,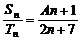 ,
,  ;求常数A的值及
;求常数A的值及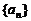 的通项公式.
的通项公式.
(3)若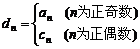 ,其中
,其中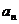 、
、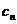 即为(1)、(2)中的数列
即为(1)、(2)中的数列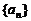 、
、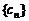 的第
的第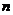 项,试求
项,试求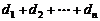 .
.
18.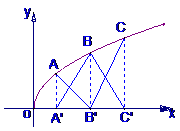 如图,点A、B、C都在幂函数
如图,点A、B、C都在幂函数 的图像上,它们的横坐标分别是a、a+1、a+2
的图像上,它们的横坐标分别是a、a+1、a+2  又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a)
又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a) 
(1)求函数f(a)和g(a)的表达式;
(2)比较f(a)与g(a)的大小,并证明你的结论 
17.某商店经销一种奥运纪念品,每件产品的成本为30元,并且每卖出一件产品需向税务部门上交 元(
元( 为常数,4<a≤5)的税收.设每件产品的日售价为x元(35≤x≤41),根据市场调查,日销售量与
为常数,4<a≤5)的税收.设每件产品的日售价为x元(35≤x≤41),根据市场调查,日销售量与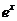 (e为自然对数的底数)成反比例.已知每件产品的日售价为40元时,日销售量为10件.
(e为自然对数的底数)成反比例.已知每件产品的日售价为40元时,日销售量为10件.
(1)求该商店的日利润L(x)元与每件产品的日售价x元的函数关系式;
(2)当每件产品的日售价为多少元时,该商品的日利润L(x)最大,并求出L(x)的最大值.
16.已知幂函数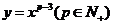 的图象关于y轴对称,且在
的图象关于y轴对称,且在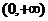 上是减函数,求满足
上是减函数,求满足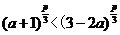 的a的取值范围.
的a的取值范围.
15.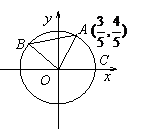 如图
如图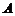 、
、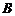 是单位圆
是单位圆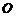 上的点,
上的点,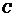 是圆
是圆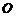 与
与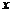 轴正半轴的交点,点
轴正半轴的交点,点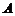 的坐标为
的坐标为 ,三角形
,三角形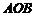 为直角三角形.
为直角三角形.
(1)求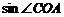 ,
,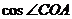 ;
;
(2)求线段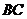 的长.
的长.
14.函数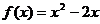 ,
,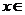
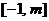 图象上的最高点为A,最低点为B,A、B两点之间的距离是
图象上的最高点为A,最低点为B,A、B两点之间的距离是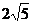 ,则实数
,则实数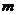 的取值范围是________________.
的取值范围是________________.
13.已知定义在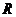 上的奇函数
上的奇函数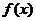 的图象关于直线
的图象关于直线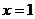 对称,
对称,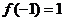 ,则
,则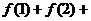
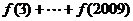 的值为________________.
的值为________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com