
2. (05北京卷)设f(x)是定义在[0, 1]上的函数,若存在x*∈(0,1),使得f(x)在[0, x*]上单调递增,在[x*,1]上单调递减,则称f(x)为[0, 1]上的单峰函数,x*为峰点,包含峰点的区间为含峰区间.对任意的[0,l]上的单峰函数f(x),下面研究缩短其含峰区间长度的方法.
(I)证明:对任意的x1,x2∈(0,1),x1<x2,若f(x1)≥f(x2),则(0,x2)为含峰区间;若f(x1)≤f(x2),则(x*,1)为含峰区间;
(II)对给定的r(0<r<0.5),证明:存在x1,x2∈(0,1),满足x2-x1≥2r,使得由(I)所确定的含峰区间的长度不大于 0.5+r;
(III)选取x1,x2∈(0, 1),x1<x2,由(I)可确定含峰区间为(0,x2)或(x1,1),在所得的含峰区间内选取x3,由x3与x1或x3与x2类似地可确定一个新的含峰区间.在第一次确定的含峰区间为(0,x2)的情况下,试确定x1,x2,x3的值,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0.34.(区间长度等于区间的右端点与左端点之差)
1、 (05广东卷)设函数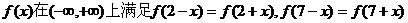 ,且在闭区间[0,7]上,只有
,且在闭区间[0,7]上,只有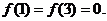 (Ⅰ)试判断函数
(Ⅰ)试判断函数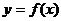 的奇偶性;
的奇偶性;
(Ⅱ)试求方程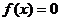 在闭区间[-2005,2005]上的根的个数,并证明你的结论.
在闭区间[-2005,2005]上的根的个数,并证明你的结论.
6.(05福建卷)把下面不完整的命题补充完整,并使之成为真命题.
若函数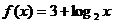 的图象与
的图象与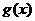 的图象关于
对称,则函数
的图象关于
对称,则函数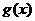 =
=
.
(注:填上你认为可以成为真命题的一种情形即可,不必考虑所有可能的情形)
5. (05北京卷)对于函数f(x)定义域中任意的x1,x2(x1≠x2),有如下结论:
①f(x1+x2)=f(x1)·f(x2);② f(x1·x2)=f(x1)+f(x2)③ >0;
>0;
④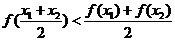 .当f(x)=lgx时,上述结论中正确结论的序号是
.当f(x)=lgx时,上述结论中正确结论的序号是
4.(05江苏卷)若3a=0.618,a∈ ,k∈Z,则k=
.
,k∈Z,则k=
.
3、(2005年高考·辽宁卷7)在R上定义运算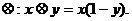 若不等式
若不等式
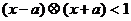 对任意实数
对任意实数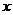 成立,
则 ( )
成立,
则 ( )
A.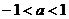 B.
B.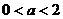 C.
C.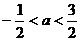 D.
D.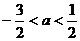
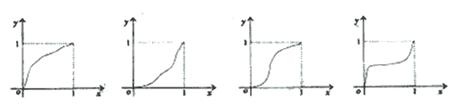
2. (辽宁卷)一给定函数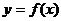 的图象在下列图中,并且对任意
的图象在下列图中,并且对任意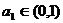 ,由关系式
,由关系式 得到的数列
得到的数列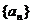 满足
满足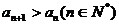 ,则该函数的图象是( )
,则该函数的图象是( )
1、(2005年高考·福建卷·理12)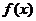 是定义在R上的以3为周期的奇函数,且
是定义在R上的以3为周期的奇函数,且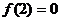 则方程
则方程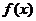 =0在区间(0,6)内解的个数的最小值是(错题!) ( )
=0在区间(0,6)内解的个数的最小值是(错题!) ( )
A.2 B.3 C.4 D.5
以近年高考对函数的考查为主,复习综合运用函数的知识、方法和思想解决问题.
12、函数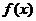 的定义域为R,且对任意
的定义域为R,且对任意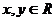 ,有
,有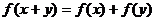 ,且当
,且当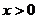 时,
时,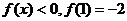 。
。
(1) 证明: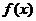 是奇函数;
是奇函数;
(2) 证明: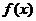 是R上的减函数;
是R上的减函数;
(3) 求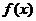 在区间
在区间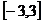 上的最大、最小值
上的最大、最小值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com