
2.我们南山区经过多年的初中课改,学生已经具备较强的自学能力,多数同学对数学的学习有相当的兴趣和积极性。
1.初中学生已经学习了基本的锐角三角函数的定义,掌握了锐角三角函数的一些常见的知识和求法。
10.(2006全国Ⅰ)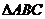 的三个内角为
的三个内角为 ,求当A为何值时,
,求当A为何值时, 取得最大值,并求出这个最大值
取得最大值,并求出这个最大值
解: 由A+B+C=π, 得 = - , 所以有cos =sin
cosA+2cos =cosA+2sin =1-2sin2 + 2sin
=-2(sin - )2+
当sin = , 即A=时, cosA+2cos取得最大值为
[探索题]是否存在锐角α、β,使①α+2β=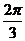 , ②
, ②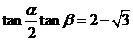 同时成立?若存在,求出α、β,若不存在,请说明理由.
同时成立?若存在,求出α、β,若不存在,请说明理由.
解:假设存在,由①得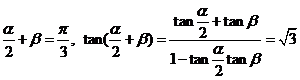
由②代入上式得 , 又②
, 又②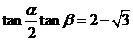
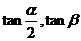 是方程
是方程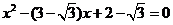 的两个根,解得
的两个根,解得
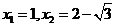 .
.
∵α、β是锐角, ∴ ,tanβ=1.
,tanβ=1.
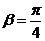 ,代入①得
,代入①得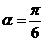 .即存在
.即存在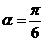 ,
,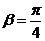 使①②式同时成立.
使①②式同时成立.
9. 求证:
证法1:左边=

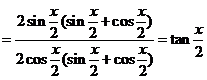
证法2:右边=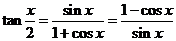
由合比定理得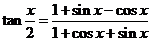
8.求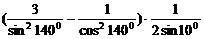 。
。
解:原式=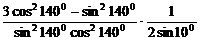
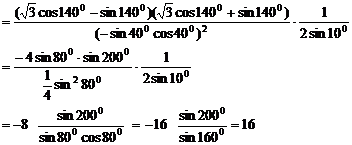
注:在化简三角函数式过程中,除利用三角变换公式,还需用到代数变形公式,如本题平方差公式。
7. 已知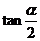 =2,求
=2,求
(I)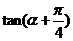 的值; (II)sin2α+sin2α+cos2α的值.
的值; (II)sin2α+sin2α+cos2α的值.
解:(I)∵
tan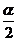 =2, ∴
=2, ∴ 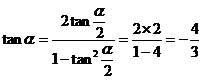 ;
;
所以 =
= ;
;
(II)sin2α+sin2α+cos2α=sin2α+sin2α+cos2α-sin2α
=2sinαcosα+cos2α
= =
=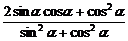
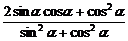 =
=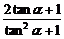 =1.
=1.
6.由已知得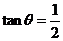 ,sin2θ-2cos2θ=
,sin2θ-2cos2θ=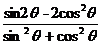 =
=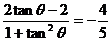
法二:sin2θ-2cos2θ=sin2θ-cos2θ-1=-cos(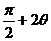 )-sin(
)-sin(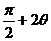 )-1
)-1
=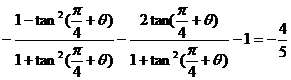
[解答题]
5.由已知得sinα=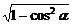 =
=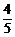 ,tan
,tan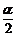 =
=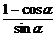 =
= .
.
法二:tan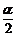 =
=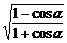 =
=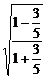 =
= .
.
6.已知tan(45°+θ)=3,则sin2θ-2cos2θ=_______
简答.提示:1-3. ABC;4. -
5. (2005春上海)若cosα=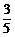 ,且α∈(0,
,且α∈(0,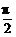 ),则tan
),则tan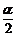 =_______
=_______
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com