
1、函数 的图象,可由
的图象,可由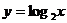 的图象
( )
的图象
( )
A、横坐标不变,纵坐标变为 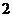 倍而得 B、纵坐标不变,横坐标变为 4倍而得
倍而得 B、纵坐标不变,横坐标变为 4倍而得
C、向上平移2个单位而得 D、向下平移2个单位而得
例1:(1)设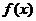 是定义域为R的任一函数,
是定义域为R的任一函数,
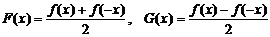 。
。
①判断 与
与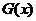 的奇偶性; ②试将函数
的奇偶性; ②试将函数 表示为一个奇函数与一个偶函数的和
表示为一个奇函数与一个偶函数的和
例2:定义在实数集上的函数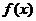 ,对任意
,对任意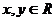 ,有
,有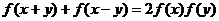 且
且 。
。
(1) 求证: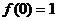
(2)判断 的奇偶性
的奇偶性
(3)若存在正数C,使 ,①求证对任意
,①求证对任意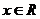 ,有
,有 成立
成立
②试问函数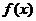 是不是周期函数。如果是,找出它的一个周期;如果不是请证明。
是不是周期函数。如果是,找出它的一个周期;如果不是请证明。
例3:已知函数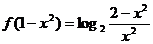
(1) 求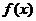 的解析式和定义域
的解析式和定义域
(2) 设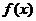 的反函数是
的反函数是 。求证:当
。求证:当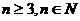 时,
时,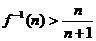 成立
成立
例4:已知奇函数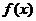 的定义域为R,且
的定义域为R,且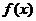 在
在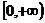 上增函数。当
上增函数。当 时,是否存在这样的实数
时,是否存在这样的实数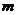 ,使
,使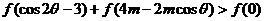 对所有
对所有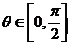 均成立?若存在,求所有适合条件的实数
均成立?若存在,求所有适合条件的实数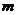 ,若存在,说明理由。
,若存在,说明理由。
4、若存在常数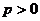 ,使得函数
,使得函数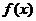 满足
满足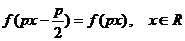 ,则
,则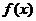 的一个正周期为
的一个正周期为
3、函数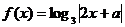 的对称轴为
的对称轴为 ,则
,则
2、定义在区间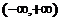 的奇函数
的奇函数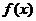 的增函数,偶函数
的增函数,偶函数 在区间
在区间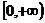 的图象与
的图象与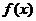 的图象重合。设
的图象重合。设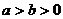 ,给出下列不等式,其中成立的是
( )
,给出下列不等式,其中成立的是
( )
(1) (2)
(2)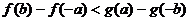
(3) (4)
(4)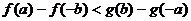
(A)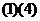 (B)
(B)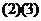 (C)
(C)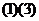 (D)
(D)
1、不等式 成立的一个充分不必要条件是 ( )
成立的一个充分不必要条件是 ( )
(A)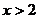 (B)
(B)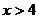 (C)
(C)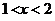 (D)
(D)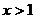
3、函数与解析几何知识结合的问题
在解决函数综合问题时,要进行等价转化、分类讨论、数形结合思想的综合运用
2、函数与其它代数知识,主要是方程、不等式、数列的综合问题;
函数思想是高中数学的主线,函数知识贯穿高中代数始终,函数知识是高中数学最重要的内容。函数综合问题主要表现在以下几个方面:
1、函数的概念、性质和方法的综合问题;
8、某工厂拟建一座平面图(如图所示)为矩形且面积为200平方米的三级污水处理池,由于地形限制,长、宽都不能超过16米,如果池外周壁建造单价为每米400元,中间池壁造价为每米248元,池底建造单价为每平方米80元。(池壁的厚度忽略不计,且池无盖)
(1) 写出总造价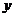 (元)与污水处理池长
(元)与污水处理池长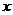 (米)的函数关系式,并指出定义域。
(米)的函数关系式,并指出定义域。
(2) 求污水处理池的长和宽各为多少时,污水处理池的总造价最低?并求出最低总造价?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com