
3、已知h>0,设命题甲:两个实数a,b满足|a-b|<2h;命题乙:两个实数a,b满足|a-c|<h且|b-c|<h,那么甲是乙成立的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
2、已知实数a,b满足ab<0,则( )
A.|a+b|>|a-b| B.|a+b|<|a-b| C.|a-b|<||a|-|b|| D.|a-b|<|a|+|b|
1、若a,b,c∈R,且|a-c|<|b|,则正确的是( )
A.|a|>|b|+|c| B.|a|<|b|-|c| C.|a|<|b|+|c| D.|a|>|c|-|b|
例1、△ABC中,求证: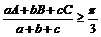 .
.
例2、已知a,b∈R,求证: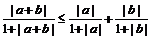 .
.
例3、设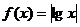 ,
, 满足
满足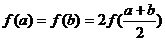 其中
其中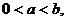 求证:
求证:
⑴ 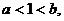 ⑵
⑵ 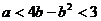
例4. 已知a,b,c∈R,函数f(x)=ax2+bx+c,g(x)=ax+b,当-1≤x≤1时,|f(x)|≤1,求证:①|c|≤1 ②当-1≤x≤1时,|g(x)|≤2.
例5.已知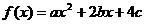 ,
,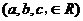
⑴若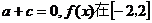 上的最大值为
上的最大值为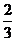 ,最小值为
,最小值为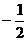 ,求证:
,求证: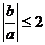
⑵当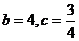 时,对于给定的负数
时,对于给定的负数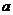 ,有一个最大的正数M
,有一个最大的正数M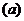 使得
使得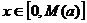 时,都有
时,都有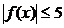 问
问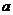 为何值时,
为何值时,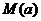 最大,并求出最大值
最大,并求出最大值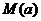 ,证明你的结论
,证明你的结论
5.已知|a|≠|b|,m= ,那么m、n之间的大小关系为 ( )
,那么m、n之间的大小关系为 ( )
A.m>n B.m<n C.m=n D.m≤n
4.不等式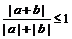 成立的充要条件是 ( )
成立的充要条件是 ( )
A.ab≠0 B.a2+b2≠0 C.ab>0 D.ab<0
2.ab>0,则①|a+b|>|a| ②|a+b|<|b| ③|a+b|<|a-b| ④|a+b|>|a-b|四个式中正确的是 ( )
A.①② B.②③ C.①④ D.②④
1.设x<3则下列不等式一定成立的是 ( )
A.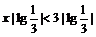 B.
B. C.
C. D.
D.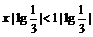
2、证明绝对值不等式主要有两种方法:
A)去掉绝对值符号转化为一般的不等式证明:换元法、讨论法、平方法;
B)利用不等式: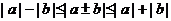 ,用这个方法要对绝对值内的式子进行分拆组合、添项减项、使要证的式子与已知的式子联系起来
,用这个方法要对绝对值内的式子进行分拆组合、添项减项、使要证的式子与已知的式子联系起来
1、解绝对值不等式必须设法化去式中的绝对值符号,转化为一般代数式类型来解;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com