
2、教学中学生通过观看动画、动手实践,自己总结出椭圆定义,符合从感性上升为理性的认识规律。
1、这节课围绕“认识椭圆→画椭圆→定义椭圆→推导椭圆方程→椭圆方程知识讲解→椭圆方程知识运用”这一主线展开。
教学流程设计:认识椭圆→画椭圆→定义椭圆→推导椭圆方程→椭圆方程知识讲解→椭圆方程知识运用→本课小结→作业布置
|
教 学 环 节 |
教学程序(师生双边活动) |
设计意图 |
|
|
认 识 椭 圆 |
图片展示:椭圆就在我们身边。
|
(1)、从学生所关心的实际问题引入,使学生了解数学来源于实际。 (2)、展示图片,使学生更好的掌握椭圆形状,更直观、形象地了解后面要学的内容; |
|
|
画 椭 圆 |
1、画一画 (画椭圆): (1)、请学生拿出课前准备的硬纸板、细线、铅笔,同桌一起合作画椭圆。 (2)、 3、椭圆画法:(1)画圆;(2)画椭圆。(可叫四位同学一组,自备细绳,现场画图;教师展示课件:椭圆的形成。) 课件动态演示椭圆的形成过程: 接着指出:这就是我们要学习的一类新的封闭曲线--椭圆。 |
(1)、通过画图给学生提供一个动手操作、合作学习的机会;调动学生学习的积极性 (2)、多媒体演示向学生说明椭圆的具体画法,更直观形象。 |
|
|
定 义 椭 圆 |
2、议一议(椭圆的定义及有关概念) (1)、由学生画图及教师演示椭圆的形成过程,引导学生归纳定义。 定义:在平面内,到两定点F1,F2的距离之和等于常数2a(2a>∣F1F2 |)的点的轨迹叫做椭圆。 这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距,记∣F1F2 |=2c. (2)、椭圆定义的再认识。 问题:为什么要满足2a>2c呢?(1)当2a=2c时,轨迹是什么?(2)当2a<2c时,轨迹又是什么? 结论:(1)、当2a>|F1F2|时,是椭圆; (2)、当2a=|F1F2|时,是线段; (3)、当2a<|F1F2|轨迹不存在。 |
让学生通过反思画图,归纳定义,理解定义,利用动画演示,深刻地理解椭圆定义条件,突破了重点。 |
|
|
推 导 椭 圆 方 程 |
3、求一求:(椭圆标准方程的推导) (教师引导)设问1:求曲线方程的一般方法样?(建系、设点、列式、化简) 设问2:本题中可以怎样建立直角坐标系?(让学生根据自已的经验来确定) 方案1:(如图1)以F1、F2所在的直线为 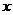 轴,F1F2的中点为原点建立直角坐标系: 轴,F1F2的中点为原点建立直角坐标系:
方案2:(如图2)以F1、F2所在的直线为 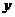 轴, 轴,
|
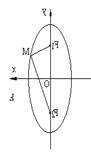
图1 图2
方程: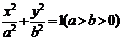 和
和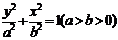
请学生观察归纳二个方程的特征,从而区别焦点在不同坐标轴上的椭圆标方程;令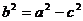 要渗透数学对称美教学。
要渗透数学对称美教学。
说明:①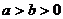 ;
;
②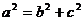 (要区别与习惯思维下的勾股定理
(要区别与习惯思维下的勾股定理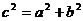 );
);
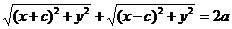 但不会化简。
但不会化简。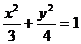 (2)
(2)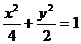
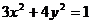 (4)
(4)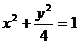
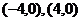 ,椭圆上一点P到两焦点距离的和等于10
,椭圆上一点P到两焦点距离的和等于10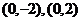 ,并且椭圆经过点
,并且椭圆经过点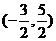
 的两个焦点,过F1的直线交椭圆于M、N两点,则
的两个焦点,过F1的直线交椭圆于M、N两点,则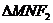 的周长为
。
的周长为
。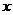 轴、
轴、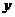 轴的上的两个标准方程)、
轴的上的两个标准方程)、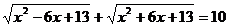
“授人以鱼,不如授人以渔.” 教会学生:
1、动手尝试;2、仔细观察;3分析讨论;4、抽象出概念,推出方程。这样有利于学生发挥学习的主动性,使学生的学习过程成为在教师引导下的“再创造”过程.
2、探索讨论法:由学生通过联想、归纳把原有的求轨迹方法迁移到新情况中,有利于学生对知识进行主动建构;
有利于突出重点,突破难点,发挥其创造性。
引导发现法和探索讨论法是适应新课程体系的一种全新教学模式,它能更好地体现学生的主体性,实现师生、生生交流,体现课堂的开放性与公平性。
教学手段:利用多媒体课件教学,化抽象为具体,降底学生学习难度,增强动感及直观感,增大教学容量,提高教学质量。
课堂教学中创设问题的情境,激发学生主动的发现问题解决问题,充分调动学生学习的主动性、积极性;有效地渗透数学思想方法,发展学生个性思维品质,这是本节课的教学原则 。根据这样的原则及所要完成的教学目标 ,我采用如下的教学方法和手段:
教学方法:我采用的是引导发现法、探索讨论法等。
1、引导发现法:用课件演示动点的轨迹,启发学生归纳、概括椭圆定义。
4、教材处理
根据新大纲要求,本节课的内容特点以及结合我校学生的实际情况,我把本节内容分2个课时进行教学。
第一课时,主要研究椭圆的定义、标准方程的推导。
第二课时,运用椭圆的定义求曲线的轨迹方程。
3、教学重点、难点
教学重点:椭圆的定义及椭圆的标准方程
教学难点:椭圆标准方程的建立和推导。
在学习本课《椭圆及其标准方程》前,学生已学习了直线与圆的方程,对曲线和方程的概念有了一些了解与运用的经验,用坐标法研究几何问题也有了初步的认识。但由于学生学习解析几何时间还不长、学习程度也较浅,学生对坐标法解决几何问题掌握还不够。另外,学生对含有两个根式之和(差)等式化简的运算生疏,去根式的策略选择不当等是导致“标准方程的推导”成为学习难点的直接原因。
据以上对教材及学情的分析,确定椭圆的定义及其标准方程为本课的教学重点;椭圆标准方程的推导为本课的难点。
2、教学目标
根据上述教材结构与内容分析,考虑到学生已有的认知结构心理特征,制定如下教学目标:
(1)、知识目标:掌握椭圆的定义及其标准方程,通过对椭圆标准方程的探求,熟悉求曲线方程的一般方法。
(2)、能力目标:让学生通过自我探究、操作、数学思想(待定系数法)的运用等,从而提高学生实际动手、合作学习以及运用知识解决实际问题的能力。
(3)、情感目标:在教学中充分揭示“数”与“形”的内在联系,体会形数美的统一,激发学生学习数学的兴趣,培养学生勇于探索,勇于创新的精神。
1、教材的地位及作用
江苏教育版(选修2-1)第二章《圆锥曲线》是高考重点考查章节。“椭圆及其标准方程”是《圆锥曲线》第一节的内容,是继学习圆以后运用 “曲线和方程”理论解决具体的二次曲线的又一实例。从知识上说,它是运用坐标法研究曲线的几何性质的又一次实际演练,同时它也是进一步研究椭圆几何性质的基础;从方法上说,它为后面研究双曲线、抛物线提供了基本模式和理论基础;所以说,无论从教材内容,还是从教学方法上都是起着承上启下的作用,它是学好本章内容的关键。因此搞好这一节的教学,具有非常重要的意义。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com