
2.底数相同的指数函数和对数函数互为反函数,它们的图象关于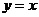 对称,它们在各自的定义域内增减性是一致的,通过函数图象,利用数形结合,记作指数函数与对数函数的性质.
对称,它们在各自的定义域内增减性是一致的,通过函数图象,利用数形结合,记作指数函数与对数函数的性质.
作业:P90 A组 3 7
P91 B组 3 4
第三章 函数的应用
1.指数与对数实质上只是同一数量关系的两种不同的形式,它们之间可以互化,这种等价互化也是指数运算和对数运算的常用方法.
2.指数函数与对数函数
问题1:函数 分别必须满足什么条件.
分别必须满足什么条件.
问题2:在同一直角坐标系中画出函数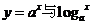 的图象,并说明两者之间的关系.
的图象,并说明两者之间的关系.
问题3:根据图象说出指数函数与对数函数的性质.
例2:已知函数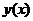 的图象沿
的图象沿 轴方向向左平移1个单位后与
轴方向向左平移1个单位后与 的图象关于直线
的图象关于直线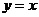 对称,且
对称,且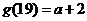 ,则函数
,则函数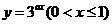 的值域为
.
的值域为
.
分析:函数 关于直线
关于直线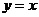 对称的函数为
对称的函数为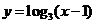
∴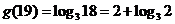
∴
∵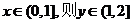
小结:底数相同的指数函数与对数函数关于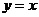 对称,它们之间还有一个关系式子:
对称,它们之间还有一个关系式子: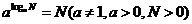
例3:已知
(1)求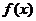 的定义域
的定义域
(2)求使 的
的 的取值范围
的取值范围
分析:(1)要求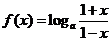 的定义域,
的定义域,
则应有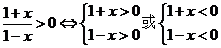
(2)注意考虑不等号右边的0化为 ,则(2)小题变为
,则(2)小题变为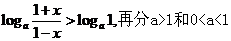 两种情况分别求出
两种情况分别求出 .
.
建议:通过提问由学生作答
课堂小结:
2、指数与对数
指数式与对数式的互化
 幂值 真数
幂值 真数



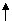

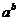 = N
= N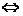
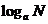 = b
= b

底数

指数←→对数值
提问:在对数式中,a,N,b的取值范围是什么?
例1:已知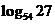 =
= ,54b=3,用
,54b=3,用 的值
的值
解法1:由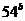 =3得
=3得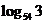 =b
=b
∴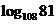 =
= =
=
解法2:由
设
所以
即:
所以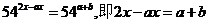
因此得: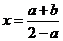
(1)法1是通过指数化成对数,再由对数的运算性质和换底公式计算结果.
法2是通过对数化成指数,再由指数的运算性质计算出结果,但法2运算的技巧性较大。
1、回顾本章的知识结构

2、教具:投影仪。
1、学法:讲授法、讨论法。
重点:指数函数与对数函数的性质。
难点:灵活运用函数性质解决有关问题。
3.情感、态度、价值观
(1)提高学生的认知水平,为学生塑造良好的数学认识结构.
(2)培养学生数形结合的思想观念及抽象思维能力.
2.过程与方法
通过提问,分析点评,让学生更能熟悉指数函数,对数函数的性质.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com