
科目: 来源: 题型:
【题目】(问题背景)
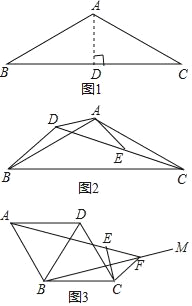
如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°,
∠BAC=60°,![]() .
.
(问题应用)
如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D、E、C三点共线,连接BD,
(1)求证:△ADB≌△AEC;
(2)直接写出AD、BD、CD之间的数量关系;
如图3,菱形ABCD中,∠ABC=120°,在△ABC内部作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE、CF.
(1)判断△EFC的形状,并给出证明.
(2)若AE=5,CE=2,求BF的长.
查看答案和解析>>
科目: 来源: 题型:
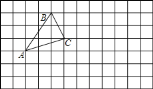
【题目】画图并填空:(每个小方格的边长为1)
(1)画出△ABC先向右平移6格,再向下平移2格得到的△A1B1C1.
(2)线段AA1与线段BB1的关系是: .
(3)△ABC的面积是 .
查看答案和解析>>
科目: 来源: 题型:
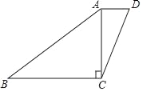
【题目】如图,一张四边形纸片ABCD,AB=20,BC=16,CD=13,AD=5,对角线AC⊥BC.
(1)求AC的长;
(2)求四边形纸片ABCD的面积;
(3)若将四边形纸片ABCD沿AC剪开,拼成一个与四边形纸片ABCD面积相等的三角形,直接写出拼得的三角形各边高的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列关于分式的判断,正确的是( )
A.当x=2时, ![]() 的值为零
的值为零
B.无论x为何值, ![]() 的值总为正数
的值总为正数
C.无论x为何值, ![]() 不可能得整数值
不可能得整数值
D.当x≠3时, ![]() 有意义
有意义
查看答案和解析>>
科目: 来源: 题型:
【题目】[感知]
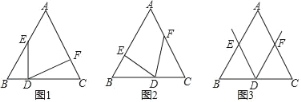
如图①,△ABC是等边三角形,D是边BC上一点(点D不与点B、C重合),作∠EDF=60°,使角的两边分别交边AB、AC于点E、F,且BD=CF.若DE⊥BC,则∠DFC的大小是 度;
[探究]
如图②,△ABC是等边三角形,D是边BC上一点(点D不与点B、C重合),作∠EDF=60°,使角的两边分别交边AB、AC于点E、F,且BD=CF.求证:BE=CD;
[应用]
在图③中,若D是边BC的中点,且AB=2,其它条件不变,如图③所示,则四边形AEDF的周长为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x、y的方程组![]() ,其中﹣3≤a≤1,给出下列结论:
,其中﹣3≤a≤1,给出下列结论:
①![]() 是方程组的解;
是方程组的解;
②当a=﹣2时,x+y=0;
③若y≤1,则1≤x≤4;
④若S=3x﹣y+2a,则S的最大值为11.
其中正确的有_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数。
解:∵EF∥AD,
∴∠2= ( )
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=70°,∴∠AGD= 。

查看答案和解析>>
科目: 来源: 题型:
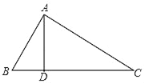
【题目】题目:如图,在△ABC中,点D是BC边上一点,连结AD,若AB=10,AC=17,BD=6,AD=8,解答下列问题:
(1)求∠ADB的度数;
(2)求BC的长.
小强做第(1)题的步骤如下:∵AB2=BD2+AD2
∴△ABD是直角三角形,∠ADB=90°.
(1)小强解答第(1)题的过程是否完整,如果不完整,请写出第(1)题完整的解答过程
(2)完成第(2)题.
查看答案和解析>>
科目: 来源: 题型:
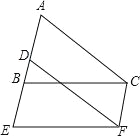
【题目】如图,将△ABC沿射线AB的方向平移2个单位到△DEF的位置,点A、B、C的对应点分别点D、E、F.
(1)直接写出图中与AD相等的线段.
(2)若AB=3,则AE=______.
(3)若∠ABC=75°,求∠CFE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com