
科目: 来源: 题型:
【题目】“六一”前夕,某玩具经销商用去2350元购进A、B、C三种新型的电动玩具共50套,并且购进的三种玩具都不少于10套,设购进A种玩具x套,B种玩具y套,三种电动玩具的进价和售价如表所示
型 号 | A | B | C |
进价(元/套) | 40 | 55 | 50 |
售价(元/套) | 50 | 80 | 65 |
(1)用含x、y的代数式表示购进C种玩具的套数;
(2)求y与x之间的函数关系式;
(3)假设所购进的这三种玩具能全部卖出,且在购销这种玩具的过程中需要另外支出各种费用200元.
①求出利润P(元)与x(套)之间的函数关系式;②求出利润的最大值,并写出此时三种玩具各多少套.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好.
(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2,并指出她与嘉嘉抽到勾股数的可能性一样吗?

查看答案和解析>>
科目: 来源: 题型:
【题目】小亮妈妈下岗后开了一家糕点店,现有10.2千克面粉,10.2千克鸡蛋,计划加工一般糕点和精制糕点两种产品共50盒.

⑴有哪几种符合题意的加工方案?请你帮忙设计出来;
⑵若销售一般糕点和精制糕点的利润分别为1.5元/盒和2元/盒,试问哪种方案使小亮妈妈可获得最大利润?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】四张质地、大小、背面完全相同的卡片上,正面分别画有平行四边形、矩形、等腰三角形、菱形四个图案.现把它们的正面向下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案是中心对称图形的概率为___________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】.如图①,ABC中,沿BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿B1A1C的平分线A1B2折叠,剪掉重叠部分;……将余下部分沿BnAnC(n为正整数)的平分线AnBn1折叠,点Bn与点C重合.无论折叠多少次,只要最后一次点Bn与点C恰好重合,我们就称BAC是ABC的好角.
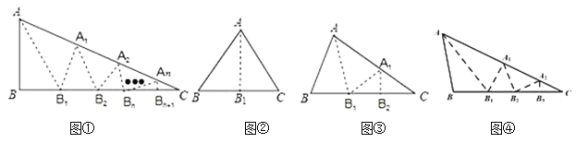
小丽展示了确定BAC是ABC的好角的两种情形.
情形一:如图②,沿等腰三角形ABC顶角BAC是平分线AB1折叠,点B与点C重合;
情形二:如图③,沿ABC的BAC的平分线AB1折叠,剪掉重叠部分;将余下的部分沿B1A1C的平分线A1B2折叠,此时点B1与点C重合.
(探究发现)
⑴如图③,ABC中,B2C,经过两次折叠,BAC是不是ABC的好角? .(填:“是”或“不是”)
⑵归纳猜想:(i)如图④,小丽经过三次折叠发现了BAC是ABC的好角,请探究B与C(BC)之间的等量关系,并说明理由.
(ii)根据以上内容猜想:若经过n(n为正整数)次折叠BAC是ABC的好角,则B与C(BC)之间的等量关系为 .(直接写出结论)
⑶小丽找到一个三角形,三个角分别为15,60,105,发现60和105的两个角都是此三角形的好角,请你完成,如果一个三角形的最小角是10,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD边长为4,点P从点A运动到点B,速度为1,点Q沿B﹣C﹣D运动,速度为2,点P、Q同时出发,则△BPQ的面积y与运动时间t(t≤4)的函数图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.
(1)求二次函数的解析式;
(2)点P在x轴正半轴上,且PA=PC,求OP的长;
(3)点M在二次函数图象上,以M为圆心的圆与直线AC相切,切点为H.
①若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标;
②若⊙M的半径为![]() ,求点M的坐标.
,求点M的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】在ABCD中,点P和点Q是直线BD上不重合的两个动点,AP∥CQ,AD=BD.
(1)如图①,求证:BP+BQ=BC;
(2)请直接写出图②,图③中BP、BQ、BC三者之间的数量关系,不需要证明;
(3)在(1)和(2)的条件下,若DQ=2,DP=6,则BC= .

查看答案和解析>>
科目: 来源: 题型:
【题目】已知ABC在平面直角坐标系内,满足:点A在y轴正半轴上移动,点B在x轴负半轴上移动,点C为y轴右侧一动点.

点A0,a和点Bb,0坐标恰好满足:![]() ,直接写出a,b的值.
,直接写出a,b的值.
⑵如图①,当点C在第四象限时,若AM、AO将BAC三等分,BM、BO将ABC三等分,在A、B、C的运动过程中,试求出C和M的关系.
⑶探究:
(i)如图②,当点C在第四象限时,若AM平分CAO,BM平分CBO,在A、B、C的运动过程中,C和M是否存在确定的数量关系?若存在,请证明你的结论;若不存在,请说明理由.
(ii)如图③,当点C在第一象限时,且在(i)中的条件不变的前提下,C和M又有何数量关系?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com