
科目: 来源: 题型:
【题目】如图,长方形ABCD中,AB=3,BC=4,点E是BC边上任一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当CE的长为_____时,△CEB′恰好为直角三角形.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,小刚将一个正方形纸片剪去一个宽为5cm的长条后,再从剩下的长方形纸片上剪去一个宽为6cm的长条,如果两次剪下的长条面积正好相等,求两个所剪下的长条的面积之和为( )

A.215cm2B.250cm2C.300cm2D.320cm2
查看答案和解析>>
科目: 来源: 题型:
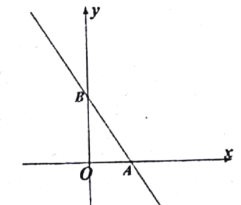
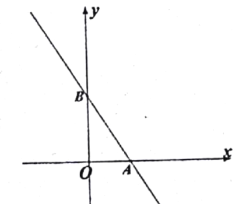
【题目】如图,在直角坐标系中,已知直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值及
的值及![]() 的面积;
的面积;
(2)点![]() 在
在![]() 轴上,若
轴上,若![]() 是以
是以![]() 为腰的等腰三角形,直接写出点
为腰的等腰三角形,直接写出点![]() 的坐标;
的坐标;
(3)点![]() 在
在![]() 轴上,若点
轴上,若点![]() 是直线
是直线![]() 上的一个动点,当
上的一个动点,当![]() 的面积与
的面积与![]() 的面积相等时,求点
的面积相等时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
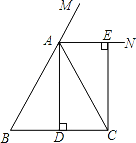
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目: 来源: 题型:
【题目】为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,如图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题:
(1)求手机支付金额y(元)与骑行时间x(时)的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,若四边形AODE是平行四边形,求点D的坐标.
(3)P是抛物线上的第一象限内的动点,过点P作PM⊥x轴,垂足是M,是否存在点p,使得以P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
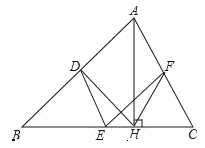
【题目】如图,在△ABC中,点D、E、F分别是边AB、BC、CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)若∠AHF=20°,∠AHD=50°,求∠DEF的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=-x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D,C关于抛物线的对称轴对称,直线AD与y轴相交于点E.
(1)求直线AD的解析式;
(2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH周长的最大值;
(3)如图2,点M是抛物线的顶点,点P是y轴上一动点,点Q是坐标平面内一点,四边形APQM是以PM为对角线的平行四边形,点Q′与点Q关于直线AM对称,连接M Q′,P Q′.当△PM Q′与□APQM重合部分的面积是□APQM面积的![]() 时,求□APQM面积.
时,求□APQM面积.

查看答案和解析>>
科目: 来源: 题型:
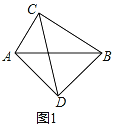
【题目】问题背景:如图(1)在四边形ABCD中,∠ACB=∠ADB=90°,AD=BD,探究线段AC、BC、CD之间的数量关系.小明探究此问题的思路是:将△BCD绕点D逆时针旋转90°到△AED处,点B、C分别落在点A、E处(如图(2)),易证点C、A、E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC=![]() CD.
CD.
简单应用:
(1)在图(1)中,若AC=![]() ,BC=2
,BC=2![]() ,求CD的长;
,求CD的长;
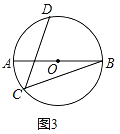
(2)如图(3)AB是⊙O的直径,点C、D在⊙O上,AD=BD,若AB=13,BC=12,求CD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com