
科目: 来源: 题型:
【题目】下列函数关系中,可以看做二次函数y=a![]() +bx+c模型的是( )
+bx+c模型的是( )
A. 在一定距离内,汽车行驶的速度与行驶的时间的关系
B. 我国人中自然增长率为1%,这样我国总人口数随年份变化的关系
C. 竖直向上发射的信号弹,从发射到落回地面,信号弹的高度与时间的关系(不计空气阻力)
D. 圆的周长与半径之间的关系
查看答案和解析>>
科目: 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】将连续的奇数1,3,5,7,9……,排成如图的数表:

(1)十字框的5个数的和与中间的数23有什么关系,若将十字框上下左右平移,可框住另外5个数,这5个数还有这种规律吗.
(2)设十字框中中间的数为![]() ,用含
,用含![]() 的式子表示十字框中的5个数之和.
的式子表示十字框中的5个数之和.
(3)十字框中的5个数的和能等于1045吗.若能,请写出这5个数,若不能,说明理由.
查看答案和解析>>
科目: 来源: 题型:
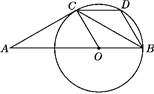
【题目】如图,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一点O,使OB=OC,以点O为圆心,OB为半径作圆,过点C作CD∥AB交⊙O于点D,连接BD.
(1)猜想AC与⊙O的位置关系,并证明你的猜想;
(2)试判断四边形BOCD的形状,并证明你的判断;
(3)已知AC=6,求扇形OBC所围成的圆锥的底面圆的半径r.
查看答案和解析>>
科目: 来源: 题型:
【题目】南果梨是东北辽宁省的一大特产,现有20筐南国梨,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值 (单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐南果梨中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐南果梨总计超过或不足多少千克?
(3)若南果梨每千克售价4元,则这20筐可卖多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知A(﹣4,2)、B(n,﹣4)是一次函数y=kx+b的图象与反比例函数y=![]() 的图象的两个交点;
的图象的两个交点;
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】为鼓励居民节约用电,某市采用价格调控手段达到省电目的.该市电费收费标准如下表(按月结算) :
每月用电量/度 | 电价/(元/度) |
不超过 |
|
超过 |
|
超过 |
|
解答下列问题:
(1)某居民![]() 月份用电量为
月份用电量为![]() 度,请问该居民
度,请问该居民![]() 月应缴电费多少元?
月应缴电费多少元?
(2)设某月的用电量为![]() 度
度![]() ,试写出不同用电量范围应缴的电费(用
,试写出不同用电量范围应缴的电费(用![]() 表示) .
表示) .
(3)某居民![]() 月份缴电费
月份缴电费![]() 元,求该居民
元,求该居民![]() 月份的用电量.
月份的用电量.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,y关于x的函数关系式为 ,自变量x的取值范为 ;药物燃烧后,y关于x的函数关系式为 .
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过 分钟后,员工才能回到办公室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
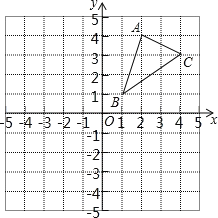
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).
(4)在x轴上有一点P,PA+PB的值最小,请直接写出点P的坐标
查看答案和解析>>
科目: 来源: 题型:
【题目】《庄子·天下》:“一尺之棰,日取其半,万世不竭.”意思是说:一尺长的木棍,每天截掉一半,永远也截不完.我国智慧的古代人在两千多年前就有了数学极限思想,今天我们运用此数学思想研究下列问题.
(规律探索)
(1)如图1所示的是边长为1的正方形,将它剪掉一半,则S阴影1=1-![]() =__________;
=__________;
如图2,在图1的基础上,将阴影部分再裁剪掉—半,则S阴影2=1-![]() -(
-(![]() )2=_______;
)2=_______;
同种操作,如图3,S阴影3=1-![]() -(
-(![]() )2-(
)2-(![]() )3=__________;
)3=__________;
如图4,S阴影4=1-![]() -(
-(![]() )2-(
)2-(![]() )3-(
)3-(![]() )4=___________;
)4=___________;
……
若同种地操作n次,则S阴影n=1-![]() -(
-(![]() )2-(
)2-(![]() )3-…-(
)3-…-(![]() )n=_________.
)n=_________.
(规律归纳)
(2)直接写出![]() +
+![]() +
+![]() +…+
+…+![]() 的化简结果:_________.
的化简结果:_________.
(规律应用)
(3)直接写出算式![]() +
+![]() +
+![]() +…+
+…+![]() 的值:__________.
的值:__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com