
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2+6mx+n(m>0)与x轴交于A,B两点(点A在点B左侧),顶点为C,抛物线与y轴交于点D,直线BC交y轴于E,S△ABC:S△AEC = 2∶3.
(1)求点A的坐标;
(2)将△ACO绕点C顺时针旋转一定角度后,点A与B重合,此时点O恰好也在y轴上,求抛物线的解析式.
查看答案和解析>>
科目: 来源: 题型:
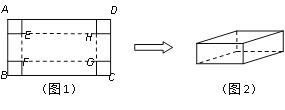
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,如图1,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面为矩形EFGH,如图2.设小正方形的边长为x厘米.
(1)当矩形纸板ABCD的一边长为90厘米时,求纸盒的侧面积的最大值;
(2)当EH:EF=7:2,且侧面积与底面积之比为9:7时,求x的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 和直线
和直线![]() (
(![]() 不同时为0),则点
不同时为0),则点![]() 到直线
到直线![]() 的距离
的距离![]() 可用公式
可用公式![]() 计算.
计算.
例如.求点![]() 到直线
到直线![]() 的距离.
的距离.
解:由直线可知![]()
∴![]()
根据以上材料,解答下列问题:
(1) 求点![]() 到直线
到直线![]() 的距离;
的距离;
(2) 求点![]() 到直线
到直线![]() 的距离,并说明点
的距离,并说明点![]() 与直线的位置关系;
与直线的位置关系;
(3)已知直线![]() 与直线
与直线![]() 平行,求两条平行线间的距离.
平行,求两条平行线间的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】6张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
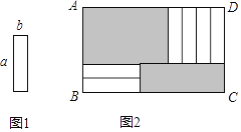
A. a=2b B. a=3b C. a=4b D. a=b
查看答案和解析>>
科目: 来源: 题型:
【题目】某校举行猜谜语大赛,甲、乙两队各有5名选手参赛。他们的成绩(满分100分,两个1号队员的成绩均未统计)如图所示

成绩统计分析表:
平均数 | 中位数 | 众数 | 方差 | 优秀率 | |
甲队 | 85 | 85 | 70 | 80% | |
乙队 | 85 | 160 |
根据以上材料
(1)计算出甲、乙两队1号选手的成绩;
(2)补充完成成绩统计图和成绩统计分析表.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司开发生产960件新产品,需要加工后才能投放市场,现甲、乙两个工厂都想加工这批产品,已知甲工厂单独完成这批产品比乙工厂单独完成这批产品多用20天,而乙工厂每天加工的件数是甲工厂每天加工件数的1.5倍,公司需付甲工厂加工费每天80元,乙工厂每天加工费用120元。
(1)求甲、乙两个工厂每天各能加工多少个新产品?
(2)公司制定产品加工方案如下:可以由每个厂家单独完成,也可以由两个厂家同时合作完成。在加工过程中,公司派一名工程师每天来厂进行技术指导,并负担每天5元的午餐补助费,请你帮助公司选择一种既省时又省力的方案,并说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P、Q两点停止运动.
(1)AC=__cm,BC=__cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,PQ=1cm.
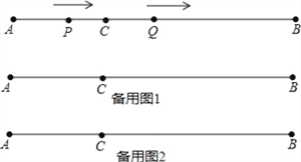

查看答案和解析>>
科目: 来源: 题型:
【题目】利用无刻度的直尺和圆规作出符合要求的图形.(注:不要求写作法,但保留作图痕迹)
(1)如图,已知线段AB,作一个△ABC,使得∠ACB=90°;(只需画一个即可)
(2)如图,已知线段MN,作一个△MPN,使得∠MPN=90°且sinM=![]() .(只需画一个即可)
.(只需画一个即可)

(1) (2)
查看答案和解析>>
科目: 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随时用的共享单车。某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费。具体收费标准如下:

同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:

(1)写出a、b的值。
(2)已知该校有5100名师生,且A品牌共享单车投放该校一天的费用为5800元。试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利?说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com