
科目: 来源: 题型:
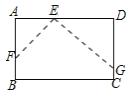
【题目】如图1,在长方形纸片ABCD中,E点在边AD上,F、G分别在边AB、CD上,分别以EF、EG为折痕进行折叠并压平,点A、D的对应点分别是点A′和点D′,若ED′平分∠FEG,且![]() 在
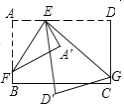
在![]() 内部,如图2,设∠A′ED'=n°,则∠FE D′的度数为___________(用含n的代数式表示).
内部,如图2,设∠A′ED'=n°,则∠FE D′的度数为___________(用含n的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】随着互联网的普及,某手机厂商采用先网络预定,然后根据订单量生产手机的方式销售,2015年该厂商将推出一款新手机,根据相关统计数据预测,定价为2200元,日预订量为20000台,若定价每减少100元,则日预订量增加10000台.
(1)设定价减少x元,预订量为y台,写出y与x的函数关系式;
(2)若每台手机的成本是1200元,求所获的利润w(元)与x(元)的函数关系式,并说明当定价为多少时所获利润最大;
(3)若手机加工厂每天最多加工50000台,且每批手机会有5%的故障率,通过计算说明每天最多接受的预订量为多少?按最大量接受预订时,每台售价多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】中小学生每天在校体育活动时间不低于1小时”![]() 为此,我区就“你每天在校体育活动时间是多少”的问题随机调查了区内300名初中学生
为此,我区就“你每天在校体育活动时间是多少”的问题随机调查了区内300名初中学生![]() 根据调查结果绘制成的统计图
根据调查结果绘制成的统计图![]() 部分
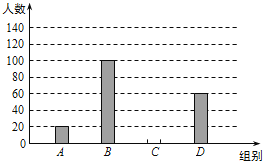
部分![]() 如图所示,其中分组情况是:
如图所示,其中分组情况是:
A组:![]() B组:
B组:![]() C组:
C组:![]() D组:
D组:![]()
请根据上述信息解答下列问题:
![]() 组的人数是______.
组的人数是______.
![]() 本次调查数据的中位数落在______组内;
本次调查数据的中位数落在______组内;
![]() 若我区有5400名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
若我区有5400名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:![]() ,且
,且![]() 、
、![]() 、
、![]() 分别是点A. B. C在数轴上对应的数.
分别是点A. B. C在数轴上对应的数.

(1)写出![]() =___;
=___;![]() =___;
=___;![]() =___.
=___.
(2)若甲、乙、丙三个动点分别从A.B.C三点同时出发沿数轴负方向运动,它们的速度分别是1、2、4,(单位/秒),运行![]() 秒后,甲、乙、丙三个动点对应的位置分别为:
秒后,甲、乙、丙三个动点对应的位置分别为:![]() ,
,![]() ,
,![]() ,当
,当![]() 时,求式子
时,求式子![]() 的值.
的值.
(3)若甲、乙、丙三个动点分别从A,B,C三点同时出发沿数轴正方向运动,它们的速度分别是1,2,4(单位/秒),运动多长时间后,乙与甲、丙等距离?
查看答案和解析>>
科目: 来源: 题型:
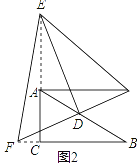
【题目】已知△ABC中,∠ACB=90°,D是AB的中点,∠EDF=90°
(1)如图1,若E、F分别在AC、BC边上,猜想AE2、BF2和EF2之间有何等量关系,并证明你的猜想;
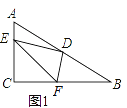
(2)若E、F分别在CA、BC的延长线上,请在图2中画出相应的图形,并判断(1)中的结论是否仍然成立(不作证明)
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)证明:“三角形内角和是180°”;
(2)请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题,判断这一逆命题是真命题还是假命题,如果是真命题给出证明,如果是假命题,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2 , 也可以表示为4×![]() ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 .
ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 .

(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,直角△ABC中,∠ACB=90°,AC=3cm,BC=4cm,则斜边AB上的高CD的长为多少?
(3)试构造一个图形,使它的面积能够解释(a+b)(a+2b)=a2+3ab+2b2 , 画在如图4的网格中,并标出字母a、b所表示的线段.
查看答案和解析>>
科目: 来源: 题型:
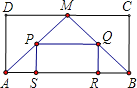
【题目】如图,在矩形ABCD中,M为CD的中点,连接AM、BM,分别取AM、BM的中点P、Q,以P、Q为顶点作第二个矩形PSRQ,使S、R在AB上![]() 在矩形PSRQ中,重复以上的步骤继续画图
在矩形PSRQ中,重复以上的步骤继续画图![]() 若
若![]() ,矩形ABCD的周长为
,矩形ABCD的周长为![]() 则:
则:![]() ______;
______;![]() 第n个矩形的边长分别是______.
第n个矩形的边长分别是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() .
.
(1)求证:抛物线与![]() 轴必定有公共点;
轴必定有公共点;
(2)若P(![]() ,y1),Q(-2,y2)是抛物线上的两点,且y1
,y1),Q(-2,y2)是抛物线上的两点,且y1![]() y2,求
y2,求![]() 的取值范围;
的取值范围;
(3)设抛物线与x轴交于点![]() 、
、![]() ,点A在点B的左侧,与y轴负半轴交于点C,且
,点A在点B的左侧,与y轴负半轴交于点C,且![]() ,若点D是直线BC下方抛物线上一点,连接AD交BC于点E,记△ACE的面积为S1,△DCE的面积为S2,求
,若点D是直线BC下方抛物线上一点,连接AD交BC于点E,记△ACE的面积为S1,△DCE的面积为S2,求![]() 是否有最值?若有,求出该最值;若没有,请说明理由.
是否有最值?若有,求出该最值;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com