A. 平行四边形B. 矩形C. 菱形D. 正方形

（1）本次调查的学生共有 人，在扇形统计图中，m的值是 ；

（2）将条形统计图补充完整；

（3）在被调查的学生中，选修书法的有2名女同学，其余为男同学，现要从中随机抽取2名同学代表学校参加某社区组织的书法活动，请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率．

（1）求∠DBC的度数；

（2）求y关于x的函数解析式，并写出自变量x的取值范围；

（3）如图1，设点P、Q分别是边BC、AB的中点，分别联结OP，OQ，PQ．如果△OPQ是等腰三角形，求AD的长．

【题目】如图所示，，点E在CD上，EM和EN三等分，．①若，则__________；②当__________时，．

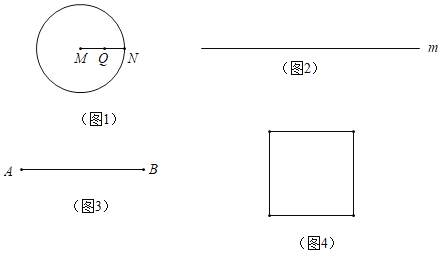
（概念认识）

已知点P和图形M，点B是图形M上任意一点，我们把线段PB长度的最小值叫做点P与图形M之间的距离．

例如，以点M为圆心，1cm为半径画圆如图1，那么点M到该圆的距离等于1cm；若点N是圆上一点，那么点N到该圆的距离等于0cm；连接MN，若点Q为线段MN中点，那么点Q到该圆的距离等于0.5cm，反过来，若点P到已知点M的距离等于1cm，那么满足条件的所有点P就构成了以点M为圆心，1cm为半径的圆．

（初步运用）

（1）如图2，若点P到已知直线m的距离等于1cm，请画出满足条件的所有点P．

（深入探究）

（2）如图3，若点P到已知线段的距离等于1cm，请画出满足条件的所有点P．

（3）如图4，若点P到已知正方形的距离等于1cm，请画出满足条件的所有点P．

【题目】小莉和她爸爸两人沿长江边扬子江步道匀速跑步，他们从渡江胜利纪念馆同时出发，终点是绿博园．已知小莉比她爸爸每步少跑，两人的运动手环记录时间和步数如下：

（1）表格中表示的结束时间为 ， ；

（2）小莉和她爸爸两人每步分别跑多少米？

（3）渡江胜利纪念馆到绿博园的路程是多少米？

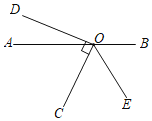
（1）若∠DOE＝150°，求∠AOC的度数．

（2）若∠DOE＝α，则∠AOC＝　 ．（请用含α的代数式表示）