
科目: 来源: 题型:
【题目】探究:数轴上任意两点之间的距离与这两点对应的数的关系.
![]()
(1)如果点A表示数5,将点A先向左移动4个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
如果点A表示数﹣2,将点A向右移动5个单位长度到达点B,那么点B表示的数是 ,A、B两点间的距离是 .
(2)发现:在数轴上,如果点M对应的数是m,点N对应的数是n,那么点M与点N之间的距离可表示为 (用m、n表示,且m≥n).
(3)应用:利用你发现的结论解决下列问题:数轴上表示x和﹣2的两点P与Q之间的距离是3,则x= .
查看答案和解析>>
科目: 来源: 题型:
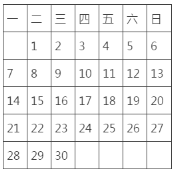
【题目】如图,是某年11月月历
(1)用一个正方形在表中随意框住4个数,把其中最小的记为![]() ,则另外三个可用含
,则另外三个可用含![]() 的式子表示出来,从小到大依次为____________,_____________,_______________.
的式子表示出来,从小到大依次为____________,_____________,_______________.
(2)在(1)中被框住的4个数之和等于76时,则被框住的4个数分别是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A,B,C处时,经测量得,甲船位于港口的北偏东43°45′方向,乙船位于港口的北偏东76°35′方向,丙船位于港口的北偏西43°45′方向.
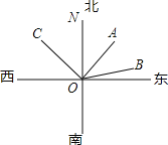
(1)求∠BOC的度数;
(2)求∠AOB的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】材料阅读
角是一种基本的几何图像,如图1角可以看作由一条射线绕着它的端点旋转而形成的图形.钟面上的时针与分针给我们以角的形象.如果把图2作为钟表的起始状态,对于一个任意时刻时针与分针的夹角度数可以用下面的方法确定.

因为时针绕钟面转一圈(![]() )需要12小时,所以时针每小时转过
)需要12小时,所以时针每小时转过![]() .
.
如图3中![]() 时针就转过
时针就转过![]() .
.
因为分针绕钟面转一圈(![]() )需要60分钟,所以分针每分钟转过
)需要60分钟,所以分针每分钟转过![]() .
.
如图4中![]() 分针就转过
分针就转过![]() .
.
再如图5中![]() 时针转过的度数为
时针转过的度数为![]() ,分针转过的度数记为
,分针转过的度数记为![]() ,此时,分针转过的度数大于时针转过的度数,所以
,此时,分针转过的度数大于时针转过的度数,所以![]() 时针与分针的夹角为
时针与分针的夹角为![]() .
.
知识应用
请使用上述方法,求出![]() 时针与分针的夹角.
时针与分针的夹角.
拓广探索
张老师某周六上午7点多去菜市场买菜,走时发现家中钟表时钟与分针的夹角是直角,买菜回到家发现钟表时针与分针的夹角还是直角,可以确定的是张老师家的钟表没有故障,走时正常,且回家时间还没到上午8点,请利用上述材料所建立数学模型列方程,求出张老师约7点多少分出门买菜?约7点多少分回到家?(结果用四舍五入法精确到分.)
查看答案和解析>>
科目: 来源: 题型:
【题目】小亮从家出发步行到公交站台后,等公交车去学校,如图, 折线表示这个过程中行程 s (千米)与所花时间 t (分)之间的关系,下 列说法错误的是( )
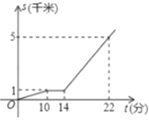
A.他家到公交车站台需行 1 千米B.他等公交车的时间为 4 分钟
C.公交车的速度是 500 米/分D.他步行与乘公交车行驶的平均速度300米/分钟
查看答案和解析>>
科目: 来源: 题型:
【题目】为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不超过200万元,又不低于198万元.开发建设办公室预算:一套A型“廉租房”的造价为5.2万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2)哪种建设方案投入资金最少?最少资金是多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年11月11日24时,天猫双11成交额达到2684亿元.同一天,各电商平台上众品牌网上促销如火如荼,纷纷推出多种销售玩法吸引顾客让利消费者.某品牌标价每件100元的商品就推出了如下的优惠促销活动
一次性购物总金额 | 优惠措施 |
少于或等于700元 | 一律打八折 |
超过700元,但不超过900元 | 一律打六折 |
超过900元 | 其中900元部分打五折, 超过900元的部分打三折优惠 |
(1)王教授一次性购买该商品12件,实际付款________元.
(2)李阿姨一次性购买该商品若干件,实际付款480元,请认真思考求出李阿姨购买该商品的件数的所有可能.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=100°,∠BCD=70°,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,求∠B的度数.

查看答案和解析>>
科目: 来源: 题型:
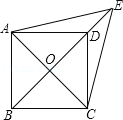
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,某公司员工住在![]() 三个住宅区,已知
三个住宅区,已知![]() 区有2人,
区有2人,![]() 区有7人,
区有7人,![]() 区有12人,三个住宅区在同一条直线上,且
区有12人,三个住宅区在同一条直线上,且![]() ,
,![]() 是
是![]() 的中点.为方便员工,公司计划开设通勤车免费接送员工上下班,但因为停车紧张,在
的中点.为方便员工,公司计划开设通勤车免费接送员工上下班,但因为停车紧张,在![]() 四处只能设一个通勤车停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠站应设在( )
四处只能设一个通勤车停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠站应设在( )
![]()
A.![]() 处B.
处B.![]() 处C.
处C.![]() 处D.
处D.![]() 处
处
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com