
科目: 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠B=30°,AC=3cm,点P在边AC上以1cm/s的速度从点A向终点C运动,与此同时点Q在边AB上以同样的速度从点B向终点A运动,各自到达终点后停止运动,设运动时间为t(s),则当△APQ是直角三角形时,t的值为( )
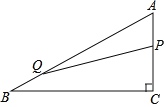
A.2sB.4sC.2s或4sD.2s或4.5s
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC=10cm,BC=12cm,D为BC上一点,连接AD,E为AD上一点,连接BE,若∠ABE=∠BAE═![]() ∠BAC,则DE的长为( )
∠BAC,则DE的长为( )

A.![]() cmB.
cmB.![]() cmC.
cmC.![]() cmD.1cm
cmD.1cm
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.

查看答案和解析>>
科目: 来源: 题型:
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A. 7.5平方千米 B. 15平方千米 C. 75平方千米 D. 750平方千米
查看答案和解析>>
科目: 来源: 题型:
【题目】(情境)某课外兴趣小组在一次折纸活动课中.折叠一张带有条格的长方形的纸片ABCD(如图1),将点B分别与点A,A1,A2,…,D重合,然后用笔分别描出每条折痕与对应条格线所在的直线的交点,用平滑的曲线顺次连结各交点,得到一条曲线.
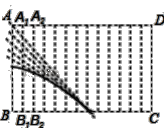
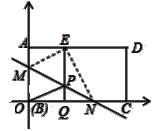
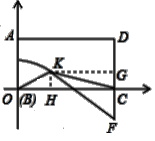
图1 图2 图3
(探索)(1)如图2,在平面直角坐标系xOy中,将矩形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB边放在y轴的正半轴上,AB=m,AD=n,(m≤n).将纸片折叠,使点B落在边AD上的点E处,过点E作EQ⊥BC于点Q,折痕MN所在直线与直线EQ相交于点P,连结OP.求证:四边形OMEP是菱形;
(归纳)(2)设点P坐标是(x,y),求y与x的函数关系式(用含m的代数式表示).
(运用)(3)将矩形纸片ABCD如图3放置,AB=8,AD=12,将纸片折叠,当点B与点D重合时,折痕与DC的延长线交于点F.试问在这条折叠曲线上是否存在点K,使得△KCF的面积是△KOC面积的![]() ?若存在,写出点K的坐标;若不存在,请说明理由.
?若存在,写出点K的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线l:y=﹣x2+bx+c(b,c为常数),其顶点E在正方形ABCD内或边上,已知点A(1,2),B(1,1),C(2,1).
(1)直接写出点D的坐标_____________;
(2)若l经过点B,C,求l的解析式;
(3)设l与x轴交于点M,N,当l的顶点E与点D重合时,求线段MN的值;当顶点E在正方形ABCD内或边上时,直接写出线段MN的取值范围;
(4)若l经过正方形ABCD的两个顶点,直接写出所有符合条件的c的值.

查看答案和解析>>
科目: 来源: 题型:
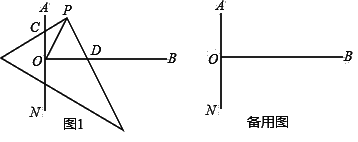
【题目】如图1,射线OB与直线AN垂直于点O,线段OP在∠AOB内,一块三角板的直角顶点与点P重合,两条直角边分别与AN、OB的交于点C、D.
(1)当∠POB=60°,∠OPC=30°,PC=2时,则PD= .
(2)若∠POB=45°,
①当PC与PO重合时,PC和PD之间的数量关系是 ;
②当PC与PO不重合时,猜想PC与PD之间的数量关系,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】数学是神秘奇妙的,数与字母有着密切的联系,字母可以表示数,数可以赋予字母其值,以下是某同学参加校庆举办的“越战越勇”活动的一道思考题,请同学们帮他完成,
(1)填表:
|
| |
用代数式表示 |
| |
|
| |
| ||
|
根据表中计算结果,你发现了什么等式?请写出这个等式
(2)利用(1)中发现的结论,计算![]()
查看答案和解析>>
科目: 来源: 题型:
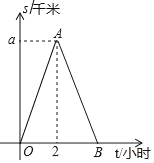
【题目】小明从家出发沿滨江路到外滩公园徒步锻炼,到外滩公园后立即沿原路返回,小明离开家的路程s(单位:千米)与走步时间t(单位:小时)之间的函数关系如图所示,其中从家到外滩公园的平均速度是4千米/时,根据图形提供的信息,解答下列问题:
(1)求图中的a值;
(2)若在距离小明家5千米处有一个地点C,小明从第一层经过点C到第二层经过点C,所用时间为1.75小时,求小明返回过程中,s与t的函数解析式,不必写出自变量的取值范围;
(3)在(2)的条件下,求小明从出发到回到家所用的时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】某水泥厂的仓库![]() 天内进出库的吨数记录如下(+表示进库,-表示出库):
天内进出库的吨数记录如下(+表示进库,-表示出库):![]()
(1)经过这![]() 天,水泥仓库里的水泥是增多了还是减少了?增多或减少了多少吨?
天,水泥仓库里的水泥是增多了还是减少了?增多或减少了多少吨?
(2)经过这![]() 天,水泥仓库管理员结算时发现还库存有
天,水泥仓库管理员结算时发现还库存有![]() 吨水泥,那么
吨水泥,那么![]() 天前水泥仓库里存有水泥多少吨?
天前水泥仓库里存有水泥多少吨?
(3)如果进仓库的水泥每吨运费为![]() 元,出仓库的水泥每吨运费为
元,出仓库的水泥每吨运费为![]() 元,那么这
元,那么这![]() 天共要付多少元运费?
天共要付多少元运费?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com