
科目: 来源: 题型:
【题目】数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.李明的作法如图所示,作线段AB使AB=C,以AB为直径作⊙O,以B为圆心,a为半径作弧交⊙O于点C,连接AC,△ABC即为所求作的三角形,你认为这种作法中判断∠ACB是直角的依据是( )
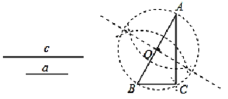
A. 90°的圆周角所对的弦是直径 B. 直径所对的圆周角是直角
C. 勾股定理的逆定理 D. 勾股定理
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是()
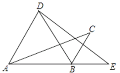
A. AD∥BC B. ∠CBE=∠C C. ∠ABD=∠E D. AD=BC
查看答案和解析>>
科目: 来源: 题型:
【题目】已知a,b为有理数,且a,b不为0,则定义有理数对(a,b)的“真诚值”为d(a,b)= ,如有理数对(3,2)的“真诚值”为d(3,2)=23﹣10=﹣2,有理数对(﹣2,5)的“真诚值”为d(﹣2,5)=(﹣2)5﹣10=﹣42.
,如有理数对(3,2)的“真诚值”为d(3,2)=23﹣10=﹣2,有理数对(﹣2,5)的“真诚值”为d(﹣2,5)=(﹣2)5﹣10=﹣42.
(1)求有理数对(﹣3,2)与(1,2)的“真诚值”;
(2)求证:有理数对(a,b)与(b,a)的“真诚值”相等;
(3)若(a,2)的“真诚值”的绝对值为|d(a,2)|,若|d(a,2)|=6,求a的值.
查看答案和解析>>
科目: 来源: 题型:
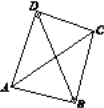
【题目】定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.
(1)如图,在损矩形ABCD中,∠ABC=∠ADC=90°,则该损矩形的直径是线段________.
(2)在损矩形ABCD内是否存在点O,使得A,B,C,D四个点都在以点O为圆心的同一个圆上?如果存在,请指出点O的具体位置.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知⊙O是等边三角形ABC的外接圆,P为劣弧BC上一点(点P与点B,C不重合).
(1)如果P是劣弧BC的中点,求证:PB+PC=PA;
(2)当点P在劣弧BC上移动时,(1)中的结论还成立吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,数轴上每相邻两点的相距一个单位长度,点A、B、C、D是这些点中的四个,且对应的位置如图所示,它们对应的数分别是a,b,c,d.
(1)当ab=﹣1,则d= .
(2)若|d﹣2a|=7,求点C对应的数.
(3)若abcd<0,a+b>0,化简|a﹣b|﹣|b+c﹣5|﹣|c﹣5|﹣|d﹣a|+|8﹣d|.
![]()
查看答案和解析>>
科目: 来源: 题型:
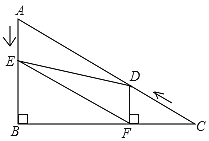
【题目】如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°,点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t(t>0)秒,过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:四边形AEFD是平行四边形;
(2)当t为何值时,△DEF是等边三角形?说明理由;
(3)当t为何值时,△DEF为直角三角形?(请直接写出t的值)
查看答案和解析>>
科目: 来源: 题型:
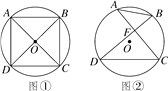
【题目】已知A,B,C,D是⊙O上的四个点.
(1)如图①,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;
(2)如图②,若AC⊥BD,垂足为F,AB=2,DC=4,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:若n=13,则第2018次“F”运算的结果是_____.
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:若n=13,则第2018次“F”运算的结果是_____.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】营养对促进中学生机体健康具有重要意义.现对一份学生快餐进行检测,得到以下信息:

根据上述信息回答下面的问题:
(1)这份快餐中蛋白质和脂肪的质量共 克;
(2)分别求出这份快餐中脂肪、矿物质的质量;
(3)学生每餐膳食中主要营养成分“理想比”为:碳水化合物:脂肪:蛋白质=8:1:9,同时三者含量为总质量的90%.试判断这份快餐中此三种成分所占百分比是否符合“理想比”?如果符合,直接写出这份快餐中碳水化合物、脂肪、蛋白质、矿物质的质量比;如果不符合,求出符合“理想比”的四种成分中脂肪、矿物质的质量(总质量仍为300克).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com